8.Формула Грина.

Сия очень полезная в сельском хозяйстве формула устанавливает связь между

криволинейными и двойными интегралами.

Пусть имеется некоторая правильная замкнутая область Д, ограниченная контуром L

и пущая ф-ции P(x,y) и Q(x,y) непрерывны вместе со своими частными

производными: 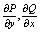в

данной области. тогда имеет место ф-ла:

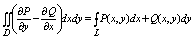
И вот вся эта фигулина и есть формула Грина.

Контур L определяющий область д может быть задан показательными уравнениями х =

х1(у), х=х2(у) с<=y<=d x1(y)<=x2(y) или

y = y1(x), y=y2(x) a<=x<=b y1(x)<=y2(x).

Рассмотрим область Д ограниченную неравенствами: a<=x<=b и

y1(x)<=y2(x). и преобразуем двойной интеграл

к криволинейным для чего сведем его к повторному и ф-ле Невтона-Лыебница

выполним интегрирование по у и получим:

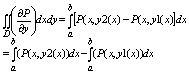каждый из 2 определенных интегралов в правой части последнего равенства = криволинейному

интегралу 2 рода взятому по соответствующей кривой а именно:

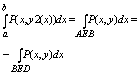
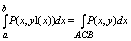
Итак двойной интеграл:

Формула Грина остается справедливой для всякой замкнутой области Д, которую

можно разбить проведением дополнительных линий на конечной число правильных

замкнутых областей.

9.Условия независимости криволинейного интеграла от пути интегрирования.

Криволинейный интеграл второго рода от векторной функции не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция , такая, что

В этом случае криволинейный интеграл второго рода от функции вдоль кривой C от точки A до точки B выражается формулой

(Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение

Векторное поле, обладающее свойством , называется потенциальным, а функция называется потенциалом.

10 Некоторые прил10ожения криволинейных интегралов.

Длина кривой

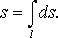     Масса кривой

( - плотность кривой).

     Координаты центра масс

     Работа

     Работа силы вдоль кривой l:

11-12.Поверхностные интегралы.

Определение поверхностного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая поверхность , на которой определена функция f(x,y,z). Разобьём поверхность на  частей , на каждой из частей  выберем произвольную точку , найдём  и площадь части  (которую будем обозначать тем же символом ), и составим интегральную сумму

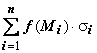
Поверхностный интеграл второго рода (по координатам).

  Определение поверхностного интеграла второго рода. Пусть в пространстве переменных x,y,z задана ограниченная кусочно-гладкая двусторонняя поверхность , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке  задана сторона поверхности), и на которой определена функция R(x,y,z). Разобьём поверхность на  частей , на каждой из частей  выберем произвольную точку , найдём , нормаль  в точке  к выбранной стороне поверхности, и площадь  проекции части  на плоскость ОХУ. В интегральную сумму слагаемое  возьмём со знаком "+", если  (т.е. если угол   между  и осью Oz - острый; проекция  на орт  оси Oz положительна), и со знаком "-", если . В результате интегральная сумма будет иметь вид .

14-15.Формулы Остроградского и Стокса.

  Формула Стокса

или в векторной форме

где единичный вектор нормали к поверхности S, направление которого таково, что при обходе контура l = дS поверхность S остается слева.      Формула Остроградского

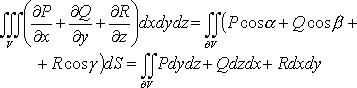
или в векторной форме

где дV = S - внешняя сторона поверхности, ограничивающей тело V; - единичный вектор внешней нормали к ней.