Теорема

Для любой функции  , аналитической в некоторой односвязной области   и для любой замкнутой кривой   справедливо соотношение 

[Править]Доказательство

Из условия аналитичности (уравнений Коши—Римана) следует, что дифференциальная форма   замкнута. Пусть теперь   — замкнутый самонепересекающийся кусочно-гладкий контур внутри области определения функции  , ограничивающий область  . Тогда по теореме Стокса имеем:

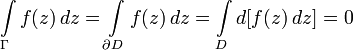
Производная функции комплексного переменного определяется, как и производная в действительной области: Здесь z₀, z ^_  комплексные и f(z₀) = f(z₀+z) - f(z).

Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.

1. Сумма и произведение дифференцируемых в точке функций,  есть функция и справедливы равенства:

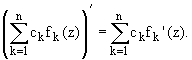
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :

3. Сложная функция f( (z)) дифференцируема в точке z₀, если в этой точке дифференцируема функция  (z), а функция f(u) дифференцируема в точке u₀, где u₀ =  (z₀) и u =  (z). При этом в точке z₀ имеет место формула:

Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.  Например, рассмотрим функцию  f(z) = z³. По определению производной для любой точки z, принадлежащей комплексной области, записываем:

Предел существует для любой точки z, принадлежащей комплексной области и (z³)' =3z². Аналогично можно получить: (zⁿ)' = nzⁿ-1 (n - действительное число).

24. Аналитическая функция комплексной переменной

Аналитическая функция (комплексного переменного) — функция комплексного переменного   (где   и   — вещественнозначные функции комплексного переменного, являющиеся, соответственно, вещественной и мнимой частью рассматриваемой функции), для которой в каждой точке некоторой области  , называемой областью аналитичности, выполняется одно из трёх равносильных условий:

1. Для вещественной и мнимой части этой функции в каждой точке 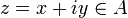  выполняются условия Коши — Римана (аналитичность в смысле Коши — Римана);

2. Ряд Тейлора функции в каждой точке 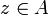  сходится и его сумма равна   (аналитичность в смысле Вейерштрасса);

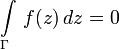3. Интеграл   для любой замкнутой кривой   (аналитичность в смысле Коши)

25. Понятие конформного отображения

Взаимно однозначное отображение области D на область D^* (евклидова пространства или риманова многообразия) называется конформным (лат. conformis — подобный), если в окрестности любой точки D дифференциал этого преобразования есть композиция ортогонального преобразования и гомотетии.

Этот термин пришёл из комплексного анализа, изначально использовался только для конформных отображений областей плоскости.

Свойства

Пример конформного отображения. Видно, что перпендикулярность сохраняется.

• Конформное отображение сохраняет форму бесконечно малых фигур;

• Конформное отображение сохраняет углы между кривыми в точках их пересечения (свойство сохранения углов).

  • Это свойство можно также взять за определение конформного отображения.

• Теорема Лиувилля: Всякое конформное отображение области евклидова пространства 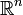  при   можно представить в виде конечного числа суперпозиций — изометрий и инверсий.

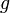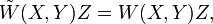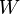• Кривизна Вейля сохраняется при конформном отображении, то есть если   и   — конформноэквивалентные метрические тензоры, то      где   и   обозначают тензоры Вейля для   и   соответственно.

• Для конформно-эквивалентых метрик 

  • Связности связаны следующей формулой:    

  • Кривизны связаны следующей формулой:           если   а   обозначает Гессиан функции  .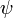

  • Формулу для секционных кривизн можно записать в следующем ви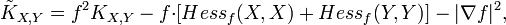де:      где  .

  • При вычислении скалярной кривизны 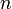 -мерного риманова многообразия, удобнее записывать конформный фактор в виде  . В этом случае:

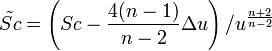
26. Понятие интеграла функции комплексного переменного и его свойства

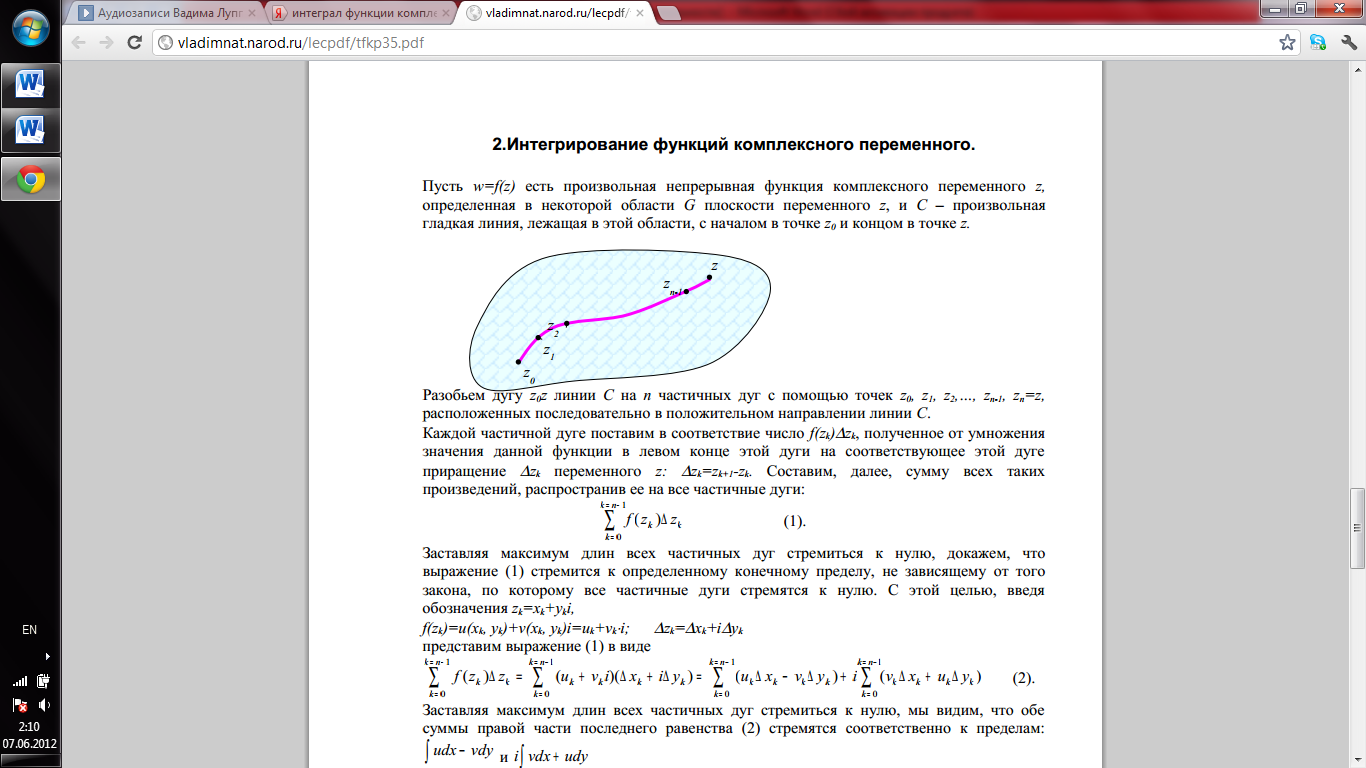
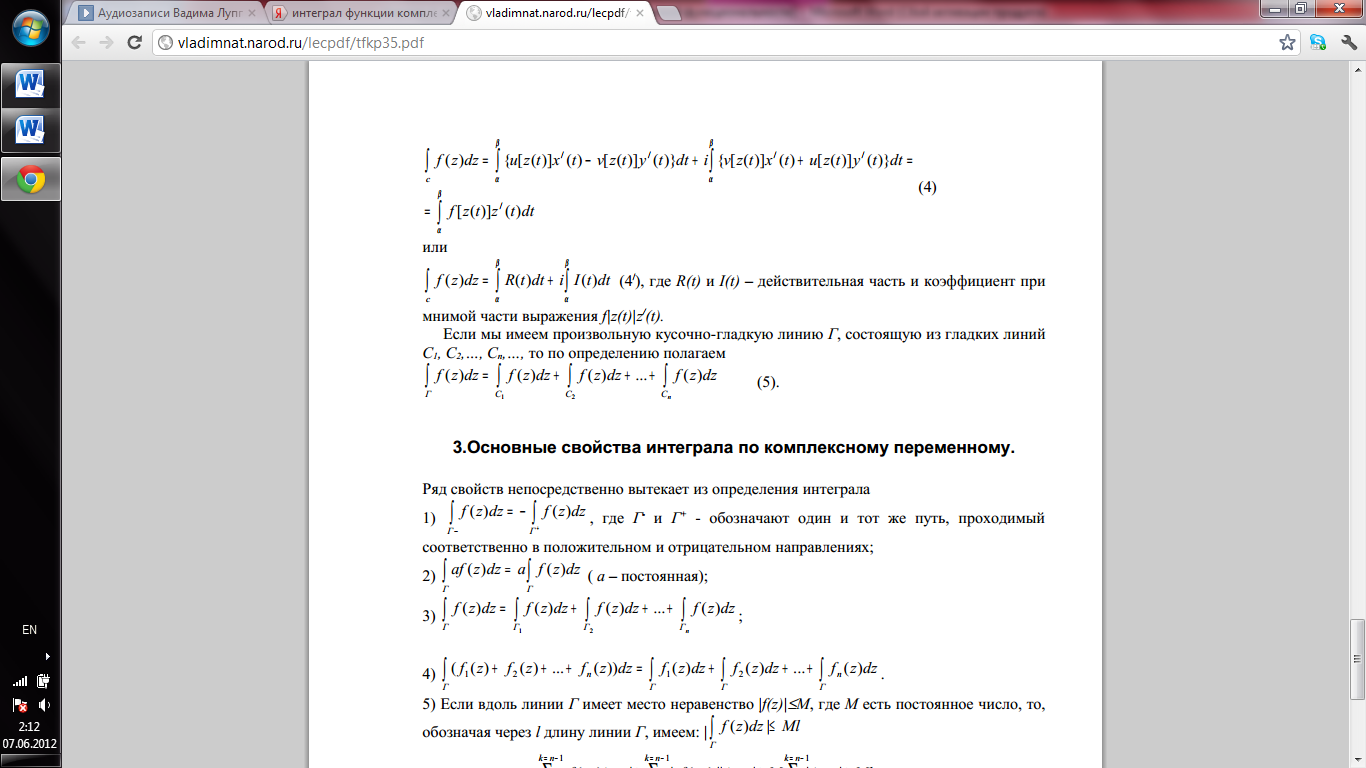
27. Теорема Коши для односвязной и многосвязной области.

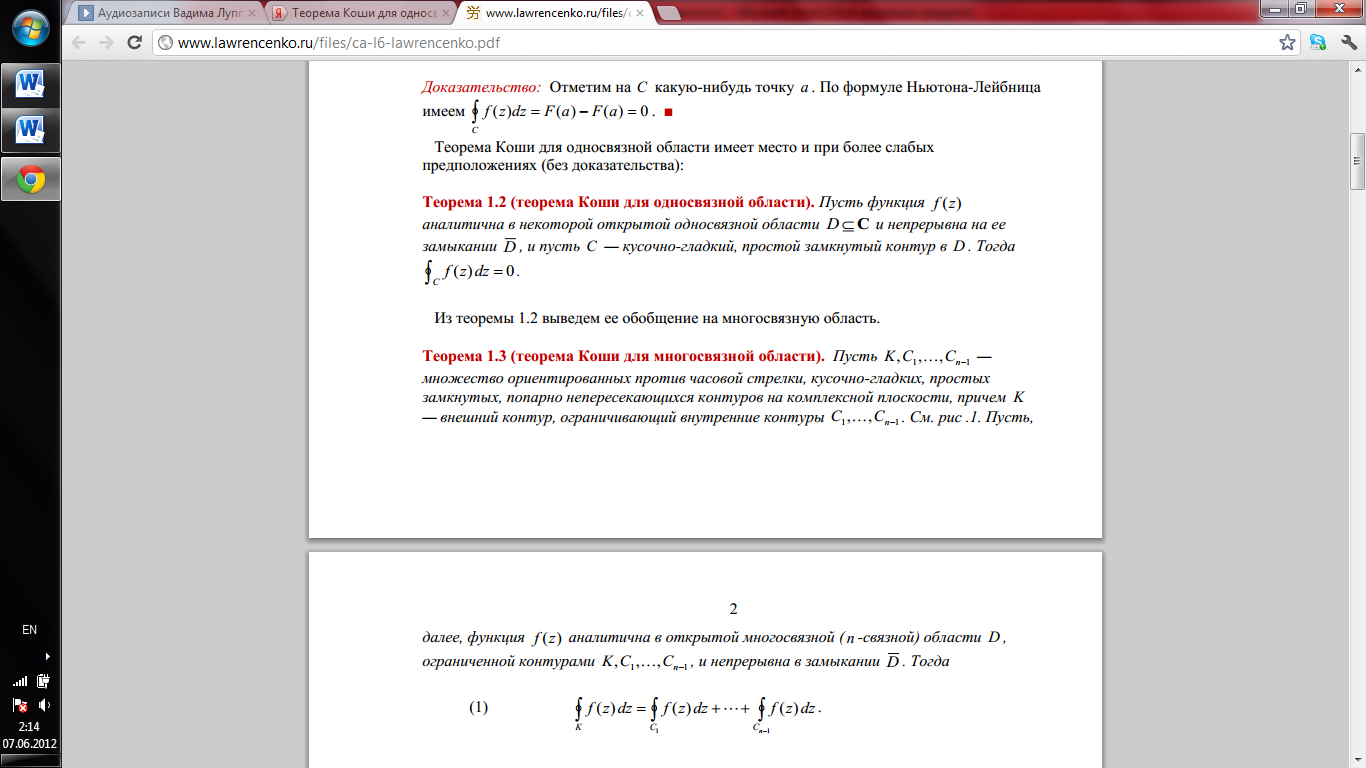
28. Первообразная функции комплексной переменной. Формула Ньютона-Лейбница.

Пусть функция f (z) – определена и непрерывна в области G, а G – кусочно-гладкая кривая, лежащая в области G; z=x+iy, f(z)=u+iv, где u=u(x,y), v=v(x,y) – действительные функции переменных x и y. Вычисление интеграла от функции w=f(z) сводится к вычислению криволинейных интегралов второго рода

Если кривая задана параметрическими уравнениями x=x(t), y=y(t), а начальная и конечная точки дуги соответствуют значениям t=, t=, то

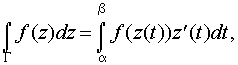
где z(t)=x(t)+iy(t).

Пусть Г – кусочно-гладкая кривая, состоящая из гладких частей Г₁, Г₂...Г_n. Тогда

Равенство

Ньютон лейбниц

Если   непрерывна на отрезке   и   — ее любая первообразная на этом отрезке, то имеет место Равенство

29. Интегральная формула Коши.