Исследовать возможность улучшения обусловленности задачи посредством внесения малого случайного возмущения в матрицу системы.
M-возмущение:
-
Поря-
док
Но-
мер
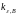
cond
Real Error
ErrEst(cond)
5
3
0
0
1.000E+0001
3.436E-0012
1.93E-0011
1.00E+0000
0
1.000E+0001
3.436E-0012
1.93E-0011
1.00E+0007
0
1.000E+0001
2.021E-0012
1.44E-0011
1.00E+0012
0
1.000E+0001
8.229E-0008
5.16E-0012
1.00E+0016
0
9.999E+0000
3.403E-0004
6.41E-0012
0
1.00E+0000
1.000E+0001
3.436E-0012
1.93E-0011
0
1.00E+0004
1.000E+0001
3.436E-0012
1.93E-0011
0
1.00E+0012
1.000E+0001
1.084E-0007
1.08E-0006
0
1.00E+0016
1.000E+0001
1.084E-0003
1.08E-0002
1.00E+0002
1.00E+0002
1.000E+0001
1.617E-0012
8.94E-0012
1.00E+0003
1.00E+0003
1.000E+0001
1.617E-0012
8.94E-0012
1.00E+0002
1.00E+0003
1.000E+0001
1.617E-0012
8.94E-0012
1.00E+0003
1.00E+0001
1.000E+0001
1.617E-0012
8.94E-0012
1.00E+0016
1.00E+0016
1.000E+0001
1.326E-0003
1.08E-0002
5
11
0
0
4.837E+0007
4.834E-0006
2.72E-0005
1.00E+0002
0
4.837E+0007
4.834E-0006
2.72E-0005
1.00E+0007
0
4.837E+0007
4.834E-0006
2.72E-0005
1.00E+0012
0
4.885E+0007
2.600E-0001
2.14E-0005
1.00E+0016
0
2.976E+0004
5.905E+000
6.14E-0008
0
1.00E+0002
4.837E+0007
4.834E-0006
2.72E-0005
0
1.00E+0005
4.837E+0007
4.834E-0006
2.72E-0005
0
1.00E+0012
4.837E+0007
1.144E-0005
5.24E+0000
0
1.00E+0016
1.000E+0001
1.084E-0003
5.24E+0004
1.00E+0002
1.00E+0004
4.837E+0007
6.919E-0006
1.60E-0005
1.00E+0005
1.00E+0002
4.837E+0007
6.919E-0006
1.60E-0005
1.00E+0006
1.00E+0001
4.837E+0007
6.919E-0006
1.60E-0005
1.00E+0005
1.00E+0005
1.000E+0001
6.919E-0006
1.60E-0005
1.00E+0008
1.00E+0008
1.000E+0001
2.227E-0005
5.40E-0004
1.00E+0016
1.00E+0016
6.659E+0004
1.088E+001
7.22E+0001
Для хорошо
обусловленных задач внесение возмущения
влияет на обусловленность (не беря во
внимание аномально большие возмущения
порядка
,
при которых возрастает и ошибка, и
обусловленность).
Для задач с плохой обусловленностью
внесение возмущения внесение возмущения
может улучшить обусловленность задачи,
но при этом может увеличиться и ошибка
решения. Поэтому допустимо пользоваться
внесением возмущения для улучшения
обусловленности плохо обусловленных
задач, но нужно подбирать оптимальное
возмущение. Следует
отметить также, что оценка ErrEst(cond) в
некоторых случаях даёт сильно заниженный
результат по сравнению с реальной
ошибкой.
6 Для
2-3 задач с «хорошей» матрицей (mm
= 102
-
104
) посредством внесения в матрицу системы
возмущений различной величины сделать
заключение о приемлемой для получения
требуемой (наперед заданной) точности
решения степени неопределенности в
задании исходных данных.
Р-возмущение:
-
Поря-
док
Но-
мер
cond
Real Error
ErrEst(cond)
5
3
0
0
1.000E+0001
3.092E-0012
3.86E-0012
1.00E+0002
0
1.000E+0001
3.092E-0012
3.86E-0012
1.00E+0006
0
1.000E+0001
3.092E-0012
3.99E-0012
1.00E+0012
0
1.000E+0001
8.229E-0008
5.16E-0012
1.00E+0016
0
9.999E+0000
3.403E-0004
6.41E-0012
0
1.000E+0002
1.000E+0001
3.092E-0012
3.86E-0012
0
1.000E+0003
1.000E+0001
3.092E-0012
3.86E-0012
0
1.000E+0012
1.000E+0001
1.084E-0007
1.08E-0006
0
1.000E+0016
1.000E+0001
1.084E-0003
1.08E-0002
1.00E+0002
1.000E+0005
1.000E+0001
4.366E-0012
3.97E-0012
1.00E+0005
1.000E+0004
1.000E+0001
4.366E-0012
3.96E-0012
1.00E+0016
1.000E+0016
1.000E+0001
1.764E-0003
1.08E-0002
Для хорошо
обусловленной задачи внесение возмущения
лишь увеличивает ошибку (не улучшая при
этом обусловленности). Точность решения
даже при внесении очень больших возмущений
не поднималась выше
.
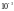Также из полученных данных следует, что
оценка ошибки ErrEst(cond)
сильно занижена по сравнению с реальной
ошибкой.