9. Отношение. Бинарное отношение. Рефлексивное, симметричное, антисимметричное, асимметричное, транзитивное отношения.

Отношение - произвольное подмножество R множества Aⁿ всех кортежей (упорядоченных наборов) вида a₁,...,a_n), где a₁,...,a_n -элементы некоторого множества A; в этом случае говорят, что R есть n-местное отношение на A. Понятие отношения служит в математике для выражения на теоретико-множественном языке связей между объектами. Множество всех таких элементов a, которые входят хотя бы в один кортеж, принадлежащий отношению R называется полем этого отношения. Двухместные отношения называются бинарными. Если R - бинарное отношение, то вместо  a, b R, часто пишут aRb. Частным случаем понятия отношения является соответствие.

Через обозначается отношение принадлежности, т.е. x  A означает, что элемент x принадлежит множеству A.

Если x не является элементом множества A, то это записывается x  A.

Два множества A и B считаются равными, если они состоят из одних и тех же элементов. Пишется A = B, если A и B равны, и A ╧  B в противном случае.

Через  обозначается отношение включения множеств, т.е. A  B означает, что каждый элемент множества A является элементом множества B. В этом случае A называется подмножествомB, а B - надмножествомA. Если A  B и A ╧ B, то A называется собственным подмножеством B, и в этом случае пишем A  B.

1. Унарные:

2. Бинарные:

M, aRb

3. Соответствия a, b, r

4. n-местные отношения

Пусть R Í A ´ A. Соответствие R называется:

• рефлексивным, если для

• антирефлексивным (для )

• симметричным, если

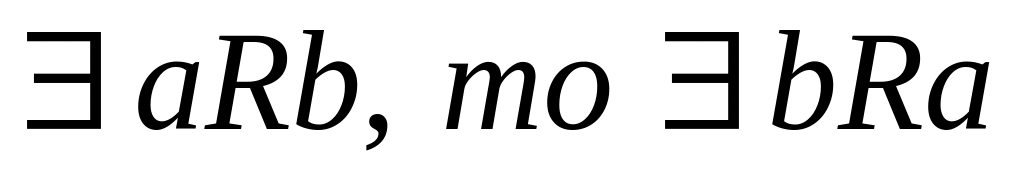
• антисимметричным, если

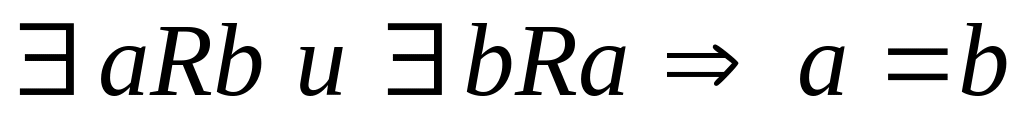
• асимметричным, если R Ç R#  = Æ;

• транзитивным, если

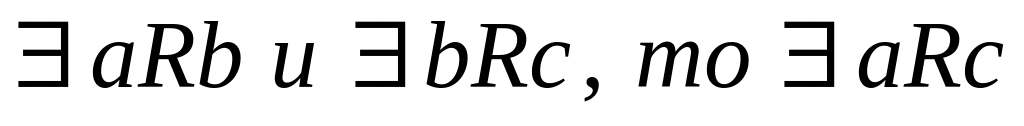
Отношение R называется:

a) эквивалентностью, если оно рефлексивно, симметрично и транзитивно

b) толерантностью, если оно рефлексивно и симметрично;

c) предпорядком, если оно рефлексивно и транзитивно;

d) порядком, если оно транзитивно и антисимметрично.

10. Отношение эквивалентности. Фактор-множество множества по отношению.

Если R —  эквивалентность, то множество A распадается на непересекающиеся классы эквивалентных элементов, или на классы эквивалентности. Множество классов эквивалентности называется фактор-множеством множества A по отношению R. Число классов эквивалентности отношения эквивалентности R называют индексом множества A.

Подмножество называется местным ( мерным) отношением на множестве А. Говорят, что элементы находятся в отношении , если .

Наиболее часто встречающимися и хорошо изученными являются двухместные или бинарные отношения.

Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.

Отношение называется рефлексивным, если для любого элемента имеет место .

Главная диагональ матрицы рефлексивного отношения содержит только единицы.

Отношение называется симметричным, если для любой пары из отношения следует . Иными словами, отношение является симметричным тогда и только тогда, когда для любой пары оно выполняется в обе стороны (или вовсе не выполняется).

Матрица симметричного отношения симметрична относительно главной диагонали: для любых .

Отношение называется транзитивным, если для любых из отношений и следует (R²  R)

Пусть на множестве задано отношение эквивалентности . Осуществим следующее построение. Выберем элемент и образуем класс (подмножество ), состоящий из элемента и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент и образуем класс , состоящий из и эквивалентных ему элементов. Продолжая эти действия, получим систему классов (возможно, бесконечную) такую, что любой элемент из множества входит хотя бы в один класс, то есть .

Эта система обладает следующими свойствами: она образует разбиение множества , то есть классы попарно не пересекаются; любые два элемента из одного класса эквивалентны; любые два элемента из разных классов не эквивалентны.

Все эти свойства прямо следуют из определения отношения эквивалентности. Действительно, если бы, например, классы и пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен и . Тогда, в силу транзитивности отношения выполнялось бы . Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.