3 Квадратичная форма. Приведение к каноническому виду
3.1 Основные определения. Матрица квадратичной формы
Пусть
,
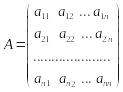где
,
– симметричная матрица порядка n,
и пусть
.
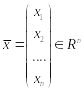Рассмотрим числовую функцию
,
аргументом которой является вектор
,
обозначим эту функцию
.
Запишем
в координатном виде:
,
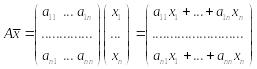i-я координата полученного вектора равна
.
Умножим полученный вектор скалярно на вектор , получим :
,
,
.
(*)
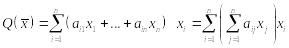Определение. Скалярная
функция векторного аргумента
,
где А – симметричная матрица порядка
n,
,
называется квадратичной формой, а
матрица А – матрицей квадратичной
формы.
Выражение (*) является координатной записью квадратичной формы.
Пример 1. Записать в координатном виде квадратичную форму c матрицей
,
,
,
.
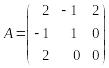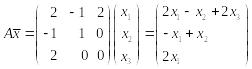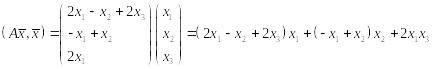Вообще говоря, квадратичную форму по
ее матрице выписывают без промежуточных
вычислений: элементы главной
диагонали матрицы являются коэффициентами
при квадратах переменных; элемент
– есть коэффициент при произведении ,
и ввиду симметричности матрицы А:
,
а потому в
коэффициент при произведении
равен
.
Можно решить и обратную задачу: по данной квадратичной форме выписать ее матрицу.
Пример 2. Выписать матрицу квадратичной формы
.
;
;
(коэффициенты при
и
.
).
(коэффициенты при
и
).
(коэффициенты при
и
).
(коэффициенты при
и
),
итак
.
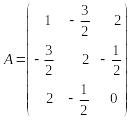Итак, квадратичная форма
,
является многочленом второй степени
от n переменных, не содержащем
свободного члена и членов первой степени;
причем, подобные
и
таковы, что
.
Каждая симметричная матрица определяет некоторую квадратичную форму и обратно: каждой квадратичной форме ставится в соответствие ее симметричная матрица.
Квадратичная форма – функция координат вектора , а значит ее вид зависит от базиса в , в котором задан вектор .
3.2 Преобразование матрицы при линейной замене переменных
В этом параграфе мы рассмотрим, как
преобразуется матрица А квадратичной
формы
при переходе из одного базиса к другому.
Напомним, что замена одного базиса другим задается матрицей перехода С, столбцы которой есть координаты “нового” базиса по “старому”. При этом координаты произвольного вектора: меняются следующим образом:
,
где
– вектор-столбец “старых” координат, а – вектор-столбец “новых” координат.
Запишем эту замену переменных:
,
(*)
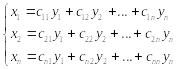здесь переменные
представлены как линейные функции
(точнее, линейные формы) от новых
переменных
.
Подставляя выражение (*) в квадратичную
форму
,
мы получим новую квадратичную форму,
зависящую от переменных
с матрицей В:
.
Нас интересует связь между матрицами А и В.
Формулы (*) задают линейное
преобразование, сопоставляющее
каждому вектору
вектор
.
Матрицу С называют матрицей
линейного преобразования. В
нашем случае это матрица перехода,
следовательно невырождена, и тогда
осуществляет обратное линейное
преобразование
.
Итак, как меняется матрица квадратичной формы при линейном преобразовании ?
Теорема. При линейной замене переменных квадратичная форма переходит в квадратичную форму
,
где матрицы А и В связаны соотношением:
,
где
– транспонированная матрица С.
Наша дальнейшая цель состоит в том, чтобы путем перехода к переменным получить квадратичную форму более простого вида.