Тематический обзор*

1 Собственные числа и собственные векторы матрицы

1.1 Определение. Основные свойства собственных векторов

В первой части нашего курса линейной алгебры (юнита 1) мы рассмотрели операцию умножения матрицы А на вектор , результатом которой является новый вектор .

Так, например,

.

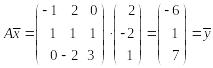Вектор под действием матрицы А преобразуется в новый вектор . В этом преобразовании вектор считается образом вектора , а – прообразом вектора . Особую роль для матрицы А играют те векторы , образы которых коллинеарны своим прообразам.

Пусть А квадратная матрица порядка n.

Определение. Вектор называется собственным вектором матрицы А, если обладает следующими свойствами:

1) ;

2) существует такое число , что , т.е. .

При этом, число называется собственным числом, или собственным значением матрицы А.

Говорят, что собственный вектор соответствует (отвечает) собственному значению матрицы А. Задача об отыскании собственных векторов и собственных значений матрицы (преобразования) А имеет много важных приложений. Чем больше собственных векторов матрицы мы знаем, тем лучше понимаем, как действует матрица (преобразование) А на вектор .

Рассмотрим несколько примеров.

1. А=Е, где

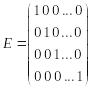– единичная матрица.

Тогда , для любого вектора . Следовательно, любой вектор есть собственный вектор Е, отвечающий собственному значению .

2.

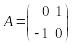
Проверим, как преобразует матрица А вектора базиса и .

; .

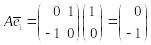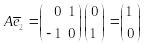Очевидно, векторы базиса при умножении на матрицу А поворачиваются на угол по часовой стрелке. Матрица А осуществляет поворот каждого вектора на угол по часовой стрелке (рисунок 1, 2, 3).

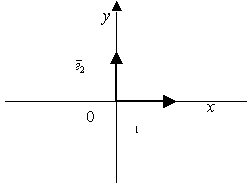
Рисунок 1

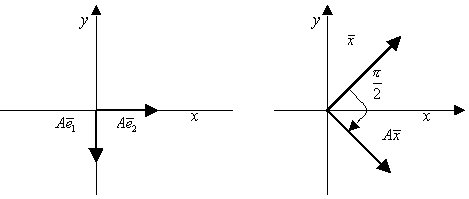
Рисунок 2 Рисунок 3

Из геометрических соображений ясно, что при таком преобразовании никакой вектор не переходит в коллинеарный себе.

Действительно, если собственный, то

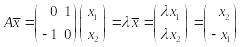, т.е.

,

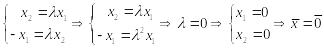т.е. вектор не может быть собственным; матрица А собственных векторов не имеет.

Отметим некоторые свойства собственных векторов матрицы А.

1. Векторы, отвечающие данному собственному числу , образуют подпространство (собственное подпространство). Напомним, что множество является подпространством , если линейные операции над векторами не выводят вектор из V.

Действительно, пусть – собственные векторы матрицы А, отвечающие собственному значению , т.е. .

Тогда .

Таким образом, каждому собственному числу соответствует бесчисленное множество коллинеарных собственных векторов, образующих подпространство , которое называют собственным подпространством матрицы А (хотя не входит во множество ).

О свойствах собственных подпространств, (о размерности) будет сказано ниже.

2. Собственные векторы, соответствующие различным собственным числам, линейно независимы.

Проверим это утверждение для двух векторов.

Пусть собственные векторы матрицы А, соответствующие собственным числам , пусть , тогда линейно независимы (не коллинеарны). Предположим противное, пусть . Умножим последнее равенство на А:

.

Так как, , то , что противоречит условию, т.е. наше предположение неверно и линейно независимы.

По индукции можно доказать, что если – различные собственные числа, то соответствующие им собственные векторы линейно независимы (m – любое целое число).