Вопрос 2: Уравнения теплоемкостей в изотермическом, изобарном, изохорном, адиабатном и политропных процессах.

Работой можно назвать термодинамический процесс совершаемый системой над внешними телами. dA=dpdV

Для перевода системы из одного состояния в другое с помощью различных термодинамических процессов , ей нужно сообщать определенное количество теплоты.

Теплота и работа являются функциями изменения системы.

Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты Q, полученного телом, к соответствующему приращению его температуры T:

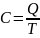(1)

Единица измерения теплоёмкости в системе СИ — Дж/К.

Теплоемкость зависит от массы тела, его химического состава, термодинамических составляющих и процесса сообщения теплоты термодинамической системы. 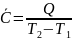при Т₂ Т₁ (2)

Связь между (1) и (2): 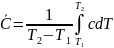(3)

Удельная теплоемкость: С=с/М

Для смеси N газов:

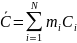
Молярной (мольной) называется: 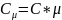, где 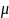- молярная масса.

Элементарное количество теплоты, сообщаемое газом для его температуры от Т до Т+dT или dq=cdT.

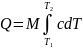
1 закон ТЕРМОДИНАМИКИ:

Количество теплоты, сообщаемое системе расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил.

dQ=dV+dA; dQ=dV+pdV.

cdT=dU+pdV (1)

Если на систему равномерно распределяется внешнее давление и действуют другие силы, то:

cdT=dU+pdV+dR.

Изохо́рная теплоёмкость — теплоёмкость тела при изохорическом процессе.

, где γ — показатель адиабаты, R — универсальная газовая постоянная.

А при постоянном давлении (изобарная теплоемкость):

R = 8.31 Дж/(моль К) — универсальная газовая постоянная.

i – Количество степеней свободы.

При изохорном: (dv/dt)=0; U=Mf (T)

При изобарном: (dv/dt)=M / * R/p

Уравнение Майера:

С_p – С_v = M / * R

C_pM – C_VM = R

Из инета:

МАЙЕРА УРАВНЕНИЕ

- ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении Cp и пост, объёме С _V 1 кмоля идеального газа:  где R- газовая постоянная. Впервые было получено Ю. P. Майером (J. R. Mayer) в 1842 и ещё до работ Дж. П. Джоуля (J. P. Joule) использовано им для количеств, определения механического эквивалента теплоты. Для произвольной массы т (кг) вещества в состоянии идеального газа M. у. записывается в виде:   , где  - молекулярная масса газа. M. у. можно получить из общего соотношения   (см. Термодинамика), если учесть, что для идеального газа справедливо Клапейрона уравнение.

В термодинамике используют так называемый термодинамический коэффициент адиабаты:

С_V = R / K-1 * M / ;

C_VM = R / K-1 ;

C_V = R / (K-1)*M

Билет 3

43.Уравнения изменений энтальпии в изотермическом, изобарном, изохорном, адиабатном и политропных процессах.

1.Изотермический:

2.Изобарный:

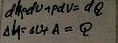
3.Изохорный: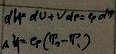

4.Адиабатный:

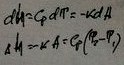
5.Политрропный:

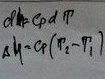
2 вопрос

3.Основные характеристики движения жидкости. Гидравлический радиус и эквивалентный диаметр.

Рассмотрим движение жидкости по трубе постоянного сечения.Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называют расходом жидкости. Различают объемный расход (м³/с, м³/ч) и массовый расход (кг/ч, кг/с).

В разных точках поперечного сечения потока скорость частиц жидкости неодинакова.

В расчетах обычно используют среднюю скорость  (м/с): 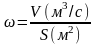. (2.28)

Массовый расход М (кг/с): M =    S , (2.29)

где  – плотность;  – массовая скорость, W = .

Приведенные основные характеристики движения жидкостей относятся к их перемещению в каналах с сечением любой формы.

Гидравлический радиус и эквивалентный диаметр

При движении жидкости через площадь поперечного сечения любой формы, отличной от круглой, в качестве расчетного линейного размера принимают гидравлический радиус, или эквивалентный диаметр.

Гидравлический радиус r_r (м) – это отношение площади свободного сечения трубопровода или канала, через которое протекает жидкость, к смоченному периметру, т.е. 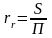, (2.30)

где S – площадь сечения потока жидкости, м; П – смоченный периметр, м.

Для круглой трубы диаметром d получаем , , .

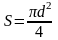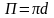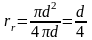Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр: d = d_э = 4r_r.

Таким образом, d_э = 4S/П . (2.31)

Эквивалентный диаметр d_э равен диаметру гипотетического трубопровода круглого сечения, для которого отношения площади S к смоченному периметру П то же, что и для трубопровода некруглого сечения.

Для канала прямоугольного сечения со сторонами a и b, полностью заполненного жидкостью, гидравлический радиус равен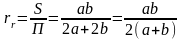 , а эквивалентный диаметр составляет .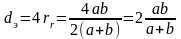

Для канала кольцевого поперечного сечения, в котором жидкость ограничена внутренней и наружной окружностями с диаметрами d_в и d_н соответственно, эквивалентный диаметр определяется как

.

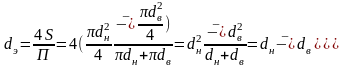Для круглой трубы d_э=d.

Билет 4