Основное уравнение гидростатики

Из уравнений (2.11) следует, что давление в покоящейся жидкости изменяется только по вертикали (вдоль оси Z), оставаясь одинаковым во всех точках любой горизонтальной плоскости, так как изменения давления вдоль осей X и Y равны нулю.

В связи с тем, что в этой системе уравнений частные производные 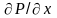и 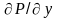равны нулю, частная производная 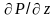может быть заменена на , и следовательно, .

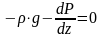Отсюда получаем:

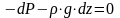. (2.12)

Разделив левую и правую части (2.12) на g и переменив знаки, представим (2.12) в виде:

.

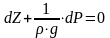Для несжимаемой однородной жидкости плотность постоянна, и следовательно,

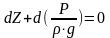
или

.

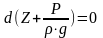После интегрирования получим:

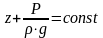. (2.13)

Для двух произвольных горизонтальных плоскостей 1 и 2 уравнение (2.13) выражают в форме:

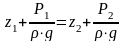. (2.14)

Уравнения (2.13) и (2.14) являются основными уравнениями гидростатики. В уравнении гидростатики (2.14): Z₁ и Z₂ - высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), a P₁ и P₂ - гидростатические давления в этих точках.

Рассмотрим, например, две частицы жидкости, из которых одна расположена в точке 1 внутри объема жидкости (см. рисунок 2.3) на высоте Z от произвольно выбранной плоскости сравнения 0-0, а другая находится в точке 2 на поверхности жидкости (на высоте Z₀ от той же плоскости).

Пусть Р и Р₀ - давления в точках 1 и 2 соответственно. При этих

обозначениях согласно уравнению (2.14) получим:

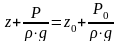(2.15)

или

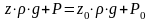. (2.16)

Член Z в уравнении гидростатики, представляющий собой высоту расположения данной точки под произвольно выбранной плоскостью сравнения, называется нивелирной высотой и выражается в единицах длины.

Величину 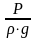называют статическим или пьезометрическим напором.

Следовательно, согласно основному уравнению гидростатики для каждой точки покоящейся жидкости сумма нивелирной высоты и статического напора есть величина постоянная.

Нивелирную высоту называют геометрическим напором, характеризующим удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения, а статический напор – удельной потенциальной энергией давления в этой точке.

Основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.

Уравнение (2.15) можно записать в форме:

(2.17)

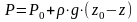или . (2.18)

Уравнение (2.18) является выражением закона Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема.

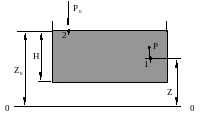
Рисунок 2.3 - К основному уравнению гидростатики