
- •Билет №1
- •Вопрос 1: Показатель политропы в изотермическом, изобарном, изохорном, адиабатном и политропных процессах.
- •Показатель политропы:
- •Вопрос 2: Законы гидрогазодинамики. Физические свойства жидкостей (газов).
- •Билет №2
- •Вопрос 1: Дифференциальное уравнение равновесия Эйлера (вывод). Основное уравнение гидростатики. Дифференциальные уравнения равновесия Эйлера
- •После преобразования находим:
- •Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:
- •Основное уравнение гидростатики
- •Вопрос 2: Уравнения теплоемкостей в изотермическом, изобарном, изохорном, адиабатном и политропных процессах.
- •43.Уравнения изменений энтальпии в изотермическом, изобарном, изохорном, адиабатном и политропных процессах.
- •3.Основные характеристики движения жидкости. Гидравлический радиус и эквивалентный диаметр.
- •4.Дифференциальное уравнение для установившегося и неустановившегося потока.
- •42.Уравнения изменений внутренней энергии в изотермическом, изобарном, изохорном, адиабатном и политропных процессах.
- •5.Режимы движения жидкостей и расход жидкости при ламинарном движении потока.
- •41.Уравнения количества теплоты, сообщаемое в адиабатном и политропном процессах.
- •6.Дифференциальное уравнение неразрывности потока. Практическое приложение.
- •Вопрос 2
- •Работа при адиабатическом процессе
- •Расчёт теплоты и работы политропных процессов сжатия газов
- •Вопрос 7
- •7. Дифференциальное уравнение движения идеальной жидкости (уравнение эйлера).
- •Вопрос 2
- •9.Вывод уравнения Бернулли. Практическое применение.
- •9.Вывод уравнения Бернулли. Практическое применение.
- •Вопрос 2
- •10.Теория подобия – метод научного обобщения экспериментов.
- •Вопрос 2
- •11. Условия и теория подобия.
- •Вопрос 2
- •36.Простейшие термодинамические процессы идеальных газов.
- •4Адиабатный процесс
- •5. Политропный процесс
- •Вопрос 13
- •12. Первая теорема подобия. Преобразование дифференциального уравнения в критериальное. Подобие начальных и граничных условий
- •Вопрос 2
- •35.Параметр состояния термодинамической системы – энтропия. Вывод.
- •13. Вторая теорема подобия. Пример использования.
- •Вопрос 2
- •34. Второй закон термодинамики. Основные постулаты, вытекающие изз второго закона термодинамики.
- •14. Третья теорема подобия. Раскрыть ее сущность.
- •Вопрос 2
- •33.Уравнение Майера.
- •Вопрос 16
- •15. Преобразование дифференциального уравнения Навье-Стокса в критериальное. Гидравлическое подобие
- •Для установившегося потока
- •Вопрос 2
- •32.Первый закон термодинамики. Раскрыть сущность.
- •16. Модифицированные и производные критерии подобия
- •Вопрос 2
- •30.Работа и теплота
- •28. Внутренняя энергия системы. Внутренняя энергия идеального газа.
- •29. Энтальпия идеального газа.
- •19. Гидравлическое сопротивление при движении жидкостей (газов) в трубах и каналах.
- •26. Смеси идеальных газов. Массовая и молярная концентрация. Парциальное давление. Закон Дальтона.
- •21. Сопротивление при свободном движении тел в газах и жидкостях
- •22. Осаждение частиц под действием сил тяжести и инерции. Примеры применения.
- •Основные понятия о науке газодинамике
4Адиабатный процесс
Адиабатный процесс – это процесс, при котором рабочее тело не обменивается теплотой с окружающей средой (dq=0). Для получения графика процесса в p-v координатах выполним некоторые преобразования.
В
соответствии с первым законом термодинамики
dq=cv·dT+p·dv=c·dT, где с – теплоёмкость
термодинамического процесса. Тогда
можно записать,
что
![]()
Продифференцируем
уравнение состояния идеального газа и
запишем:
![]()
Так
как R=cp-cv, то выражение (4.15) можно переписать
с учётом (4.16) следующим образом:

В
адиабатном процессе dq=0, то есть c·dT=0.
Поэтому c=0. Значит в адиабатном процессе
![]() .
Эту величину принято обозначать буквой
.
Эту величину принято обозначать буквой
![]() и называть показателем адиабаты.
и называть показателем адиабаты.
Поэтому в p-v координатах адиабатный процесс изображается неравнобокой гиперболой vk·p=const (рис. 4.4). Так как k>1, то адиабата проходит круче гиперболы. Адиабатный процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).
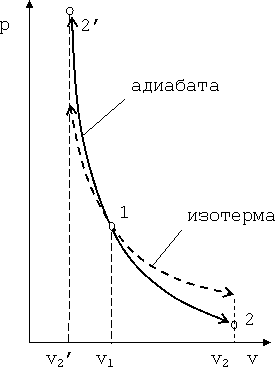
Рис. 4.4. График адиабатного процесса в p-v координатах
Запишем
для точек 1 и 2 уравнения состояния
p1·v1=R·T1; p2·v2=R·T2. Так как в адиабатном
процессе p1·v1k=p2·v2k, то
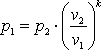 ,
,
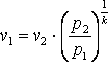 .
.
Энтропия газа в адиабатном процессе не изменяется, так как dq=0. Поэтому в T-s координатах адиабатный процесс изображается прямой линией, параллельной оси температур.
5. Политропный процесс
Политропным процессом называется любой произвольный процесс изменения состояния рабочего тела, происходящий при постоянной теплоёмкости сп.
В политропном процессе dq=cп·dT.
Для получения графика политропного процесса в p-v координатах будем придерживаться тех же рассуждений, что и при получении графика адиабатного процесса. Заменим в соотношениях, полученных при изучении адиабатного процесса, обозначение теплоёмкости с на сп и обнаружим, что p·vn=const, а . В дальнейшем всё, что написано об адиабатном процессе, можно распространить на описание политропного процесса, заменяя в выражениях k на n.
Покажем, что адиабатный процесс делит все процессы на две группы: на процессы, в которых теплоёмкость больше нуля, и на процессы, в которых теплоёмкость меньше нуля.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Из последнего выражения видно, что при n>k cп>0, а при k>n>1 cп<0.
В заключение отметим, что все рассмотренные ранее процессы – это частные случаи политропного процесса.
При n=k имеем адиабатный процесс. При n=0 имеем р1·v10=р2·v20, то есть изобарный процесс (p1=p2).
При n=1 имеем р1·v1= р2·v2, то есть изотермический процесс.
Вопрос 13
12. Первая теорема подобия. Преобразование дифференциального уравнения в критериальное. Подобие начальных и граничных условий
Для начальных и граничных условий должно соблюдаться геометрическое, временное и физическое подобие, как и для других сходственных точек натуры и модели.
Константы подобия Kl, K, K и т.д., выражающие отношение различных одноимённых величин в натуре и в модели, постоянны для различных сходственных точек подобных систем, но изменяются в зависимости от соотношения натуры и модели.
Важное свойство констант подобия: входящие в них одноименные величины могут взаимно заменяться. Поэтому отношение приращений этих величин можно заменять отношениями величин.
Например, справедливо следующее:
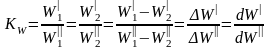 .
(2.69)
.
(2.69)
Подобие потоков в натуре можно охарактеризовать также с помощью инвариантов подобия, выражая все подобные величины в относительных единицах, т.е. в виде отношений сходственных величин в пределах каждой системы. Из уравнения (2.64) следует
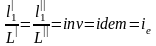 ,
(2.70)
,
(2.70)
где inv или idem - означает инвариантно или "одно и то же".
Величина ie представляет собой инвариант подобия геометрических величин.
При выражении любой величины с помощью инвариантов подобия в качестве масштаба ее измерения может быть выбрано значение этой величины в любой точке системы.
Например, в выражении (2.70) за масштаб вместо длин труб L| L|| можно принять их диаметры и т.д.
Аналогично следует:
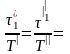 iτ
,
iτ
, 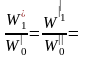 iw,
iw, 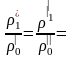 iρ,
iρ, 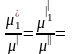 iμ.
iμ.
Инварианты подобия не зависят от размеров натуры и модели. Это означает, что при переходе oт одной системы к другой, ей подобной, инварианты подобия не меняют своих значений.
Инварианты подобия двух однородных физических величин (параметров) называются параметрическими критериями, или симплексами.
Инварианты подобия могут быть выражены также отношениями разнородных величин, т.е. представлять собой безразмерные комплексы этих величин.
Например:
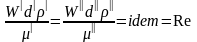 .
(2.71)
.
(2.71)
Инварианты подобия, выраженные комплексами величин, полученными преобразованиями дифференциальных уравнений, описывающих процесс, называются критериями подобия или обобщенными переменными.
Основные положения подобия обобщаются теоремами подобия.
Как получают критерии подобия? Проследим последовательность такой операции на примере подобного преобразования второго закона Ньютона.
1. Дифференциальное уравнение, описывающее данный класс явлений:
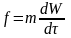 .
(2.72)
.
(2.72)
Формулируется подобие условий однозначности для группы подобных явлений, т.е. задают константы подобия: Kf, Km, KW, K..
2.
Каждую величину, входящую в дифференциальное
уравнение, умножают на
соответствующую
константу
подобия и выносят
константы как постоянные величины за
знак дифференциала: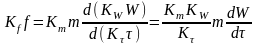 .
(2.73)
.
(2.73)
Если в уравнение входят производные более высоких порядков, то для любой физической величины (U) можно записать:
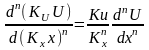 .
(2.74)
.
(2.74)
3.
Исходные и преобразованные таким образом
уравнения могут быть тождественны
лишь при условии, что индикаторы подобия
равны единице.
В
данном
случае это условие имеет вид: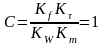 . (2.75)
. (2.75)
4.Заменяют масштабные множители в индикаторе подобия отношениями соответствующих величин и находят критерии подобия, т.е.
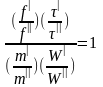 или
или
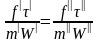 ;
откуда
;
откуда 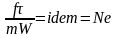 .
(2.76)
.
(2.76)
Этот подход возможен для преобразования любых дифференциальных уравнений.
Более
простой способ преобразования состоит
в следующем: делят одну часть уравнения
на другую и отбрасывают знаки математических
операторов. Полученный критерий
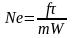 можно рассматривать как частное от
деления f
на m(dW/d)
после отбрасывания знаков дифференциала,
т.е. учитывая, что dW/dW/.
можно рассматривать как частное от
деления f
на m(dW/d)
после отбрасывания знаков дифференциала,
т.е. учитывая, что dW/dW/.
Первая теорема подобия (была сформулирована Ньютоном):
Подобные системы характеризуются численно равными критериями подобия. Первая теорема указывает, какие величины следует измерять при проведении опытов, результаты которых надо обобщать: надо измерять те величины, которые входят в критерии подобия.
