КИНЕМАТИ

Минимальный курс физики.

Составлен доц. Юнусовым Н.Б.

ОГЛАВЛЕНИЕ. Стр.

Физика, ч.1. 2

(Физические основы механики. Механические колебания и волны.

Молекулярная физика и термодинамика).

1. Основы кинематики. 2

2. Основы динамики. 4

3. Законы сохранения в механике. 6

4. Механика твердого тела. 8

5. Релятивистская динамика. 11

6. Механические колебания. 13

7. Механические волны. 15

8. Основы молекулярно-кинетической теории. 17

9. Функции распределения Максвелла и Больцмана. 20

10. Основы термодинамики. 21

Физика, ч.2. 29

(Электростатика. Электродинамика. Электромагнетизм.

Электромагнитные колебания и волны).

2.1. Электрическое поле в вакууме. 29

2.2. Электрическое поле в веществе. 33

2.3. Электрический ток. 37

2.4. Магнитное поле в вакууме. 41

2.5. Магнитное поле в веществе. 48

2.6. Основы теории электромагнитного поля. 52

2.7. Электромагнитные колебания. 54

2.8. Электромагнитные волны. 56

Физика, ч.3. 58

(Волновая и квантовая оптика. Основы квантовой механики.

Физика атома и твердого тела. Физика ядра и элементарных частиц).

3.1. Интерференция и дифракция света. 58

3.2. Поляризация и дисперсия света. 62

3.3. Тепловое излучение. 66

3.4. Фотоэффект. Эффект Комптона. Давление света. 68

3.5. Основные положения квантовой механики. 69

3.6. Квантовая теория атома. 74

3.7. Элементы физики твердого тела. 80

3.8. Ядро атома. 81

3.9. Элементарные частицы. 85

ФИЗИКА. Часть 1.

1. Основы кинематики.

Кинематика поступательного движения.

Простейшая форма движения материи – механическое движение, т.е. изменение положения материальных тел в пространстве и во времени. Кинематика изучает движение тел без рассмотрения причин, его вызывающих. Простейшей физической моделью тела является материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь. Для описания движения материальной точки необходима система отсчета: часы для отсчета времени и система ко­ординат (обычно выбирают прямоугольную декартову систему координат). Положение материальной точки в момент времени t опреде­ляется координатами х, у, z или радиус-вектором . Модуль и направление радиус-вектора опреде­ляются тремя его проекциями на оси координат: , , где , , – единичные векторы направлений (орты). В процессе своего движения точка описыва­ет некоторую линию, называемую траекторией. Расстояние, пройденное материальной точкой по траектории, представляет собой путь s. Век­тор , соединяющий начальную и конечную точ­ки траектории, называется перемеще­нием. Зависимости координат материальной частицы x = x(t), y = y(t), z = z(t) или ее радиус-вектора от времени называются кине­матическими уравнениями движения.

Мгновенная скорость материальной точ­ки в момент времени t есть первая производная по времени от радиус-вектора движущейся материальной точки:

.

Вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке. Проекции вектора скорости на координатные оси х, у и z равны , , , а вектор и модуль скорости определяются выражени­ями: и .

Характеристикой изменения скорости является ускорение . В общем случае произвольного дви­жения ускорение материальной точки в данный момент времени определяется как первая произ­водная от вектора скорости (или вторая производная от радиус-вектора) по времени: .

В каждой точке траектории вектор ускорения можно разложить на две составляющие: одна из них направлена по касательной к траектории в данной точке и называется тангенциальным ускорением , другая – по нормали к траек­тории и называется нормальным, или цент­ростремительным, ускорением . Танген­циальное ускорение определяет изменение величины вектора скорости, а центростреми­тельное ускорение – изменение его направле­ния в данной точке траектории. Тангенциальное и нормальное ускорения определяются выраже­ниями: ; . R – радиус кривизны. Полное ускорение равно , так как .

Путь, пройденный за промежуток времени от момента t₁ до t₂,:

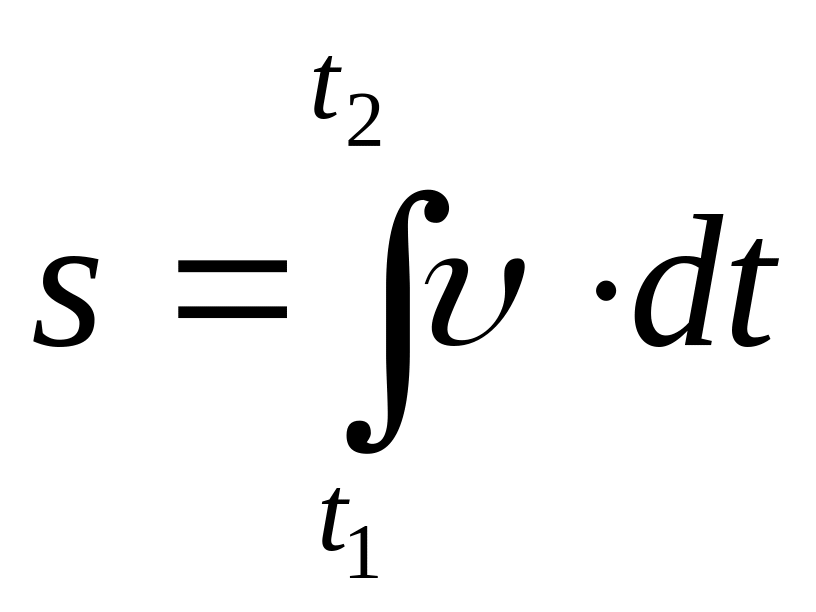, где υ – модуль скорости.

Кинематика вращательного движения.

Если точка вращается вокруг неподвижной оси , то она описывает окружность с центром на оси вращения, а плоскость этой окружности перпендикулярна оси вращения. Быстроту и направление вращения характеризуют угловой скоростью , равной первой производной от углового перемещения по времени: .

В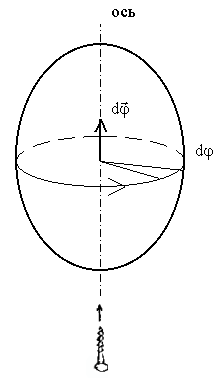 ектор угловой скорости (так же как и угловое перемещение d ) перпендикулярен плоскости окружности, по ко­торой движется точка, направлен по оси вращения и связан с направлением вращения правилом правого винта. Тогда векторы угловой и линей­ной скоростей связаны соотношением: , где –радиус-вектор движущейся точки, а квадратные скобки означают векторное про­изведение. Модуль вектора линейной скорости υ=ω· r_A , где r_A – радиус окружности, по которой дви­жется эта точка.

Для характеристики неравномерного движе­ния по окружности используется векторная ве­личина, называемая угловым ускорением и определяемая соотношением:

.

Если движение материальной точки ускорен­ное, то векторы угловой скорости и углового ускорения совпадают по направлению; если дви­жение замедленное, то эти векторы направлены в противоположные стороны. Такие векторы, на­правление которых совпадает с направлением некоторой оси, называются аксиальными. У них нет определенной точки приложения, они могут изображаться в любом месте на оси вращения.

При равнопеременном вращении для вели­чин угловой скорости и углового ускорения вы­полняются соотношения (аналогичные соотно­шениям для линейной скорости и линейного ускорения): .