Вопрос 2

Географической картой называется уменьшенное обобщенное изображение земной поверхности на плоскости, полученное по определенному математическому закону. Картографической проекцией называется матем. закон осуществл. связь между положением точки на земной поверхности и положением изображения этой точки на карте.

Н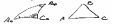 а поверхности шара сферический треугольник АоВ₀Со стороны которого образованы дугами больших кругов, т.е. кратчайшими линиями. Предположим, что шар можно развернуть на плоскость с сохранением элементов внутренней геометрии, т.е. утлы, площадь, гауссова кривизна поверхности, и свойства кратчайших линий оставаться кратчайшими. В таком случае треугольник ABC будет с прямыми линиями, а углы его будут равны углам сферического треугольника. Но сумма углов плоского треуг. А+В+С=180, а сферического А+В+С=180+сферический избыток. Изобразить шар или сфероид на плоскости можно различными способами: Сохранить углы, но тогда кратчайшие линии на сфероиде уже не будут прямыми на плоскости, а масштаб не будет постоянным. Сохранить постоянство масштаба площадей, но тогда исказятся углы и кратчайшие линии не будут прямыми на плоскости. Сохранить кратчайшие линии кратчайшими, но тогда будут искажены и углы и площади. Система координатных линий нанесенная на земной сфероид или на шар образует координатную сетку. При составлении карт координатную сетку переносят на плоскость проекции, где она образует картографическую сетку.

Классификация картографических проекций: 1.Цилиндрическими наз. Проекции, у которых параллели - параллельные между собой прямые, а меридианы - прямые перпендикулярные параллелям. Удаление параллелей от экватора является функцией широты; расстояния между меридианами пропорциональны разности долгот. У-ние цилиндрической проекции х= f(φ); у=с(λ) 2.Азимутальными назыв. Проекции у которых параллели нормальной сетки - концентрические окружности, а меридианы - радиально расходящиеся из центра окружностей прямые. Углы между меридианами сетки равны разности долгот. Ур-ния меридианов и параллелей нормальной сетки ?, азимутальных проекциях: δ =λо, ρ= f(φ); где δ - угол между меридианами нормальной сетки; λо - угол между меридианами на поверхности земли; ρ - радиус параллели нормальной сетки. 3.Коническими наз. проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели изображаются концентрическими окружностями имеющими общий центр в точке пересечения меридианов. Ур-ние: λ =α λо; ρ= f(φ); где α - коэф. пропорциональности называемый показателем конической проекции (при α =1 - азимутальная проекция явл. частным случаем конической).

Д ля использования в судовождении морская карта должна удовлетворять след требованиям.: 1. карта должна быть равноугольной, т.е. углы пеленги и курсы не должны искажаться. 2. линия пути судна, составляющая с меридианами постоянный угол, должна изображаться на проекции прямой линией (локсодромией).

Этим требованиям отвечает только равноугольная цилиндрическая проекция Меркатора.

На полусфере проведены параллели LL, MM, NN через одинаковые разности широт и меридианы РnА, РnВ, РnС, PnD через равные разности долгот. На модель земного шара наденем цилиндр, так чтобы его ось совпала с осью земли, и спроектируем градусную сетку на внутреннюю поверхность цилиндра путем выпрямления меридианов, сохраняя их длину неизменной. При этом параллели растянутся и каждая из проекции станет равной экватору: ll=mm =nn=eq. Этим соблюдается первое требование: получилась прямоугольная проекция. Однако такая проекция еще не является комфортной, т.к. параллели были растянуты и фигуры в натуре и на проекции не будут подобными Для того, чтобы проекцию комфортной, необходимо ее растянуть в меридиональном направлении на столько, чтобы в данной широте растянулась параллель при проектировании на цилиндр. Длина экватора EQ=2πR, где R - радиус земли. Длина параллели на сфере ММ=2πRм, где Rм - радиус параллели ММ. EQ/MM= 2πR /2πR cos φ= l/ cos φ =sec φ

Т.е. при проектировании на стенки цилиндра длинна каждой параллели увеличилась в sec φ раз, значит и меридианы нужно вытянуть в каждой точке в sec φ раз.