26. Числовой ряд. Сумма ряда
Определение
Пусть
—
последовательность чисел. Число
называется
n-ой
частичной суммой
ряда
.
Сумма
(числового) ряда —
это предел частичных сумм Sn,
если он существует и конечен. Таким
образом, если существует число
,
то в этом случае пишут
.
Свойства числовых рядов
Свойство 1. Если ряд
(1.1)
сходится и его сумма равна S, то ряд
(1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
,
а их суммы равны S1 и S2 соответственно, то сходятся и ряды
,
причём
сумма каждого равна соответственно
.
Сходимость
Ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел. Этот предел называется суммой сходящегося ряда.
№27.Необходимый признак сходимости ряда
Для
сходимости ряда (1) необходимо и достаточно,
чтобы для любого
существовало
число
такое,
что при
и
(n и p – натуральные числа) было выполнено неравенство
.
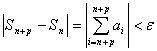В
частности, если ряд сходится, то
.
Теорема:
Если
ряд
сходится, то его общий член стремиться
к нулю, т.е.
.
Доказательство. По условию ряд
сходится.
Обозначим через S
его сумму. Рассмотрим частные суммы
ряда
и
.
Отсюда
.
Т.к.
и
при
,
то
.
Условие является необходимым, но не достаточным условием сходимости ряда.
№28. знакопостоянные ряды. сравнение рядов
Признак сравнения 1.
Теорема: Для того чтобы ряд
с неотрицательными членами сходился, необходимо и достаточно, чтобы
последовательность частичных сумм этого ряда была ограничена.
Доказательство. Необходимость. Пусть ряд
сходится. Это значит, что последовательность его частичных сумм имеет предел.
Всякая сходящая последовательность является ограниченной.
Достаточность. Пусть последовательность частичных сумм ряда
ограничена. Т.к. ряд
с неотрицательными членами, то его частичные суммы образуют не убывающую
последовательность:
. Монотонная ограниченная последовательность сходится, т.е. сходится ряд
.
Признак сравнения 2.
Теорема : Пусть даны два ряда с неотрицательными членами
и
и
для всех
n
выполняется неравенство
. Тогда из сходимости ряда
следует сходимость ряда
, а из сходимости ряда
следует сходимость ряда
.
Доказательство.
Обозначим через
и
соответственно
частичные суммы рядов
и . Из неравенства
следует, что
Если ряд сходится,
то по теореме (необходимость) последовательность его частичных сумм
ограничена,
т.е. для любого n
,
где М
– некоторое число. Но тогда по формуле
(7) и
, откуда по той же теореме 5 (достаточность) следует, что ряд
сходится.
Если же ряд
расходится, то ряд
также расходится, т.к., допустив сходимость ряда
получим по только что доказанному сходимость ряда
, а это противоречит условию теоремы.
№29. Признак Даламбера.
Теорема 7: Пусть дан ряд
с
положительными членами и существует
предел
.
Тогда
а) при
ряд сходится;
b)
при
ряд расходится.
Доказательство.
a) Пусть
и . Докажем, что ряд
сходится. По определению предела числовой последовательности для любого
существует
номер N
такой, что при
выполняется
неравенство
.
Отсюда следует, что
(8)
Т.к.
,
то
можно
взять настолько малым, что будет выполнено
неравенство
.
Полагая
,
на
основании
правого из неравенств (8) имеем
,
или
для n=N,
N+1, N+2, . Придавая n эти значения, из последнего неравенства
получаем
т.е.
члены ряда
(9)
меньше соответствующих членов ряда, составленного из элементов геометрической
прогрессии:
(10)
Т.к.
,
то ряд (10)
сходится. Тогда согласно признаку сравнения ряд (9) также сходится. Но ряд (9)
получен из данного ряда
в результате отбрасывания конечного числа первых членов, следовательно, по
теореме 1 ряд
сходится.
b) Пусть теперь .
Докажем, что ряд
расходится. Возьмем
настолько
малым, чтобы
. Тогда при в силу
левого
из неравенств (8) выполняется неравенство
или
.
Таким образом,
члены ряда, начиная с некоторого номера N, возрастают с увеличением их
номеров,
т.е. общий член ряда
не стремится к нулю при
. Следовательно, согласно теореме 4, ряд
расходится.
Замечание.
При
ряд
может, как сходится, так и расходится. В этом случае необходимо дополнительное
исследование ряда с помощью признака сравнения или других признаков.