22.Определитель Вронского.Структура решения неоднор ду

Определителем Вронского W(x; y₁(x), y₂(x), ..., y_n(x)) называется определитель, первая строка которого образована функциями y₁(x), y₂(x), ..., y_n(x) из C_n-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:

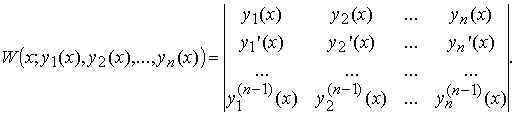
Справедливо следующее необходимое условие линейной зависимости функций.

Если функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно равен нулю на этом отрезке: W(x; y₁(x), y₂(x), ..., y_n(x)) ≡ 0 на[a;b].

Важно понимать, что обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Однако, если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке.

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения:

.

23.Лин однор ду с пост коэф

обыкновенное дифференциальное уравнение вида:

где

- y = y(t) — искомая функция,

- y^(k) = y^(k)(t) — её k-тая производная,

-  — фиксированные числа,

- f(t) — заданая функция (когда , имеем линейное однородное уравнение, иначе — линейное неоднородное уравнение).

24.Линейные неоднор ду.Метод Лагранжа

Метод вариации постоянных

Если общее решение y₀ ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.  Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C₁ и C₂ будем рассматривать вспомогательные функции C₁(x) и C₂(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x).  Неизвестные функции C₁(x) и C₂(x) определяются из системы двух уравнений:

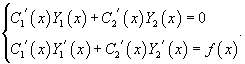
25.Лин неоднорДу с пост коэф

т.е. уравнения вида , записывается в виде , где - общее решение соответствующего однородного уравнения, а - какое-либо частное решение неоднородного уравнения.

Укажем способ, позволяющий найти частное решение неоднородного уравнения по виду правой части. Заметим, что это возможно лишь в случаях, когда правая часть уравнения является функцией определенного вида.

1.                   Пусть , где - некоторое число, не равное нулю. Тогда

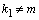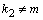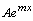• если, , , то частное решение уравнения ищут в виде , где 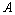- неизвестное число, которое находят, подставляя 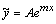 в неоднородное уравнение

 если , а , то в этом случае частное решение ищут в виде ;

 наконец, если и  и , т.е. , то .

2. Если           , где  – многочлен степени , то

 при ,  решение ищут, просто «передразнивая» правую часть, т.е. , как и правая часть, должна представлять собой произведение многочлена той же степени, что и в правой части уравнения, но с неопределенными коэффициентами, и ,т.е. . В частности, если , то ;

при ,  частное решение  ищут в виде ;

 при  находим  по формуле .