- •Вопрос 1. Метод Монжа. Эпюры точек, расположенных в четвертях и отантах пространства.
- •Вопрос 2 Проекции отрезка прямой.Положение прямой относительно плоскойстей проекций.
- •Вопрос 3. Деление отрезка прямой в заданом отношении
- •Вопрос 5. Следы прямой
- •Вопрос 6. Принадлежность точки прямой.
- •Вопрос 7. Проецирование прямого угла
- •Вопрос 8. Взаимное положение прямых. Конкурирующие точки
- •Вопрос 9. Способы задания плоскости на эпюре
- •Вопрос 10 . Следы плоскости
- •Вопрос 11. Положение плоскости относительно плоскостей проекций
- •Вопрос 12. Принадлежность прямой и точки плоскости.
- •Вопрос 13. Главные линии плоскости. Линии наибольшего наклона. Построение углов наклона плоскости к плоскостям проекций.
- •Вопрос 14. Проведение проецирующей плоскости через прямую.
- •Вопрос 15. Прямая, параллельная плоскости.
- •Вопрос 16. Параллельные плоскости
Вопрос 1. Метод Монжа. Эпюры точек, расположенных в четвертях и отантах пространства.
Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала 19 веков, 1789-1818 гг. одним из основателей знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов.
Постепенно накопившиеся отдельные правила и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometrie descriptive".
Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления техническихчертежей.
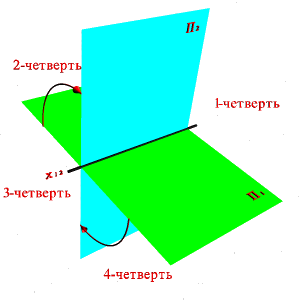
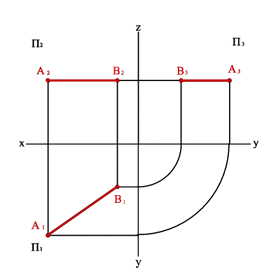
В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. П1 - горизонтальная плоскость проекций, П2- фронтальная. Плоскости бесконечны и непрозрачны.
Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.
|
|
Линия пересечения плоскостей проекций называется осью координат и обозначается x12. Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти. Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2(рис.6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа (франц. Epure – чертеж.) ил комплексным чертежом. Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные(многогранники, одномерные и двумерные обводы). Рассмотрим способы их образования, графического задания и возможные варианты положения по отношению к плоскостям проекций. |
|
|
Вопрос 2 Проекции отрезка прямой.Положение прямой относительно плоскойстей проекций.
Проекции отрезка прямой - ОТСКАНИТЬ стр. 20 умк 1
Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
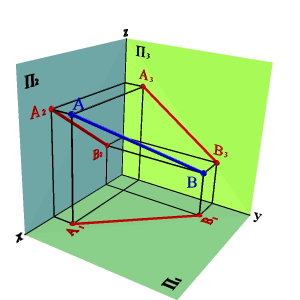
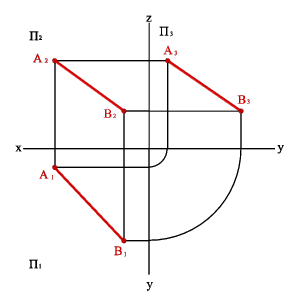
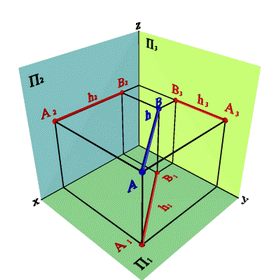
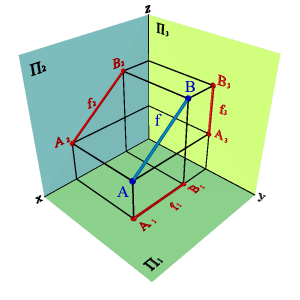
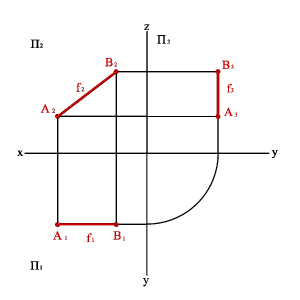
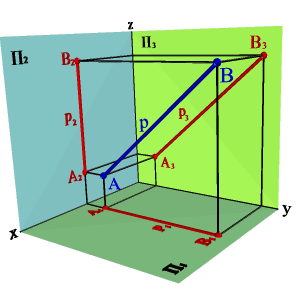
Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.18).
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 18. Прямая общего положения |
|||
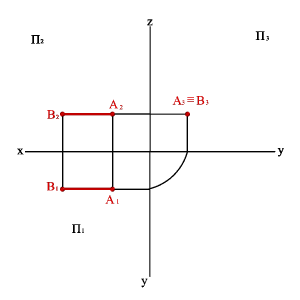
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.19). Для любой пары точек горизонтали должно быть справедливо равенство
zA=zB A2B2//0x; A3B3//0y xA–xB≠0, yA–yB≠0, zA–zB=0.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 19. Горизонтальная прямая |
|||
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями (рис.20).
yA=yB A1B1//0x, A3B3//0z xA–xB≠0, yA–yB=0, zA–zB≠0.
|
|
|
|
|
|
||||
|
||||
а) модель |
б) эпюр |
|||
Рисунок 20. Фронтальная прямая |
||||
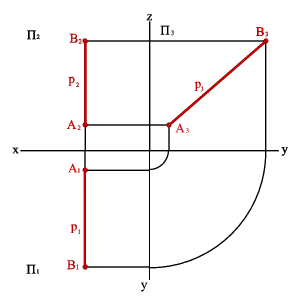
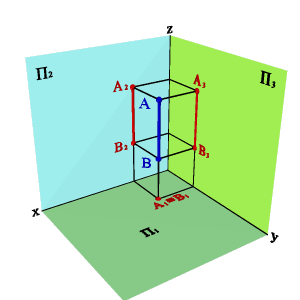
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 21).
xA=xB A1B1//0y, A2B2//0z xA–xB=0, yA–yB≠0, zA–zB≠0.
Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 21. Профильная прямая |
|||
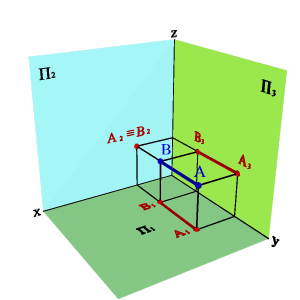
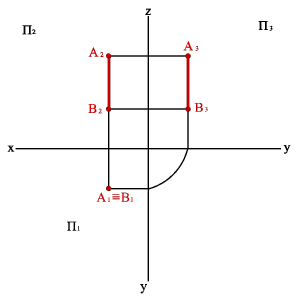
3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально проецирующая прямая - АВ (рис. 22)
xA–xB=0
yA–yB≠0
zA–zB=0,
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 22. Фронтально проецирующая прямая |
|||
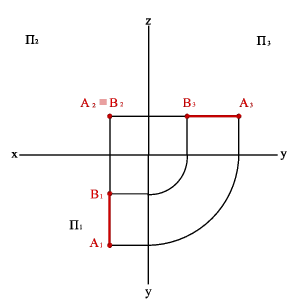
3.2. Профильно проецирующая прямая - АВ (рис.23)
xА–xB≠0
yА–yB=0
zА–zB=0,
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 23. Профильно-проецирующая прямая |
|||
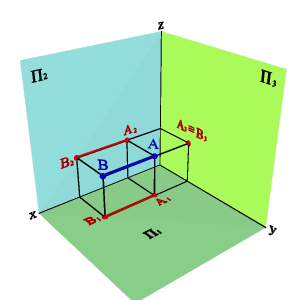
3.3. Горизонтально проецирующая прямая - АВ (рис.24)
xА–xВ=0
yА–yВ=0
zА–zВ≠0.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 24. Горизонтально-проецирующая прямая |
|||
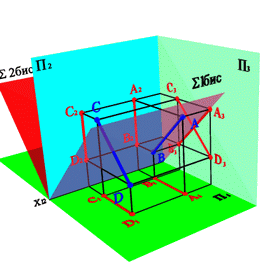
4. Прямые параллельные биссекторным плоскостям (рис. 25)
АВ 1бис xA–xB=0; zB–zA=yB–yA;
СD//2бис xС–xD=0; zD–zC=yC–yD.
Биссекторной плоскостью называется плоскость, проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П1 и П2 пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (1бис), а через 2 и 4 четверти - второй (2бис).
5. Прямые перпендикулярные биссекторным плоскостям (рис. 25)
АВ2бис xA–xB=0; zB–zA=yВ–yА;
СD1бис xС–xD=0; zD–zC=yC–yD.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 25. Прямые параллельные и перпендикулярные биссекторным плоскостям
|
|||