36.Теоремы о дифференцировании

Рассматриваются действительнозначные функции на отрезке действительной оси.

Теорема о дифференцировании под пределом

функция непрерывно дифференцируема на отрезке

сходится

на отрезке

Тогда  — непрерывно дифференцируема на , на

Теорема о почленном дифференцировании.

функция непрерывно дифференцируема на отрезке

сходится

равномерно сходится на отрезке

Тогда 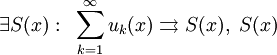 — непрерывно дифференцируема на ,

на

№37. Степенные ряды. Интервал сходимости

Степенные ряды

Среди функциональных рядов особое место занимают степенные ряды,

которые выделяются своей прикладной значимостью.

Определение: Функциональный ряд вида

а 0 + а1 x + а 2 x + а 3 x + ... + а n x + ... = ∑ аn x n ,

n =0

где а1 , а 2 , ..., а n , ... – числовые коэффициенты, называется степенным рядом

по степеням х.

Рассматривают также ряд вида

∞

а 0 + а1 ( x − a ) + а 2 ( x − a ) 2 + ... + а n ( x − a) n + ... = ∑ а n ( x − a) n ,

n=0

где а, а 0 , а1 , а 2 , ..., а n , ... – постоянные. Этот ряд называется степенными

рядом по степеням (х – а).

Заметим, что ряд по степеням х сходится в точке х=0 и его сумма в этой

точке равна нулю. О существовании других точек сходимости, если они

существуют, говорит теорема Абеля.

∞

Теорема Абеля. Если степенной ряд ∑ аn x n :

n =0

1) сходится при х = х 0 ≠ 0 , то он сходится при всех х, удовлетворяющих

неравенству х < x0 ;

2) расходится при х = х0, то он расходится при всех х, удовлетворяющих

неравенству х > x0 .

Из теоремы Абеля следует, что если степенной ряд сходится в одной

точке x 0 ≠ 0 , то он сходится во всех точках, принадлежащих интервалу

− х0 < x < x0 .

Рассмотрим степенной ряд ∑ an x n .

n =0

Определение: Число R > 0 называется радиусом сходимости степенного

∞

ряда ∑ an x n , а интервал (– R; R) – интервалом сходимости этого ряда, если

n =0

∀x : х < R данный ряд сходится, а ∀x : x > R этот ряд расходится.

∞

Если степенной ряд ∑ a n x n сходится только при х = 0, то полагают R = 0,

n =0

если же этот ряд сходится ∀х ∈ (− ∞; ∞ ) , то считают R = ∞ .

Отметим следующее: Если R>0 – радиус сходимости ряда ∑ а n x n , то

n =0

∞

∀x ∈ (− R; R ) ряд ∑ an x n – сходится и имеет сумму S(x), т.е.

n =0

∞

∀x ∈ (− R; R ) ∑ a n x n = S ( x ) .

n =0

Найдем формулы для вычисления радиуса сходимости ряда

∞

∑ an x n .

n =0

a n +1

Предположим, что существует конечный или бесконечный lim = λ.

n→∞ a n

a n +1 x n +1

Найдем для данного ряда те значения х, для которых lim < 1 , т.е.

n →∞ an x n

a n +1

воспользуемся признаком Даламбера. Получим х ⋅ lim < 1. Это

n →∞ a n

неравенство будет выполняться для ∀х : х <1. Очевидно, что для ∀x,

an

lim a +1

n →∞ n

удовлетворяющих неравенству х > 1 степенной ряд будет расходиться.

аn +1

lim

n → ∞ аn

Значит, из определения радиуса сходимости степенного ряда следует, что

аn

R= 1 = lim .

аn +1 n →∞ а n +1

lim

n → ∞ аn

Радиус сходимости степенного ряда можно находить и с помощью

радикального признака Коши.

Предположим, что существует lim n а n ≠ 0 . Найдем, для каких х

n →∞

выполняется условие:

lim n аn x n < 1 ⇒ x lim n аn < 1 ⇒ 1 x .

n →∞ n →∞ lim n аn

n →∞

Очевидно, что ∀х : х > 1 , степенной ряд расходится. Следовательно,

lim n аn

n →∞

получаем: R = lim 1 .

n →∞ n аn

Мы установили, что ∀х : х < R степенной ряд сходится, а ∀х : х > R

этот ряд расходится. Не исследованными остаются только две точки x = ± R .

Изучив поведение ряда в этих двух точках, мы будем знать множество всех

точек сходимости, т.е. область сходимости степенного ряда.