
- •1.Таблица производных
- •Элементарные функции
- •2.Таблица интегралов
- •3.Тройной интеграл его вычисление
- •4. Замена переменной в тройном интеграле
- •7. Криволинейный интеграл 1го рода и его вычисление
- •8.Криволинейный интеграл 2го рода и его выч
- •9.Вычисление площади области ограниченной прямой
- •10.Касательная плоскости и нормаль к поверхности
- •11. Поверхн. Интеграл 1го рода
- •12.Поверхностный интеграл 2го рода и его выч
- •13.Д,у. Осн понятия. Задача Коши
- •14.Ду с разделяющимися переменными
- •15.Однородные уравнения
- •16.Линейные ду 1го порядка.Метод подстановки Бернули
- •Метод Бернулли
- •17 Метод вариации произвольного постоянного
- •18.Уравнение Бернули
- •19.Ду в полных дифференциалах
- •20.Ду высших порядков. Задача Коши
- •21.Ду допускающее понижение порядков
- •22.Определитель Вронского.Структура решения неоднор ду
- •23.Лин однор ду с пост коэф
- •24.Линейные неоднор ду.Метод Лагранжа
- •25.Лин неоднорДу с пост коэф
- •26. Числовой ряд. Сумма ряда
- •30.Радикальный признак коши
- •33. Знакопеременные
- •36.Теоремы о дифференцировании
- •38.Формулы для вычисления радиуса сходимости степенного ряда. Свойства степенных рядов.
- •40. Разложения в ряд Маклорена ех
- •41. Разложения в ряд Маклорена некоторых функций
- •42. Разложения в ряд Маклорена некоторых функций
- •43.Примерение рядов для постр решений ду
- •44.Прим рядов для вычисл определ интеграла
- •46.Тригонометрический ряд Фурье
- •47. Разложение в ряд Фурье 2l – периодичных функций
- •48. Ряд Фурье для четных и нечетных функций
- •49. Разложение в ряд Фурье непериодических функций
- •50. Комплексная форма ряда Фурье
- •51. Преобразование Фурье
- •52. Ряд Фурье по полной замкнутой системе ортогональной функции
- •53. Понятие о функции комплексной переменной
- •54. Дифференцируема функция комплексного переменного
19.Ду в полных дифференциалах
Дифференциальное уравнение вида
![]()
называется
дифференциальным
уравнением в полных диффернциалах,
если его левая часть является полным
дифференциалом
некоторой гладкой функции
![]() ,
т.е. если
,
т.е. если
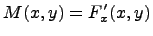 ,
,
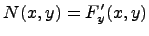 .
Необходимое и достаточное условие для
существования такой функции имеет вид:
.
Необходимое и достаточное условие для
существования такой функции имеет вид:
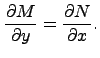
Чтобы
решить дифференциальное
уравнение в полных дифференциалах
необходимо найти функцию
.
Тогда общее решение дифференциального
уравнения
можно записать в виде
![]() для
произвольной постоянной
для
произвольной постоянной
![]() .
.
20.Ду высших порядков. Задача Коши
Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида F(x, y, y', y'', ..., y(n)) = 0,
Функция y(x) называется решением дифференциального уравнения n-го порядка, если она n раз непрерывно дифференцируема на промежутке (a, b) и удовлетворяет уравнению для всех xО(a, b).
Дифференциальное уравнение n-го порядка имеет, вообще говоря, бесконечное множество решений. Чтобы выделить единственное решение уравнения достаточно определить начальные условия: y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1.
При определенных ограничениях на правую часть уравнения эта задача, она называется задачей Коши, имеет единственное решение.
Справедлива следующая теорема существования и единственности решения задачи Коши. Если правая часть уравнения y(n)) = f(x, y, y', y'', ..., y(n-1)) и ее частные производные по переменным y, y', y'', ..., y(n-1) непрерывны в области GМ Rn+1, то для любой точки (x0, y0, y0,1, y0,2, ..., y0,n-1) из G на некотором интервале (x0-h, x0+h) существует единственное решение y(x) уравнения, удовлетворяющее начальным условиям y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1.
Численное решение задачи Коши y(n)) = f(x, y, y', y'', ..., y(n-1)), y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1 состоит в построении таблицы приближенных значений yi решения y=y(x) в точках x1, x2, ..., xi, ... .
Задача о численном решении дифференциального уравнения порядка выше первого чаще всего сводится к численному решению задачи Коши для нормальной системы дифференциальных уравнений. Обозначив y(x)=y1(x), y'(x)=y2(x), y''(x)=y3(x), ..., y(n-1)(x)=yn (x), получим задачу Коши для системы n дифференциальных уравнений 1-го порядка y1'=y2 , y2'=y3 , ..., yn' =f(x, y1, y2 , ..., yn ), y1(x0 )=y0, y2(x0)=y1,0 , ..., yn-1(x0)=yn-1,0, которая в векторной форме имеет вид `Y '= `F(x,`Y), `Y(x0) =`Y0, `Y (x)=(y1(x), y2(x), ..., yn(x)), `Y '(x)=(y1'(x), y2'(x), ..., yn'(x)), `F(x,`Y)= (y2, y3, ..., yn, f(x, y1, y2 , ..., yn )).
21.Ду допускающее понижение порядков
Уравнение, не содержащее явно независимой переменной
![]()
![]()
![]()
![]()
Подстановка y' = p понижает порядок уравнения на единицу.
При
этом 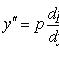
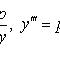
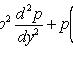
![]() и
т. д.
Уравнение,
не содержащее искомой функции
и
т. д.
Уравнение,
не содержащее искомой функции
![]()
![]()
![]()
![]()
Подстановка y' = p понижает порядок на единицу.
В общем случае
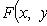
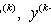
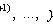
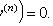
Подстановка 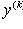
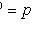 понижает
порядок на k единиц.
понижает
порядок на k единиц.
Уравнение, однородное относительно переменных y, y', ..., y(n)
![]()
![]()
![]()
![]()
где ![]()
![]()
![]()
![]()
![]() .
.
Подстановка z = y'/y понижает порядок уравнения на единицу.
Обобщенное однородное уравнение \
где ![]()
![]()
![]()
![]()
![]() .
.
Вводя
новые переменные t и z по
формулам ![]()
![]()
![]()
![]() ,
приходим к уравнению, не содержащему
явно t и,
следовательно, допускающему понижение
порядка.
,
приходим к уравнению, не содержащему
явно t и,
следовательно, допускающему понижение
порядка.
