52. Ряд Фурье по полной замкнутой системе ортогональной функции

Функции j(х) и y(х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если

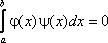
Последовательность функций j1(x), j2(x), …, jn(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.

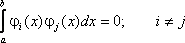
Отметим, что ортогональность функций не подразумевает перпендикулярности графиков этих функций.

Определение. Система функций называется ортогональной и нормированной (ортонормированной), если

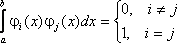
Определение. Рядом Фурье по ортогональной системе функций j1(x), j2(x), …,jn(x) называется ряд вида:

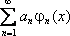
коэффициенты которого определяются по формуле:

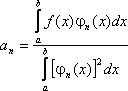
где f(x) = - сумма равномерно сходящегося на отрезке [a, b] ряда по ортогональной системе функций. f(x) – любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a, b].

53. Понятие о функции комплексной переменной

Пусть даны два множества D и Е, элементами которых являются комплексные числа

Z=x+iy (Z прин. D)

W=U+iV (W прин. E)

И будем изображать точками на плоскости:

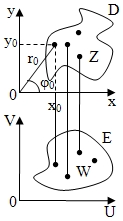
Если каждому числу (точке) Z прин. D по некоторому правилу поставлено в соответствие число (точка) W прин. Е, то говорят, что на множестве определена однозначная функция комплексного переменного W=f(z), отображающая множество D в множестве E.

Например, Z=2+3i; W=Z^2 -> W=(2+3i)^2

Если каждому Z прин. D соответствует много значений W, то функция W=f(Z) называется многозначной. Множество D называется областью определения функции W=f(Z). Множество E всех значений W=f(z) называется областью значений этой функции. Будем рассматривать множества D и E как области. Областью комплексной плоскости называется множество точек плоскости, обладающих свойствами открытости и связности.

W=U+iV=f(x+iy)=U(x;y)+iV(x;y)

Функция u(x;y) называется действительной функций комплексного переменного. Функция V(x;y) называется мнимой. Таким образом задание функции комплексного переменного равносильно заданию двух функций с действительной и мнимой частью.

Тригонометрическая:

Показательная:

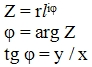
54. Дифференцируема функция комплексного переменного

Сейчас мы сформулируем и докажем важнейшую в теории ФКП теорему о необходимых и достаточных условиях дифференцируемости (а, следовательно, аналитичности) функции.

Для того, чтобы функция w = f(z) = u(x, y) + i v(x, y) была дифференцируема в точке z = x + iy, необходимо и достаточно, чтобы функции u(x, y) = Re f(z) и v(x, y) = Im f(z) были дифференцируемы в точке (х,у), и чтобы в этой точке выполнялись соотношения

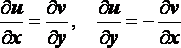
Доказательство. Необходимость. Здесь мы применим идею, которой воспользовались, когда доказывали, что функция f(z) = | z |2 = x2 + y2 не имеет производных в точках : подойдём к точке z двумя путями - по направлениям ( ) и (

В первом случае:

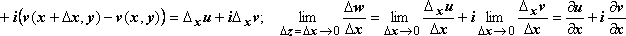
Во втором случае:

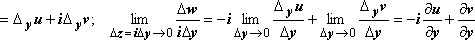
Пределы должны быть равны, поэтому .

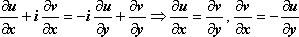
Достаточность. По предположению теоремы, функции u(x, y), v(x, y) дифференцируемы в точке (х,у), поэтому где ,

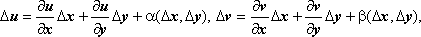
- бесконечно малые более высокого порядка по сравнению с , т.е. , . Найдём . .

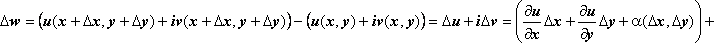
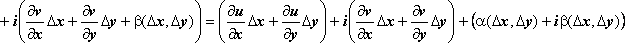
Последнее слагаемое - бесконечно малая высшего порядка по сравнению с : 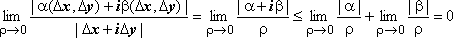; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим тогда . Отсюда следует, что существует , т.е. функция дифференцируема в точке (х,у).

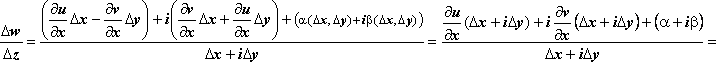
Производная дифференцируемой функции может находиться по любой из формул 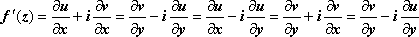, эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа: 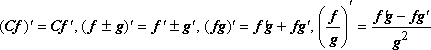(в точках, где . Элементарные функции комплексного переменного являются аналитическими во всех точках области определения, а следовательно имеют производные в каждой точке области определения, причем производные элементарных функций комплексного переменного можно вычислить, используя таблицу производных и правила дифференцирования соответствующих функций действительного переменного.