50. Множинний коефіцієнт кореляції:

Він характеризує тісноту зв’язку усіх незалежних змінних із залежною.Для множинного коефіцієнта кореляції з урахуваннням і без урахуванння числа ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації

51. Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної ( ) визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Використаємо середні квадратів відхилень (дисперсії) (див. табл. 5.2) і запишемо формулу для обчислення коефіцієнта детермінації:

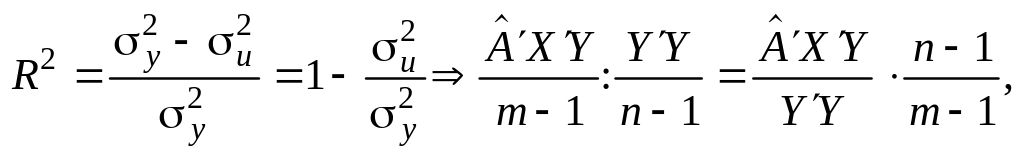або, не враховуючи ступенів свободи:

Оскільки у (5.7) задані незміщені оцінки дисперсії з урахуванням числа ступенів свободи, то коефіцієнт детермінації може зменшуватись при введені в модель нових незалежних змінних. Тоді як для коефіцієнта детермінації, обчисленого без урахування поправки (n – 1/m – 1) на число ступенів свободи (5.8), коефіцієнт детермінації ніколи не зменшується. Залежність між цими двома коефіцієнтами можна подати так:

де — коефіцієнт детермінації з урахуванням числа ступенів свободи;

— коефіцієнт детермінації без урахування числа ступенів свободи.

52. змінними можна перевірити з допомогою F-критерію: 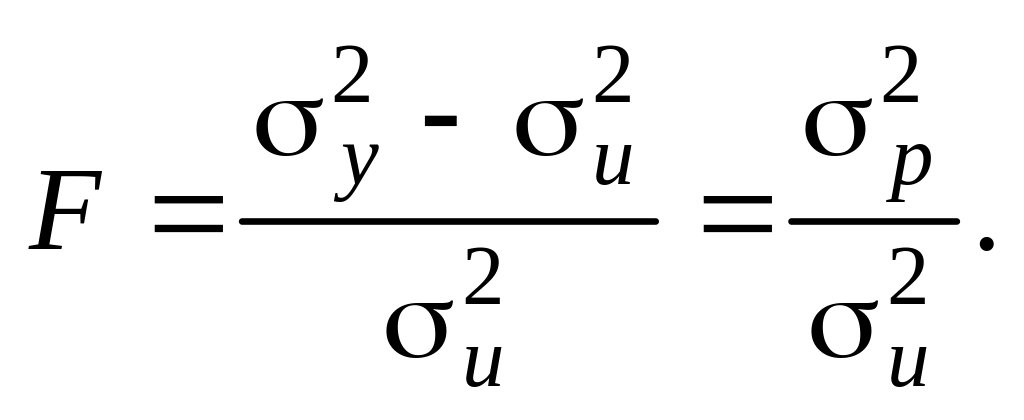(5.15)

При цьому ми виходимо з того, що залишки u розподілені нормально, тобто користуємося фундаментальною теоремою про те, що для нормально розподіленої випадкової величини з нульовою середньою і одиничною дисперсією сума квадратів її n випадково вибраних значень має розподіл з n ступенями свободи.

Дисперсії, які застосовуються для обчислення F-критерію, наведено в табл.5.2.

Фактичне значення F-критерію порівнюється з табличним при ступенях свободи n – m і m – 1 і вибраному рівні значущості. Якщо Fфакт > Fтабл, то гіпотеза про істотність зв’язку між залежною і незалежними змінними економетричної моделі підтвержується, у противному разі - відкидається.

53. Оскільки коефіцієнт кореляції є також вибірковою характеристикою, яка може відхилятись від свого “істинного” значення, значущість коефіцієнта кореляції також потребує перевірки. Базується вона на t-критерії

де — коефіцієнт детермінації моделі; — коефіцієнт кореляції; — число ступенів свободи.

Якщо , де — відповідне табличне значення t-роз­поділу з ступенями свободи, то можна зробити висновок про значущість коефіцієнта кореляції між залежною і незалежними змінними моделі.

54. На основі t-критерію і стандартної помилки побудуємо довірчі інтервали для параметрів :

55. Прогнозування на основі моделі є третім етапом економетричного моделювання звязку між еконмічнми показниками.

Розглянемо спочатку точковий прогноз і припустимо, що ми визначили його як деяку лінійну функцію від , тобто

де і — номер спостереження ( ); — вагові коефіцієнти значень . (Їх потрібно вибрати так, щоб зробити найкращим лінійним незміщеним прогнозом).

Оскільки то незміщена оцінка прогнозу

, де - матриця очікуваних значень пояснювальних змінних. Задаючи підставимо значення цього вектора в побудовану економетричну модель ,

Для визначення інтервального прогнозу індивідуального значення необхідно знайти відповідну стандартну похибку .

.Отже, інтервальний прогноз індивідуального значення визначається як

або

56. Коефіцієнти детермінації і кореляції свідчать про значущість зв’язку, який описується моделлю. показує, що на 93% варіація продуктивності праці визначається варіацією затрат на прикладні дослідження та фондомісткістю продукції. Коефіцієнт кореляції свідчить про тісний зв’язок між залежною і незалежними змінними. Стандартні помилки оцінок параметів моделі свідчать, що оцінки та є неефективними і зміщеними: стандартна помилка оцінки є майже такою, як і сама оцінка, а стандартна помилка оцінки у 1,5 раза перевищує цю оцінку. Звідси можна зробити висновок, що незважаючи на тісний зв’язок між змінними моделі, необхідно продовжити дослідження, перш за все збільшивши сукупність спостережень.

62. . Мультиколінеарність означає існування тісної лінійної залежності, або кореляції, між двома чи більше пояснювальними змінними.

Вона негативно впливає на кількісні характеристики економетричної моделі або робить її побудову взагалі неможливою.

Так, мультиколінеарність пояснювальних змінних призводить до зміщення оцінок параметрів моделі, через що з їх допомогою не можна зробити коректні висновки про результати взаємозв’язку залежної і пояснювальних змінних. У крайньому разі, коли між пояснювальними змінними існує функціональний зв’язок, оцінити вплив цих змінних на залежну взагалі неможливо.

Основні наслідки мультиколінеарності.

1. Падає точність оцінювання, яка виявляється так:

а) помилки деяких конкретних оцінок стають занадто великими;

б) ці помилки досить корельовані одна з одною;

в) дисперсії оцінок параметрів різко збільшуються.

2. Оцінки параметрів деяких змінних моделі можуть бути незначущими через наявність їх взаємозв’язку з іншими змінними, а не тому, що вони не впливають на залежну змінну. У такому разі множина вибіркових даних не дає змоги цей вплив виявити.

3. Оцінки параметрів стають досить чутливими до обсягів сукупності спостережень. Збільшення сукупності спостережень іноді може спричинитися до істотних змін в оцінках параметрів.

З огляду на перелічені наслідки мультиколінеарності при побудові економетричної моделі потрібно мати інформацію про те, що між пояснювальними змінними не існує мультиколінеарністі.

63 найпростіше позбутися мультиколінеарності в економетричній моделі можна, відкинувши одну зі змінних мультиколінеарної пари. Однак на практиці вилучення якогось чинника частосуперечить логіці економічних звязків.

Позитивно впливає на звільнення від мультиколінеарності суттєве збільшення сукупності спостережень, але цей підхід не завжди можна реалізувати на практиці. Можна також перетворити певним чином поянювальні змінні моделі:

А) знайти відхилення від середньої;

Б) замість абсолютних значень змінних обсичлити відності (етмпи зростання приросту.)

В) нормалізувати пояснювальні змінні

Г) використати «рідж-регресію»