31.Аналіз обмежень дефіцитних і недефіцитних ресурсів.

За допомогою двоїстих оцінок можна також визначити статус кожного ресурсу.

Ресурси, що використовуються для виробництва продукції, можна умовно поділити на дефіцитні та недефіцитні залежно від того, повне чи часткове їх використання передбачене оптима­льним планом прямої задачі. Якщо деяке значення двоїстої оцін­ки у_i в оптимальному плані двоїстої задачі дорівнює нулю, то відповідний i-й ресурс використовується у виробництві продукції не повністю і є недефіцитним. Якщо ж двоїста оцінка у_i > 0, то i-й ресурс використовується для оптимального плану виробницт­ва продукції повністю і називається дефіцитним. Відомо (третя теорема двоїстості), що величина двоїстої оцінки показує, наскі­льки збільшиться значення цільової функції Z, якщо запас відпо­відного ресурсу збільшити на одну умовну одиницю.

Статус ресурсів можна визначати трьома способами. Пер­ший — підстановкою значень вектора X* (оптимального плану виробництва) у систему обмежень прямої задачі. Якщо обмежен­ня виконується як рівняння, то відповідний ресурс дефіцитний, у іншому разі — недефіцитний:

Другий спосіб — через додаткові змінні прямої задачі. Якщо до­даткова змінна в оптимальному плані дорівнює нулю, то відповід­ний ресурс дефіцитний, а якщо більша від нуля — недефіцитний.

Третій спосіб — за допомогою двоїстих оцінок. Якщо у_i > 0, то зміна (збільшення або зменшення) обсягів i-го ресурсу приво­дить до відповідної зміни доходу підприємства, і тому такий ре­сурс є дефіцитним.

32.Аналіз коефіцієнтів цільової функції задач лінійного програмування.

Під впливом різних обставин ціна виробленої на підприємстві одиниці продукті може змінюватися (збільшуватися чи зменшуватися). І тому завжди цікаво і важливо знати у межах яких змін цін на продукцію кожного виду структура оптимального плану виробництва ще може залишатися такою самою тобто оптимальною (найкращою) навіть за цих певних змін

Перетворення симплексної таблиці за змін коефіцієнтів цільової функції стосуються лише елементів оцінкового рядка. Дослідимо питання зміни коефіцієнтів цільової функції для maxF=Σc_jx_j Нехай змiнюэться ціна на одиницю продукції виду С, тобто початкове знання З ум. од. подамо як 3 + ∆с₃, де ∆с₃ - величина зміни ціни одиниці продукції виду С.

Симплекс-таблиця, яка відповідає оптимальному плану, збері­гає свій вигляд за винятком елементів стовпчика «Сбаз» що, у свою чергу, впливає на значення всіх ненульових оцінок (Z_j – с_j).

Враховуючи систему нерівностей, нові значення оцінок мають задовольняти умову оптимальності, тобто Z_j – с_j >= 0.

Розрахунок інтервалів зміни значень коефіцієнтів цільової функції для небазисних змінних виконується згідно із співвід­ношенням -∞ <∆c_k ≤∆_k

Симплекс-таблиця, яка відповідає оптимальному плану, збері­гає свій вигляд за винятком ненульових значень оцінкового рядка (Z_j – с_j). Нові оцінки (Z_j – с_j) мають задовольняти умову оптима­льності задачі максимізації цільової функції, тобто бути не­від'ємними.

33.Цілочислове програмування. Область застосування цілочислових задач в плануванні й управлінні виробництвом.

Існує доволі широке коло задач математичного програмування, в економіко-математичних моделях яких одна або кілька змінних мають набувати цілих значень. Наприклад, коли йдеться про кількість верстатів у цеху, тварин у сільськогосподарських підприємствах тощо.

Зустрічаються також задачі, які з першого погляду не мають нічого спільного з цілочисловими моделями, проте формулюють­ся як задачі цілочислового програмування. Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування. У тому разі, коли цілочислових значень мають на­бувати не всі, а одна чи кілька змінних, задача називається частково цілочисловою.

До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).

Умови цілочисловості є по суті нелінійною і може зустрічатися в задачах, що містять як лінійні, так і нелінійні функції.

Загальна цілочислова задача лінійного програмування записується так:

max(min)F = Σ c_j х_j

за умов:

Σ a_ij х_j (≤,=, ≥)b_i (i=1,m)

х_j ≥0 (j=1,n)

х_j --цілі числа (j=1,n)

Область застосування цілочислових задач

Задача про рюкзак. Найпростішою задачею цілочислового програмування, а саме задачею лише з одним обмеженням, є за­дача про рюкзак (або ранець). Така задача має багато прикладів практичного застосування. Назва «задача про рюкзак» пов'язана з інтерпретацією задачі вибору найкращого складу предметів, що задовольняють певні умови гіпотетичної проблеми туриста щодо вибору для походу оптимальної кількості речей.

Турист може вибирати потрібні речі із списку з п предметів.

Відома вага кожного j-го предмета т_j (j =1,n). Визначена також цінність кожного виду предметів w_j .Максимальна вага всього вантажу в рюкзаку не може перевищувати зазначеного обсягу M. Необхідно визначити, скільки предметів кожного виду турист має скласти в рюкзак, щоб загальна цінність спорядження була max за умови виконання обмеження на вагу рюкзака.

Позначимо через х_j - кількість предметів j -го виду в рюкзаку. Тоді математична модель задачі матиме вигляд:

max F = Σ w_j х_j

Σ m_j х_j ≤ М

х_j ≥ 0, х _j — цілі числа, (j=1,n)

Задача оптимального розкрою матеріалів. На підприємстві здійснюється розкрій т різних партій матеріалів у обсягах b_i (і= 1, m) одиниць однакового розміру в кожній партії. Із матері­алів усіх партій потрібно виготовити max кількість комплектів Z, у кожен з яких входить р різних видів окремих частин в кількості k_r (r =1,р) одиниць, враховуючи, що кожну одиницю матеріалу можна розкроїти на окремі частини п різними способами, причому у разі розкрою одиниці і-ої партії j -им способом отримуємо а_іjr деталей r-го виду.

Запишемо математичну модель задачі. Позначимо через х_ij. кількість одиниць матеріалу i-ої партії, що будуть розкроєні j-тим способом. Тоді з i-ої партії за j-го способу розкрою отримаємo а_іjr х_ij деталей r-го виду. З усієї ж i-ої партії у разі застосування до неї всіх п способів розкрою отримаємо Σ а_іjr х_ij деталей r виду, а з усіх т партій їх буде отримано Z_r = Σ Σ а_іjr х_ij У кожен комплект має входити k_r(r = 1,р) деталей, тому відношення Z_r /k_r (r = 1,р) визначає кількість комплектів, які можна виготови­ти з деталей r-то виду. Кількість повних комплектів для всіх ви­дів деталей визначається найменшим з цих відношень.

У разі повного комплекту має виконуватися рівність відношень:

Z₁/k₁=Z₂/k₂=...= Z_r/k_r=... = Z_р/k_р,

звідки р - 1 відношення можна виразити через будь-яке з них, наприклад, через перше:

Z_r/k_r = Z₁/k₁ (r = 2,р) або Z_r = k_rZ₁ /k₁ (r= 2,р).

Замінивши Z_r та Z₁, їх значеннями, отримаємо р- 1 обмежен­ня стосовно комплектів:

Σ Σ а_іjr х_ij = k_r / k₁ Σ Σ а_іjr х_ij

Σ Σ (а_іjr k_r / k₁ а_іj1 ) х_ij =0, r=2,p

Враховуючи наявну кількість одиниць матеріалу в партіях, за­пишемо т обмежень щодо ресурсів:

Σ х_ij=b_i (i=1,m)

(Обмеження щодо використання ресурсів можуть бути рівняннями чи нерівностями залежно від того, повністю чи не пов­ністю необхідно використати наявний обсяг ресурсів).

Всі х_ij мають задовольняти умову невід'ємності:

х_ij≥ 0 (і=1,m; j=1,n) та цілочисловості.

Отже, необхідно знайти найбільше значення функції:

mахZ = min1/k_r Σ Σ а_іjr х_ij

з_а обмежень:

Σ Σ( а_іjr - k_r / k₁ а_іj1) х_ij=0, (r=2бз)

Σ х_ij = b_i (i=1,m)

х_ij≥ 0 (і=1,m; j=1,n)

х_ij — цілі числа (і=1,m; j=1,n).

Задача про призначення. Ця задача зводиться до транспортної і може бути розв'язана одним з відомих методів знаходження оптимального плану транспортної задачі. Проте такий вид задач належить до задач цілочислового програмування, оскільки їх змінні є бульовими і оптимальний план може бути знайденим також методами цілочис­лового програмування.

Задача планування виробничої лінії. Розглядається процес функціонування виробничої лінії. Відома схема, яка зображає послідовність робіт для виготовлення k видів продукції (k=1,К). Відомі також: a_j — тривалість виконання j-ї операції d_j^(k) _- термін для k-го виробу, до якого необхідно завершити операцію j; x_j — момент початку j-ї операції; t — тривалість ви­гнання всіх операцій. Допускається, що в будь-який момент на верстаті виконується тільки одна операція. Необхідно визначити оптимальні моменти початку кожної

операції.

Економіко-математична модель виробничої лінії міститиме такі групи обмежень:

1. Послідовність виконання j-ї операції записується для всіх пар операцій так: х_j+ а_j ≤ х_i (i,j = 1,п) якщо j-та операція передує і-й операції.

2. Обмеження щодо нерозгалуженості виробничого процесу для операцій i та j, які не виконуються одночасно (i≠j), має вигляд:

або х_і-x_j = а_j, якщо операція j передує операції i;

або x_j - х_і = а_i , якщо операція i передує операції j.

Зауважимо, що логічні обмеження виду «або-або» не можуть входити до економіко-математичної моделі задачі лінійного про­грамування, оскільки вони породжують неопуклу множину допу­стимих розв'язків. Тому необхідно ввести допоміжні змінні, які уможливлюють запис наведених вище логічних умов у вигляді лінійних обмежень. Це такі бульові змінні:

[0, якщо операція j передує і;

y_ij=

[ 1, якщо операція і передує j.

запишемо обмеження:

My_ij +(x_i-x_j) ≥a_j (i,j =1,n)

M (1-y_ij)+( x_j- x_i) ≥a_i (i,j =1,n)

Де М—досить велике число.

3. Обмеження щодо термінів виготовлення кожного виробу:

x_j+ a_j ≤ d_j^(k) (k=1,К)

де j—остання операція для k-го виробу.

4. Усі операції мають бути виконані до моменту t:

x_j+ a_j ≤ t ( j =1,n)

Критерії оптимальності:

min Z=t

Отже, маємо таку математичну модель:

min Z=t

x_j+ a_j ≤ x_j

My_ij +(x_i-x_j) ≥a_j (i,j =1,n; i≠j)

M (1-y_ij)+( x_j- x_i) ≥a_i (i,j =1,n; i≠j)

x_j+ a_j ≤ d_j^(k) (i =1,n ;k=1,К)

x_j+ a_j ≤ t ( j =1,n)

x_i(x_j ) ≥0 t≥0

y_ij≥0, y_ij –цілі числа (i,j =1,n)

Також існує задача з постійними елементами витрат та задача комівояжера.

34. Скажімо, множина допустимих розв’язків деякої нецілочислової задачі лінійного програмування має вигляд, зображений на рис Зауважимо, що геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі. Отже, для розглянутого випадку множина допустимих планів складається з дев’яти точок (рис. 6.2), які утворені перетинами сім’ї прямих, що паралельні осям Ох₁ та Oх₂ і проходять через точки з цілими координатами 0, 1, 2. Для знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій функції, пересуваємо у напрямку вектора нормалі до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний цілочисловий розв’я­зок відповідає точці М ( ).

Очевидно, особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.

35. Нехай маємо задачу цілочислового програмування Для її розв’язування можна скористатися ітеративним методом Гоморі. Суть його полягає ось у чому:

1. Знаходять розв’язок послабленої, тобто задачі без вимог цілочисловості змінних

Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є оптимальним планом задачі цілочислового програмування

2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:

,

де символ {} позначає дробову частину числа.

Для визначення дробової частини будь-якого числа від цього числа віднімають цілу його частину — найбільше ціле число, що не перевищує даного. Цілу частину числа позначають символом []. Наприклад,

[1,3] = 1; [–1,3] = –2;

{1,3} = 1,3 – 1 = 0,3; {–1,3} = –1,3 – (–2) =2 – 1,3 = 0,7.

3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Здобуту розширену задачу розв’язують, а далі перевіряють її розв’язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв’язку або доведено, що задача не має допустимих розв’язків у множині цілих чисел.

36. Досить детально розглянута в розділах, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на допущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Але такі зв’язки насправді є нелінійними, тому точніші математичні моделі доцільно формулювати в термінах нелінійного програмування.

І нарешті, будь-яка задача стає нелінійною, якщо в математич­ній моделі необхідно враховувати умови невизначеності та ризик.

Загальна задача математичного програмування формулюється так: знайти такі значення змінних x_j , щоб цільова функція набувала екстремального (максимального чи мінімального) значення:

за умов: ( ); .

Якщо всі функції та , є лінійними, то це задача лінійного програмування, інакше (якщо хоча б одна з функцій є нелінійною) маємо задачу нелінійного програмування.

Задачу нелінійного програмування намагаються звести до лінійного вигляду. Проте в такому разі можливі значні похибки. Нехай, наприклад, собівартість продукції y визначено як функцію , де х — обсяги виробництва. Ввівши заміну , дістанемо лінійну залежність . За такої заміни похибки немає. А коли , то заміна цієї залежності деякою лінійною функцією призводить до значних похибок

Отже, лінеаризація нелінійних процесів є досить складною математичною задачею.

Для задач нелінійного програмування не існує універсального методу розв’язування, тому щоразу слід доводити існування розв’язку задачі, а також його єдиність. Це досить складна математична задача.Відомі точні методи розв’язування нелінійних задач, але при цьому постають труднощі обчислювального характеру.

Для розв’язування нелінійних задач застосовують наближені методи, стикаючись із проблемою локальних і глобальних оптимумів. Більшість наближених методів дають змогу знаходити локальний оптимум. Визначивши всі локальні оптимуми, методом порівняння можна знайти глобальний. Звернемо увагу ще на один дуже важливий момент. У задачах лінійного програмування точка оптимуму завжди була граничною. Для нелінійних задач точка, яка є оптимальним планом, може бути граничною або такою, що міститься всередині допустимої області розв’язків (планів).

37. Геометрично цільова функція (8.1) визначає деяку поверхню, а обмеження (8.2)—(8.3) — допустиму підмножину n-вимірного евклідового простору. Знаходження оптимального розв’язку задачі нелінійного програмування зводиться до відшукання точки з допустимої підмножини, в якій досягається поверхня найвищого (найнижчого) рівня.

Якщо цільова функція неперервна, а допустима множина розв’язків замкнена, непуста і обмежена, то глобальний максимум (мінімум) задачі існує.

Найпростішими для розв’язування є задачі нелінійного програмування, що містять систему лінійних обмежень та нелінійну цільову функцію. В цьому разі область допустимих розв’язків є опуклою, непустою, замкненою, тобто обмеженою. .

38. Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування:

за умов

(6.16)

,де функції і диференційовані.

Ідея методу множників Лагранжа полягає в заміні даної задачі простішою: на знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і подається у вигляді:

(6.17)

де λ_і — не визначені поки що величини, так звані множники Лагранжа.

Знайшовши частинні похідні функції L за всіма змінними і прирівнявши їх до нуля:

запишемо систему

що є, як правило, нелінійною.

Розв’язавши цю систему, знайдемо і — стаціонарні точки. Оскільки їх визначено з необхідної умови екстремуму, то в них можливий максимум або мінімум.

39. Функція Лагранжа для цієї задачі має вигляд:

= . (8.12)

Точка називається сідловою точкою функції Лагранжа (8.12), якщо для всіх виконується співвідношення:

. (8.13)

Для диференційовних функцій та знайдемо необхідні умови існування сідлової точки.

Сідлова точка функції виду (8.12) за означенням задовольняє умову: .

Нерівність виконується для всіх точок Х, тобто також і для тих, у яких лише одна координата відрізняється від Х^*. Допустимо, що це х_k, а всі інші збігаються з координатами сідлової точки .

Об’єднуючи всі три випадки для невід’ємних координат, маємо необхідні умови сідлової точки:

для тих індексів j, де .(8.14)

для тих індексів j, де .(8.15)

, — довільного знака.(8.16)

.(8.17)

для тих індексів і, де ,(8.18)

для тих індексів і, де ,(8.19)

для тих індексів і, де має довільний знак.(8.20)

.(8.21)

Сукупність співвідношень (8.14)—(8.21) становить необхідні умови, які має задовольняти сідлова точка функції Лагранжа для точок, що належать множині . При цьому повинна мати частинні похідні по всіх компонентах векторів .

Теорема Куна—Таккера. Вектор Х^* є оптимальним розв’язком задачі (8.22)—(8.24) тоді і тільки тоді, коли існує такий вектор , що при для всіх точка є сідловою точкою функції Лагранжа , і функція мети для всіх угнута, а функції — опуклі

Доведення. Необхідність. Нехай Х^* — оптимальний план задачі (8.22)—(8.24), тобто є точкою глобального максимуму задачі. Отже, для всіх інших планів задачі Х з множини допустимих розв’язків виконуватиметься співвідношення:

.

Розглянемо тепер вектор , що відповідає точці глобального максимуму , і значення функції Лагранжа в точках , , , де — довільний план задачі з множини допустимих розв’язків, — вектор множників Лагранжа, що відповідає Х.

З умови (8.21) маємо: , тоді

.(8.25)

Для точки з координатами деякі доданки виду можуть бути відмінними від нуля. Оскільки за умовою задачі , то лише за умови, що , матимемо нерівність:

.

Функція — лінійна відносно , тобто остання нерівність виконується для будь-якого . Отже, точка — точка глобального мінімуму по функції Лагранжа.

Для встановлення нерівності, що відповідає лівій частині умови (8.13), а саме: , скористаємося також рівнянням (8.21), підсумувавши його по і: . За умовою теореми — угнуті функції і , тому виконується таке рівняння:

Отже, у точці Х^* функція Лагранжа має глобальний максимум по Х, що повністю доводить необхідність теореми.

Достатність. Для доведення достатності умов теореми потрібно виходити з того, що , — сідлова точка функції (тобто для виконується нерівність (8.13)), і необхідно довести, що тоді Х^* є оптимальним планом задачі опуклого програмування.

Підставимо у нерівність (8.13) вираз функції Лагранжа (8.12) для задачі (8.22)—(8.23):

(8.26)

при всіх значеннях .

Розглянемо праву частину подвійної нерівності (8.26).

.

Остання нерівність має виконуватися для всіх . Крім того, , тобто нерівність справджується лише у разі, коли

.

Тоді з лівої частини нерівності (8.26) маємо:

.

Через те що , приходимо до нерівності , яка справджується для всіх значень .

Отже, точка Х^* задовольняє обмеження і надає максимального значення цільовій функції задачі, тому що для всіх інших функція набуває менших значень, ніж у точці Х^*, тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов тереми доведено.

Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції.

40. Економетрія вивчає методи оцінювання параметрів економетричних моделей, які характеризують кількісні взаємо­зв’язки між економічними показниками, а також розглядає основні напрямки застосування цих моделей в економічних дослідженнях.

Економетрія поділяється на дві частини:

1) економетричні методи;

2) економетричні моделі економічних процесів і явищ.

У цьому курсі вивчатимемо здебільшого матеріал, що належить до першої частини, тобто економетричні методи. Економетричні методи можна умовно розбити на чотири групи. До першої групи входять методи оцінювання параметрів класичної економетричної моделі за методом найменших квадратів, їх верифікація. До другої групи належать методи оцінювання параметрів узагальненої моделі, коли порушуються деякі передумови використання методу найменших квадратів. До третьої групи входять методи оцінювання параметрів динамічних економетричних моделей, їх верифікація. Четверта група охоплює методи оцінювання параметрів економетричних моделей, які побудовані на основі системи одночасових структурних рівнянь.

41. Економетрична модель — це функція чи система функцій, що описує кореляційно-регресійний зв’язок між економічними показниками, один чи кілька з яких є залежною змінною, інші — незалежними

Побудова будь-якої економетричної моделі, незалежно від того, на якому рівні і для яких показників вона будується, здійснюється як послідовність певних кроків.

Крок 1. Знайомство з економічною теорією, висунення гіпотези взаємозв’язку. Чітка постановка задачі.

Крок 2. Специфікація моделі. Використовуючи всі ті форми функцій, які можуть бути застосовані для вивчення взаємозв’язків, необхідно сформулювати теоретичні уявлення і прийняті гіпотези у вигляді математичних рівнянь. Ці рівняння встановлюють зв’язки між основними визначальними змінними за припущення, що всі інші змінні є випадковими.

Крок 3. Формування масивів вихідної інформації згідно з метою та завданнями дослідження.

Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів, що дає змогу проаналізувати залишки і відповісти на запитання: чи не суперечить специфікація моделі передумовам “класичної” моделі лінійної регресії?

Крок 5. Якщо деякі передумови моделі не виконуються, то для продовження аналізу треба замінювати специфікацію або застосовувати інші методи оцінювання параметрів.

Крок 6. Проведення аналізу вірогідності моделі та визначення прогнозу за побудованою моделю.

42. Навіть побіжне знайомство з економічними показниками, взаємозв’язок між якими вимірюється, показує, що окремі експериментальні значення залежної змінної не можуть міститися строго на прямій лінії чи на графіку функції іншої форми. Певна частина фактичних спостережень над змінною лежатиме вище або нижче від значень, обчислених згідно з вибраною функцією. Якщо фактичні значення залежної змінної містяться на значній відстані від обчислених з допомогою функції, то можна припустити, що формалізація залежності між економічними показниками на основі функції типу (2.15) чи якоїсь іншої функції не адекватна реальному процесу взаємозв’язків в економіці. Проте поняття «значна відстань» не є конкретним, а тому не може бути критерієм для оцінювання адекватності моделі.

Щоб розв’язати цю задачу, до економетричної моделі вводять стохастичну складову, яка акумулює в собі всі відхилення фактичних спостережень змінної Y від обчислених згідно з моделлю.

Математичний аналіз цієї складової дасть змогу зробити висновок щодо того, чи можна вважати її стохастичною і чи містить вона систематичну частину відхилень, яка може бути зумовлена наявністю тих чи інших помилок у моделюванні.

43,47 Розглянемо економетричну модель з двома змінними у загальному вигляді: Y = f(X) + u, (2.15)

де Y — залежна змінна; X — незалежна змінна; u — випадкова складова.

Це означає, що ми ідентифікували змінну X, яка впливає на змінну Y. Назвемо таку економетричну модель простою моделлю.

Як відомо, численні взаємозв’язки між економічними показниками не можна формалізувати лише на базі простої економетричної моделі. Наведені раніше приклади економетричних моделей показують, що вони описують вплив багатьох чинників на економічні процеси та явища. Причому для формалізації цих зв’язків може використовуватись не одне рівняння, а їх система.

На базі простої економетричної моделі розглянемо принципову структуру економетричної моделі та основні методи оцінювання її параметрів. Змістовне тлумачення взаємозв’язку між економічними показниками [модель (2.15)] має підказати його конкретну аналітичну форму. Але оскільки одні й ті самі економічні умови можуть задовольняти різні функції, то краще звернутися до статистичного аналізу і з його допомогою зробити вибір серед можливих альтернативних варіантів.

Найпростішою є лінійна форма зв’язку між двома змінними:

Y = a₀ + a₁X ,

де a₀ і a₁ — невідомі параметри, перший з яких визначає довжину відрізка, утворюваного перетином прямої з віссю ординат, а другий — тангенс кута нахилу цієї прямої до осі абсцис.

Можливі й інші форми залежностей між двома змінними, наприклад:

Останнє з цих співвідношень є лінійним відносно , а перші два можна звести до лінійної форми для перетворених змінних, якщо взяти логарифми від виразів в обох частинах кожного з рівнянь:

lnY = lna₀ + a₁X;

lnY = lna₀ + a₁lnX.

44,46 Принцип найменших квадратів відхилень полягає в знаходженні таких і , для яких найменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметрів і . Метод, який реалізує принцип найменших квадратів, називається методом найменших квадратів (1МНК) Зауважимо, що ІМНК доцільно застосовувати коли залишки розподілені нормально тобто коли середнє їх значення дорівнює нулю і дисперсія стала.

,

45 ??? Запишемо систему рівнянь у матричному вигляді АХ = В, де

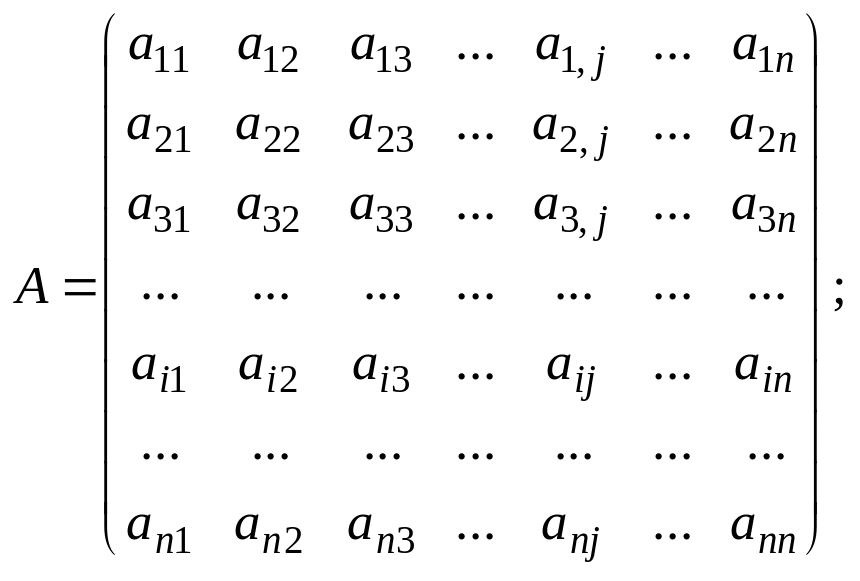
Матриця А є квадратною порядку n; вектор-стовпець Х має розмір n × 1; вектор-стовпець В — порядок n × 1.

Якщо матриця А невироджена, тобто rgA = n і , то система лінійних рівнянь має єдиний розв’язок виду

Розглянемо однорідну систему лінійних рівнянь:АХ = 0

Нехай А — квадратна матриця n-го порядку; Х — вектор-стовпець розміру n × 1.

Тривіальний розв’язок має вигляд: . Нетривіальний розв’язок може існувати лише за умови, що визначник матриці А дорівнює нулю:

Коли це так, то система матиме безліч розв’язків. Їх можна нормувати, вимагаючи, наприклад, щоб виконувалася рівність

48. Перша умова, здавалося б, є очевидною. Адже коли математичне сподівання залишків не дорівнює нулю, то це означає, що існує систематичний вплив на залежну змінну, а до модельної специфікації не введено всіх основних незалежних змінних. Якщо ця передумова не виконується, то йдеться про помилку специфікації.

Друга умова передбачає наявність сталої дисперсії залишків. Цю властивість називають гомоскедастичністю. Проте вона може виконуватись лише тоді, коли залишки u є помилками вимірювання. Якщо залишки акумулюють загальний вплив змінних, які не враховані в моделі, то звичайно дисперсія залишків не може бути сталою величиною, вона змінюється для окремих груп спостережень. У такому разі йдеться про явище гетероскедастичності, яке впливає на методи оцінювання параметрів.

Третя умова передбачає незалежність між залишками і пояснювальними змінними, яка порушується насамперед тоді, коли економетрична модель будується на базі одночасових структурних рівнянь або має лагові змінні. Тоді для оцінювання параметрів моделі використовуються, як правило, дво- або трикроковий метод найменших квадратів.

Четверта умова означає, що всі пояснювальні змінні, які входять до економетричної моделі, мають бути незалежними між собою. Проте очевидно, що в економіці дуже важко вирізнити такий масив незалежних (пояснювальних) змінних, які були б зовсім не пов’язані між собою. Тоді щоразу необхідно з’ясовувати, чи не впливатиме залежність пояснювальних змінних на оцінку параметрів моделі.

Теорема Гаусса — Маркова. Функція оцінювання за методом 1МНК покомпонентно мінімізує дисперсію всіх лінійно незміщених функцій вектора оцінок : для ,

де — дисперсія оцінок , визначених згідно з 1МНК, — дисперсія оцінок , визначених іншими методами.Отже, функція оцінювання 1МНК у класичній лінійній моделі є найкращою (мінімально дисперсійною) лінійною незміщеною функцією оцінювання.

49. незміщена оцінка дисперсії залишків:

, де n – кількість спостережень, m – кількість змінних у моделі..Оскільки вектор залишків , то добуток векторів можна записати так:

.Звідси маємо альтернативну форму запису дисперсії залишків: