68. Неодн. Лин. Ду n-го порядка с пост. Коэф-тами, спец. Прав. Часть.

Лин. неодн. ур-е -го порядка имеет вид

(1)

где , - непр-ны на инт-ле .

Общее реш-е ур-я (1) нах-ся по ф-ле (2)

- общее реш-е лин. одн. ур-я , соответствующего ур-ю (1), а - к-нибудь частное реш-е неодн. ур-я (1)

Опр. ФСР – любые лин. независимых реш-й ур-я .

1. Если сущ. ФСР, то общ. реш-е неодн. ур-я (1) м. б. найдено с пом Метода вариации произвольных постоянных (Лагранжа).Сущность этого метода сост. в след. Общее реш-е неодн. ур-я (1) ищем в виде (3)

где ф-и опр-ся из сист. ур-й

(4Относ. (4) явл. сист. лин. неодн. алгебраич. ур-й, причем главный определитель сист.

(5)

Поэтому сист. (4) имеет единств. реш-е:

, (6)

откуда (7)

где - произвольные постоянные. Учитывая рав-ва (3) и (7), общее реш-е неодн. ур-я, найденное методом вариации произвольных постоянных, получаем в виде

(8)

2. Метод неопр коэф-тов.

Пусть , где , - многочлен степени .

1)Если не совпадает ни с одним корнем х-кого ур-я. Тогда

,

где - многочлен той же степени, что и .

2)Если совпадает с корнем х-кого ур-я кратности . Тогда

,

где - многочлен той же степени, что и .

Пусть

1) - не явл. корнем х-кого ур-я

где - многочлен той же степени, что и .

2) - явл. корнем х-кого ур-я

69. Лінійні неоднорідні диференціальні рівняння 2го порядку зі сталими коефіцієнтами. Метод варіації довільних сталих.

Уравнение вида

,

где , - функция от и , называется неоднородным диф-ным ур-нием 2го порядка с постоянными коэффициентами.

Метод вариации произвольных постоянных используется для нахождения частного решения лин. неоднороднного диф. ур. 2-го порядка с постоянными коэффициентами, при любом виде правой части . Суть решения:

1. Отыскивается общее решение соответствующего однородного уравнения ( т.е. ):

.

2. Частное решение неоднородного диф. ур. ищется в виде:

(т.е. заменяются на функции времени ).

3. Функции ( ) определяются из системы:

.

4. Общее решение неоднородного ур. Определяется в виде суммы: общего решения однородного ур. и частного решения неоднородного ур. :

.

Пример:

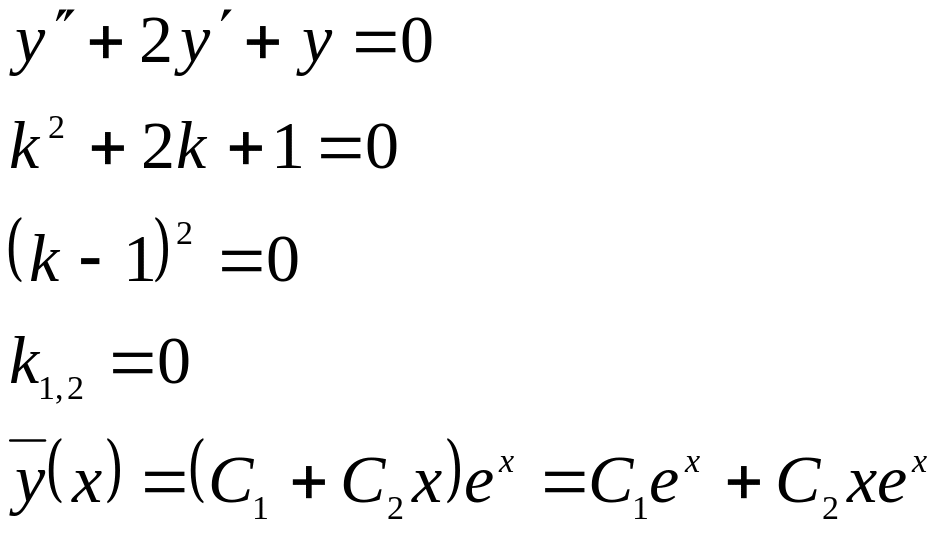
Пусть

Определим неизвестные ф-ции и из системы:

Решаем систему по методу Крамера:

Общее решение

.

70. Лінійні однорідні диференціальні рівняння 2го порядку зі сталими коефіцієнтами. Узагальнення на випадок рівняння -го порядку.

Уравнение вида

(1)

где (действительные), называется лин. однородным ур. 2го порядка с постоянными коэффициентами.

Для нахождения решения ур. (1) составляется характеристическое ур. вида:

(2)

и определяются корни данного квадратного уравнения, которые называются характеристическими числами. Структура общего решения ур (1) зависти от вида корней ур. (2).

1-ый вид: Корни действительные и различные , тогда общее решение ур. (1) имеет вид:

2-ой вид: Корни комплексно сопряженные , тогда общее решение ур. (1) имеет вид:

3-ий вид: Корни действительные и кратные(равные) , тогда общее решение ур. (1) имеет вид:

4-ый вид: Корни комплексно сопряженные кратные(равные) , тогда ур. (1) имеет вид:

.

Узагальнення на випадок рівняння -го порядку.

Уравнение вида

(3)

где (действительные), называется лин. однородным ур. -го порядка.

Для нахождения решения ур. (3) составляется характеристическое ур. вида:

(4)

и определяются корни его корни, , которые называются характеристическими числами. Структура общего решения ур. (3) зависит от вида корней ур. (4).

1-ый вид: Корни действительные и различные , тогда общее решение ур. (3) имеет вид:

2-ой вид: Корни комплексно сопряженные , тогда общее решение ур. (3) имеет вид:

3-ий вид: Корни действительные и кратные(равные) , тогда общее решение ур. (3) имеет вид:

4-ый вид: Корни комплексно сопряженные кратные(равные) , тогда ур. (3) имеет вид:

.