Если рассмотрим обе формулы площадей вместе, получим
.
Площадь плоской фигуры.
ОПР: Плоская фигура – замкнутая и огр. множ. т. плоскость.
ОПР: множ. т. плоскости наз. огр. если найдется круг с кон. радиусом содержащий это множ.
OR(Mo)={M E2|p(M,Mo)<R} – открытый круг с центром в т. Мо и радиусом R
ОПР: Окрестность т. Мо это окрестность круга с центром в Мо
ОПР: т. Мо {X} является внутренней этого множ. если найдется ε-окрестность в т. Мо которая принадлежит этому множ. Множ. всех внутренних т. Х наз. внутренностью и ОБ: intX = (a;b)
ОПР: т. Мо наз. граничащей т. Х если в любой ее ε-окрестности содержатся как т. из множ. Х так и не принадлежащие ему. Множ. всех граничных т. Х наз. границей множ. и ОБ: δХ
ОПР: Множ. Х наз. открытым если оно состоит только из внутренних т. т.е. intX=X
ОПР: Множ. Х наз.
замкнутым если его дополнение открыто
или содержит свою границу δХ
Х
ОПР: б.говорить, что плоские фигуры G и G’ равны если сущ. биекция F которая отображает одни т. фигуры на другие с сохранением расстояния между т.
М – площадь 1) M(G)≥0; 2) M(G+G’)=M(G)+M(G’) , G∩G’=0
ОПР: Многоугольник – плоская фигура огр. одной или несколькими замкнутыми ломанными.
Рассмотрим произвольную плоскую фигуру Ф и рассмотрит множ. всех многоугольников описывающих ( содержащих ) Ф, ОБ: Р* и множ. всех вписанных ( содержащихся ) в Ф ОБ Р*.
Р
М(Р)≤М(Ф)
≤М(
)
Множ. всех площадей Р* - ограниченно снизу, множ. всех площадей Р* - ограничено сверху. =>
infM(P*)=(об)=М*(Ф) , supM(P*)=(об)=М*(Ф)
М*(Ф) – б.наз. верхней площадью фигуры Ф или внешней мерой Жордана.
М*(Ф) – б.наз. нижней площадью фигуры Ф или нижней мерой Жордана.
УТВ: любая плоская фигура имеет внешнюю и внутреннюю меры Жордана.
ОПР: Фигура Ф наз. квадрируемой или измеримой по Жодрану если внешняя М*(Ф)=М*(Ф)=(об)=М(Ф)
ОПР: б.говорить, что площадь фигуры Ф = 0, Ф имеет площадь меры 0, если ее можно покрыть многоугольниками сколь угодно малой площади.
Т1: Ф – плоская фигура квадрируема когда М(δФ)=0.
Т»: Ф – плоская фигура квадрируема если ее граница является спрямляемой.
ЗАМ: Можно разбить
плоскость на квадратики ( одинаковые
) площадью δ и в качестве Р*=Σ всех
квадратиков которые имеют с Ф хотя бы
одну т., Р*
- множ. всех квадратиков которые не
содержат ни одной общей т. с дополнением
к Ф. При измельчении разбиения площади
( т.е. ум↓δ ) М(Р*) ум↓, а М(Р*)
ув↑ =>
Площадь криволинейной трапеции
Пусть f(x)≥0 на [a;b] и f(x) – непрерывна
1)Покажем что Ф – квадрируема. разобьем [a;b] произвольным образом
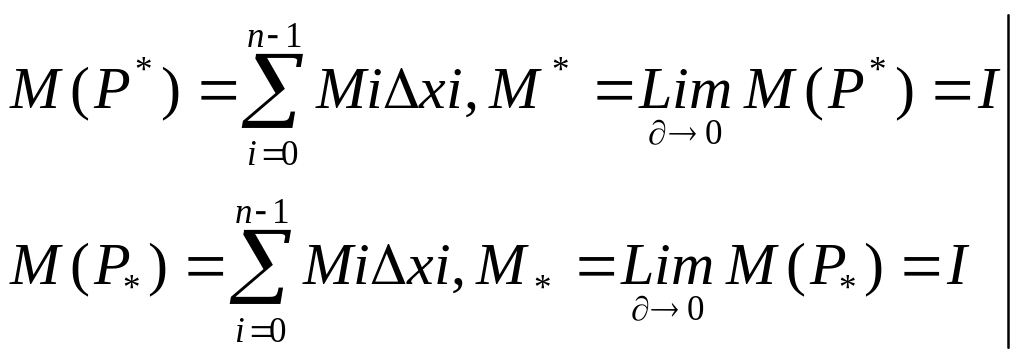т.к. f
– интегрируема [a;b]
=> по ОПР. Ф – квадрируема
2)Вычислим М(Ф)=М*=М*=
ЗАМ: Если f(x)≥g(x)≥0
на [a;b]
и f(x),g(x)
– интегрируема на [a;b],
то площадь фигуры огр. f(x),
g(x)
х=а, х=b
выч. по формуле
Площадь криволинейного сектора
ОПР: Криволинейный сектор – плоская фигура огр. лучами φ=α, φ=β и кривой r=r(φ)
Зададим разбиение м={ φi } т.е. α=φ0<φ1<φ2<…<φn= β. Построим вписанные и описанные сектора. В каждом криволинейном секторе из разбиения выберем mi=infr(φ), φ[φ1, φi+1] и mi=supr(φ), φ[φ1, φi+1]
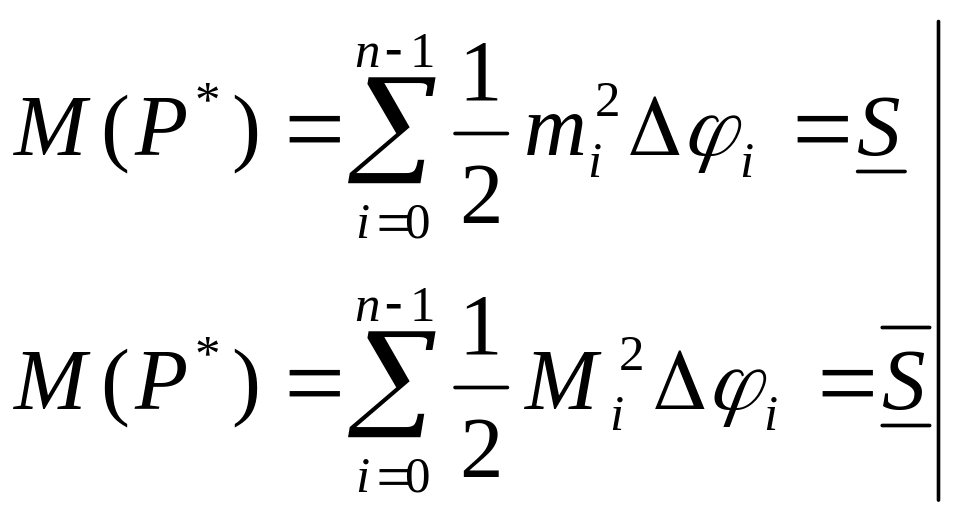где
- суммы Дарбу функции
Если r(φ)
– непрерывна на [a;b]
=(по Т.)=> она интегрируема и
интегрируема на [a;b]
=(по критерию Дарбу)=>
и
т.е. фигура является квадрируемой и
