1.ОПР. Функция F(х) называется первообразной функцией для функции f(x) на интервале (а,b), если в любой точке х интервала ( а,b) функция F(x) дифференцируема и имеет производную F’(x),равную f(x).
УТВ. Если на некотором числовом промежутке I(x) F’(x)=0 для любых х1, х2 и F(x) непрерывна и дифференцируема ,то
F(x)=const.
ДОК: По т. Лагранжа т.к. непрерывна и дифференцируема на числовом промежутке I(x), то найдется с, что
(f(x1)-f(x2))/(x1-x2)=F’(c) ,а т.к. F’(c)=0,тo F(x1)-F(x2)=0,т.е.
F(x1)=F(x2) значит F(x)=const.
СЛЕД : Если на промежутке для функции f(x) имеется две первообразные F1(x),F2(x),то они отличаются на соnst.
ДОК:(F1(x)-F2(x))’=F1’(x)-F2’(x)=f(x)-f(x)=0 .Отсюда
F1(x)-F2(x)=c, т.к. только производная от const ровна нулю.
ОПР. Совокупность всех первообразных функций для данной функции f(x) на интервале (a,b) называется неопределенным интегралом от функции f(x) и обозначается символом ∫f(x)dx
(∫-знак интеграла,f(x)dx–подынтегральное выражение ,
f(x) – подынтегральная функция).
2.СВОЙСТВА:
1.d∫f(x)dx=f(x) док. dF(x)=F’(x)dx=f(x)dx
2.∫dF(x)=F(x)+c, c=const док. dF(x)=f(x)dx
3.Интеграл от суммы двух интегралов равен сумме интегралов каждой из двух функции : ∫(af(x)+bf(x))dx=∫af(x)dx+∫bf(x)dx=a∫f(x)dx+b∫f(x)dx.
док. Дифференцируем:
d∫(af(x)dx+b(x))=(af(x)+bf(x))dx=af(x)dx+bf(x)dx=d(a∫f(x)+b∫f(x))=da∫f(x)dx+db∫f(x)dx=af(x)+bf(x).
В ряде случаев в качестве новой переменной лучше выбрать t=u(x).
3. 1. интегрирование заменой переменной. Пусть функция определена и дифференцируема на множестве {х}, представляющем собой либо интервал , либо полупрямую, либо бесконечную прямую и пусть {t} множество всех значений этой функции и пусть для f(x) существует на множестве {t} первообразная F(x),т.е.∫f(t)dt=F(t)+c. Тогда всюду на множестве {x} для функции f(u(x))u’(x) существует первообразная функция равная F(u(x)),т.е.
∫f(u(x))u’(x)dx=F(u(x))+c.
Непосредственное интегрирование-интегрирование по таблице и по свойствам.
4.2. интегрирование по частям. ∫u’vdx=vu-∫uv’dx,где v,u дифференцируемы на множестве {x}.
Рассмотрим:
UV=∫(UV)’DX=∫(U’V+V’U)DX=∫U’VDX+∫V’UDX=∫VDU+∫UDV
UV=∫VDU+∫UDV, ∫VDU=UV-∫UDV.
5.Разложение на простые дроби. Pn(X)/Qm(X)
Если
D<0
(p^2+px+q)
комплексные корни.
Замечание: Будем рассматривать такие дроби что n<m так как n>=m можно поделить столбиком многочлен Pn на Qm и выделив рациональную и еще дробную часть.
Др/рациональное выражение Pn(x)/Qm(x) Теорема Др/рациональные выражения (1) при выполнении (2)единство образов можно расположить на сумму дробей
Ai,Mi,Ni
(принадлежат) R
и находятся единственным образом.
Алгоритм вычисления дробно рациональных функций. Gk(x)/Qm(x)
Если k>=m то необходимо выделить целую часть.
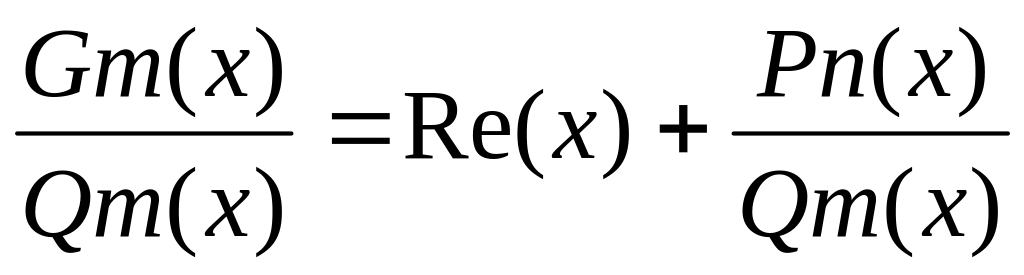n<m
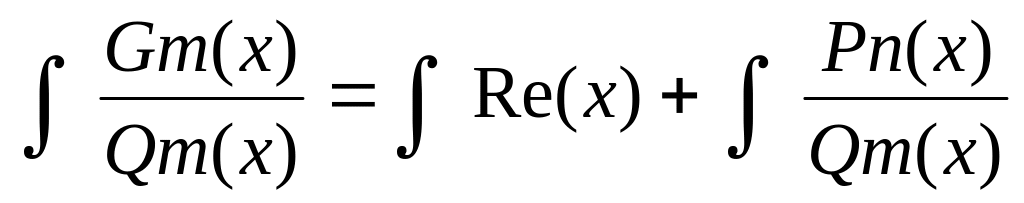вычислить по
таблице.Расписать на простейшие дроби. По Т и найти Ai, Mi, Ni
Вычислить интеграл от простейшей дроби.
Пусть Pn(x)/Qm(x) правильная рациональная дробь или просто рациональная дробь , тогда deg(Pn(x))=n, deg(Qm(x))=m, где Qm,Pn-многочлены.
Рассмотрим два случая:
1.n>m ,тогда делим числитель на знаменатель и получаем интеграл от числа и дроби ,которая будет являться правильной ;
2.n<m
Рассмотрим Qm(x)=(x-a)ªw(x);Pn(x)/Qm(x)-правильная дробь, Qm имеет вещественное число а корнем кратности a ,w(a)≠0.
Тогда для этой дроби справедливо следующее представление:
Pn(x)/Qm(x)=A/(x-a)ª+r(x)(x-a)٩/(x-a)ª w(x).
Где А-вещественная постоянная, равная P(a)/w(a),٩-целое число:
٩>= 1,r(x) –некоторый многочлен с вещественными коэффициентами ,такой что вторая дробь правильная.
ДОК. Рассмотрим разность P(x)/Q(x) – A/(x-a)ª , приводя эту разность к общему знаменателю, будем иметь:
P(x)/Q(x) – A/(x-a)ª = (P(x)/Q(x) – Aw(x))/(x-a)ªw(x)=Ф(x)/(x-a)ªw(x);
Ф(x)=P(x)-Aw(x)
Т.к. Ф(a)=P(a)-Aw(a)=P(a)w(a)/w(a)=0 , вещественное число а является корнем многочлена Ф(x) некоторой кратности ٩>=1 .
Это значит что справедливо представление:
Ф(x)= (x-a)٩r(x),где r(x)-некоторый многочлен с вещественными коэффициентами.
Подставляя в первое равенство, имеем:
Re[P(a)/w(a)] – A/(x-a)ª =(P(x)/Q(x) – Aw(x))/(x-a)ªw(x)=
(x-a)٩ r(x)/(x-a)ªw(x);
Тем самым представление доказао.
Пусть теперь Qm(x) имеет комплексные числа a=u+iv,
a”=u-ivкорнями кратности a ,т. е.
Q(x)=(x-(u+iv))(x-(u-iv))ªw(x)= (x²+px+q)ªw(x),w(a)≠0,w(a”)≠0,
p=-2u,q=u²+v².
Тогда для дроби справедливо следующее представление:
P(x)/Q(x)= (Mx+N)/ (x²+px+q)ª + r(x) (x²+px+q)٩/ (x²+px+q)ªw(x),(**)
Где M,N –некоторые вещественные постоянные, ٩-целое число >=0, r(x)-некоторый многочлен с вещественными коэффициентами, такой что вторая лробь является правильной .
Обозначим Re[A] –действительная часть числа А,Im[A] –мнимая, положим :
M=(1/u) Re[P(a)/w(a)], N=Re[P(a)/w(a)]-u/v Im[P(a)/w(a)],
нетрудно проверить,что M,N являются решениями
P(a)-(Ma+N)w(a)=0.
В самом деле ,поделив это уравнение на w(a) и приравняв к нулю мнимую и действительную части мы получим два равенства
Mu+N= Re[P(a)/w(a)], Mv= Re[P(a)/w(a)].Рассмотрим разность
P(x)/Q(x)- (Mx+N)/ (x²+px+q)ª
приводим к общему знаменателю :
P(x)/Q(x)- (Mx+N)/ (x²+px+q)ª=(P(x)-(Mx+N)w(x)) /
(x²+px+q)ªw(x)=Ф(x)/ (x²+px+q)ªw(x). (*)
Равенство позволяет утверждать, то комплексное число а и а” являются корнями многочлена некоторой кратности ٩>=1 .В таком случае для Ф(x) справедливо представление:
Ф (x)= (x²+px+q)٩r(x), r(x) -некоторый многочлен с вещественными коэффициентами ,не имеющих своими корнями а и а”.
Вставляя Ф(х) в(*) получим (**).Тот факт ,что последняя дробь в (**) правильная вытекает из того .что эта дробь равна разности двух правильных дробей .Утверждение доказано.
b1 b2 bm a
Пусть Q(х) =(x- d1) (x- d2) …(x-dm) ( x²+p1x+q1) …
n
( x²+pnx+qn )
Тогда для нее по предыдущим утверждениям справедливо следующее разложение:
(1) (1) 2 (1) b1 (m)
P(x)/Q(x)=B1 /(x-d1) +B2 /(x-d2) +…+Bb1/(x-d1) +B1/(x-dm)
(m) 2 (m) bm (1) (λ)
+B2/Bbm(x-dm) +Bbm/(x-dm) +…+(M1x+N1 )/ ( x²+p1x+q1)+
(1) (1) 2 (1) (1) λ1
M2 x+N2/ ( x²+p1x+q1) +…+ Mλ1x+Nλ1/ ( x²+pnx+qn) +
(n) (n) (n) (n) 2
(M1x+N1)/ ( x²+pnx+qn)+( M2x+N2 )/ ( x²+pnx+qn) +
(n) (n) λn (1) (1) (m) (1) (2) (1) (n) (n)
(Mλnx+Nλn1)/ ( x²+p1x+q1) ,B1 ,B2 ,Bbm ,M1 ,M1 ,N1 ,Mλn, Nλn-
-некоторые вещественные постоянные ,часть из которых может быть равна нулю.Существует четыре типа простейших интегралов.
1.∫dx/(x-x0) ДОК.∫ dx/(x)=∫dx/(x-x0)=ln(x-x0)
2.∫dx/(x-x0)ⁿ ДОК.∫ dx/(x-x0)ⁿ=∫ d(x-x0)/(x-x0)ⁿ=-1/ ((n-1)(x-x0) )n-1
3.∫dx/(ax²+bx+c) ДОК.∫ dx/(ax²+bx+c)=1/a∫dx/( x²+b/a x+c/a)=
1/a∫dx/((x+b/2a)²+c/a-b²/4a²)=1/a∫dt/t²+d²=1/ad²∫dt/( t²/ d² + 1)=
1/ad∫d(t/d)/( t²/ d² + 1)=1/ad∫dz/(z²+1)=1/ad arctg(t/d)+c=
(1/( c/a-b²/4a²))arctg((x+b/2a)/(c/a- b²/4a²))
4.∫dx/(ax²+bx+c)ⁿ ДОК.∫(ex+f)dx/(ax²+bx+c)ⁿ=1/aⁿ∫ (ex+f)dx/(x²+b/a x+c/a)ⁿ=
1/aⁿ∫ (ex+f)dx/((x+b/2a)²+c/a - b²/4a²)ⁿ=
e/aⁿ∫ (x+f/e)dt/(t²+d²)ⁿ=
e/aⁿd²ⁿ∫(t_b/2a+e/f)dt/( t²/ d²+1)ⁿ= ∫(Ax+B)dx/(x²+1)ⁿ=A∫xdx/(x²+1)ⁿ +B∫ xdx/(x²+1)ⁿ =- a(x²+1)/2(n-1)(x²+1)ⁿ+B∫dx/(x²+1)ⁿ+c
∫ dx/(x²+1)ⁿ= ∫ d(x²-x²+1)/(x²+1)ⁿ= ∫ dx/(x²+1)ⁿ+ ∫ x² dx/ (x²+1)ⁿ -
∫ x² dx/(x²+1)ⁿ=I(n-1)-∫ x² dx/(x²+1)ⁿ =
I(n-1)-1/2∫xd(-(x²+1)/(x²+1)ⁿ(n-1))=I(n-1)+1/2(n-1)∫(x(x²+1)/ (x²+1)ⁿ -∫(1+x²)dx/ (x²+1)ⁿ)=I(n-1)+x(x²+1)/2(n-1) (x²+1)ⁿ-I(n-1)/2(n-1)
I(n)=I(n-1)((2n-3)/2(n-1))+ x(x²+1)/2(n-1) (x²+1)ⁿ