6.Метод Остроградского.

М.В.Остроградский предложил метод выделения рациональной части интеграла от правильной рациональной дроби P(x)/Q(x).

Анализируя виды интегралов можно сделать следующие выводы

1. ∫dx/(x-x0), ∫(Mx+N)dx/(x-x0)-

знаменатели которых содержат двучлен или трехчлен являются нерациональными функциями(они равны ln или arctg).

2. ∫adx/(x-x0)ⁿявляется правильной рациональной дробью со знаменателем ,равным тому же двучлену в степени (n-1).

3. ∫(Mx+N)dx/(x-x0)ⁿ - равен сумме правильных рациональных дробей со знаменателем в степени (n-1) и приводящихся к арктангенсу от интеграла вида ∫dx/(ax²+bx+c).

Эти выводы позволяют заключить .что рациональная часть всего интеграла от P(x)/Q(x) , которая не сократима .Пусть Q(х) имеет вид d1 dm a1 an

(x-b1) …(x-bm) (x²+p1x+q1) … (x²+pnx+qn)

Тогда рациональная часть интеграла от P(x)/Q(x) равна сумме правильных рациональных дробей ,знаменатели которых соответственно равны

d1-1 dm-1 a1-1 an-1

(x-b1) …(x-bm) (x²+p1x+q1) … (x²+pnx+qn)

Рациональная часть интеграла от P(x)/Q(x) представляет собой правильную рациональную дробь P1(x)/Q1(x) ,где Q1(x) имеет вид

d1-1 dm-1 a1-1 an-1

(x-b1) …(x-bm) (x²+p1x+q1) … (x²+pnx+qn)

Посчитаем сумму тех дробей ,интегралы от которых представляют собой нерациональные функции. Из 1. и 3. следует, что эта сумма равна правильной рациональной дроби P2(x)/Q2(x),

Q2(x)= (x-b1) …(x-bm) (x²+p1x+q1) … (x²+pnx+qn)

Т.о. мы приходим к следующей формуле

∫ dxP(x)/Q(x)= P1(x)/Q1(x) +∫ P2(x)/Q2(x),

Q1(x) – НОД(Q(x),Q’(x)),

Q2(x)=Q(x)/Q1(x)

P1(x)-многочлен с неопределенными коэффициентами степени на 1 меньше, чем степень Q1(x),

P2(x)-многочлен с неопределенными коэффициентами со степенью на 1 меньше, чем степень Q2(x).

Для вычисления неопределенных коэффициентов следует продифференцировать формулу Остроградского, привести результат дифференцирования к общему знаменателю и сопоставить коэффициенты при одинаковых степенях х в числителях.

8.Интегрирование биноминальных дифференциалов.(Подстановка Чебышева) Выражение x^m(a+bx^n)^p*dx-биноминальный дифференциал m,n,p (принад.) Q, a,b(принадл) R

Теорема Чебышева: Для того что бы было интегрировано в конечном виде необходимо и достаточно что бы имел место 1 из 3 случаев p(прин) Z, m+1/n (принадл) Z, (m+1)/n +p (принадл) Z

1) -Первая подстановка Чебышева.(p)

2) m+1/n

3) m+1/n +p

При помощи подстановок Чебышева вычисляются интегралы от дифференциального бинома . Будем рассматривать случай, когда n, m и p – рациональные, а a и b – вещественные числа.

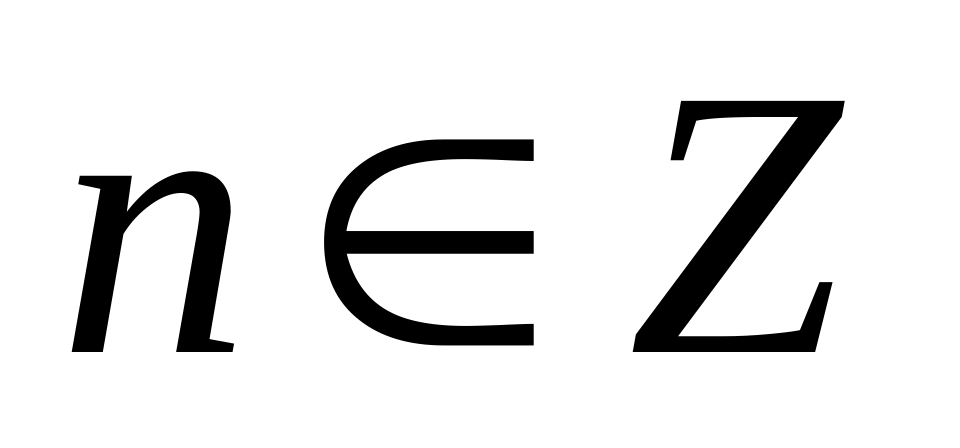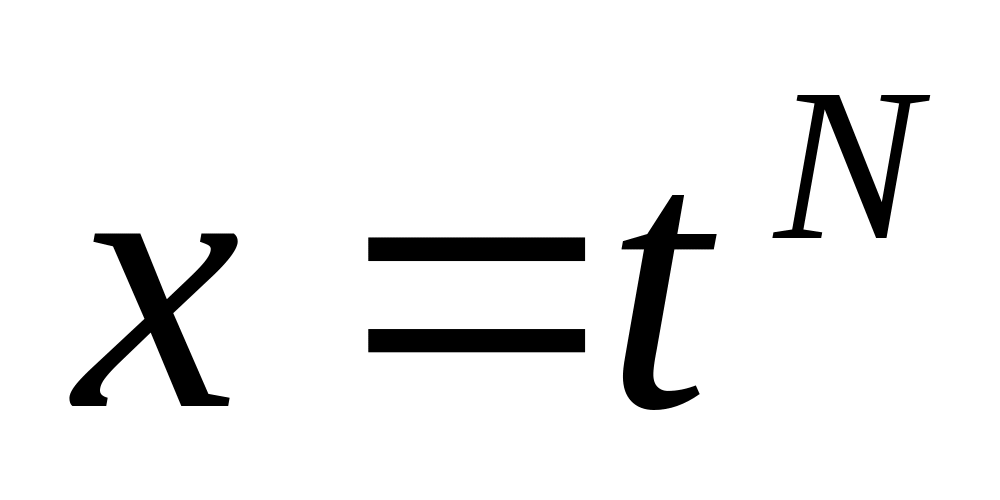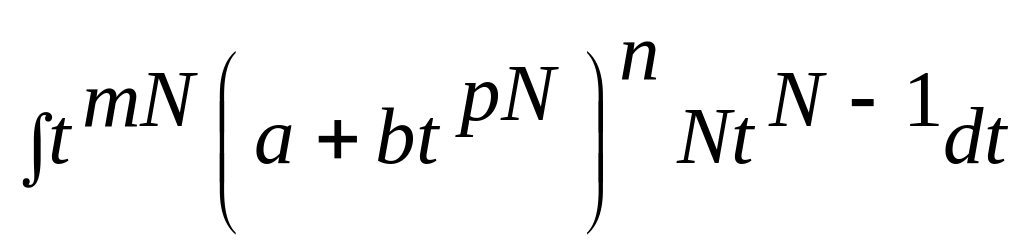1. . Сделаем замену , где N – наименьшее общее кратное m и p. Получим интеграл от рациональной дроби.

2. _{. При подстановке , где N*n – целое число, получим .}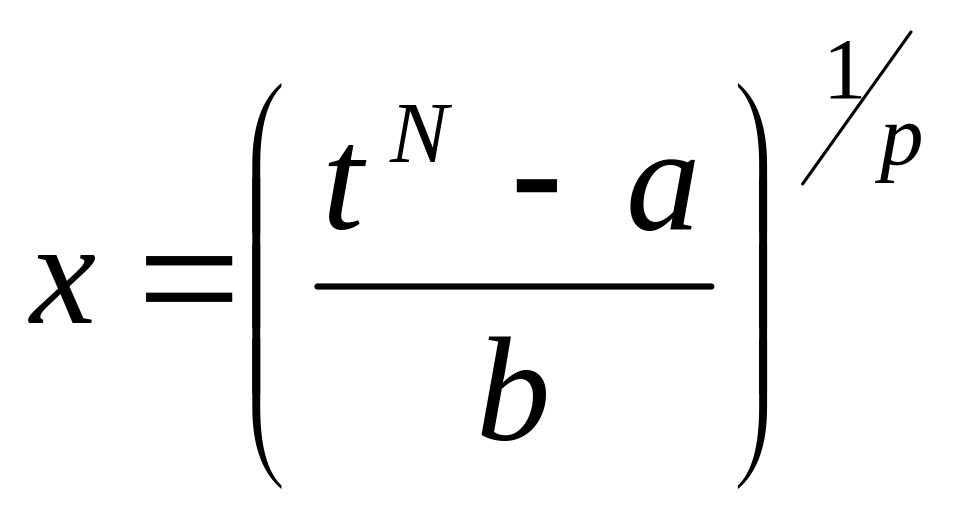

_{Отсюда получим , если степень , т.е. - целое число, получим интеграл от рациональной дроби.}

_{3. .Преобразуем интеграл:}

_{. Сделаем подстановку , где N*n – целое число. Тогда .Получим интеграл}

_{, данный интеграл будет интегралом от рациональной дроби, если степень , т.е. - целое число.}

_{П.Л. Чебышев показал, что при показателях m, n и p, не удовлетворяющих вышеуказанным условиям, интеграл от дифференциального бинома не выражается через элементарные функции.}