2.6. Уравнение изотермы химической реакции. Химическое сродство
Направление самопроизвольного протекания химической реакции определяется убылью соответствующего термодинамического потенциала, а глубина протекания абсолютной величиной этой убыли, т.е. максимальной полезной работой.
Преобразуем уравнение (107)
(107)
к виду:
.
Заменим дифференциалы частными приращениями:
.
Получим уравнение
для стандартного изменения
,
когда
.
Выразив химический потенциал компонента
через его парциальное давление
,
для реакции (106) запишем:
.
После преобразований получим:
,
(115)
где – исходные (или неравновесные) парциальные давления реагирующих веществ.
Так как при
:
,
то
.
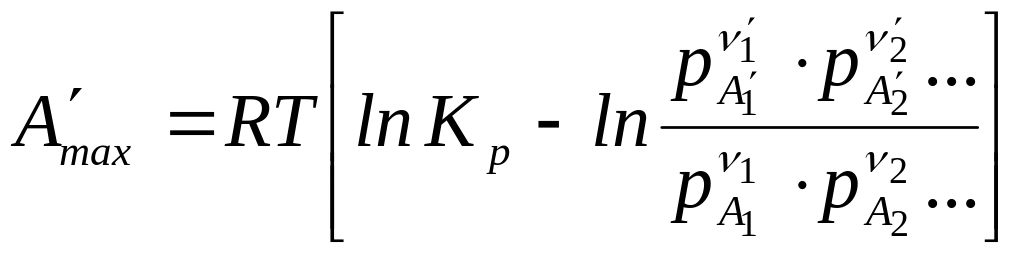(116)
Аналогично для
реакции, протекающей при
,
,
получим:
;
(117)
,
(118)
где
– исходные (или неравновесные) концентрации
реагирующих веществ.
Уравнения (115, 117) – называют уравнениями изотермы химической реакции (изотермы Вант–Гоффа), а (116, 118) – уравнениями максимальной работы химической реакции.
Абсолютные значения
изменения термодинамических потенциалов
показывают, насколько далека система
от состояния химического равновесия.
Чем меньше
,
тем ближе система к состоянию равновесия.
В предельном случае когда
– в системе химическое равновесие.
Поэтому величины
,
или максимальную работу процесса
называют мерой химического
сродства.
На основе уравнения изотермы химической реакции можно рассчитать максимальную работу и предсказать направление самопроизвольного протекания химической реакции. Напомним, что если
,
,
то
процесс протекает самопроизвольно в
сторону образования продуктов реакции;
,
,
то
процесс протекает в сторону образования
исходных веществ;
,
,
то
система находится в состоянии равновесия.
Для сравнительной
оценки химического сродства различных
химических реакция определяют стандартную
энергию Гиббса
(энергию Гельмгольца
)
или стандартное
химическое сродство
– химическое сродство реакции, протекающей
в стандартных условиях (при парциальных
давлениях реагирующих веществ
= 1):
.
(119)
Аналогично для реакции, протекающей при :
.
(120)
Для идеальных
растворов в уравнении изотермы химической
реакции константу равновесия выражают
с помощью мольных долей (
).
Для реальной газовой смеси – с помощью
фугитивностей (
)
(уравнение 121), а для реальных растворов
– с помощью термодинамических активностей
(
)
(122).
,
(121)
.
(122).
2.7. Влияние температуры на константу химического равновесия (уравнения изобары и изохоры химической реакции)
В качественной форме смещение равновесия описывается принципом Ле-Шателье: если на систему, находящуюся в устойчивом равновесии оказать внешнее воздействие, то равновесие сместится в направлении процесса, течение которого ослабляет влияние произведенного воздействия.
Пусть химическая реакция (106) протекает в идеальной газовой фазе. Тогда при стандартная максимальная работа химической реакции:
.
(119)
Максимальная работа процесса в соответствии с уравнением Гиббса–Гельмгольца:
.
(85)
Продифференцируем уравнение (119) по температуре:
.
(123)
Подставим в
уравнение (85) вместо
и
их значения из (119) и (123), получим:
.
Преобразуем:
.
(124)
Аналогично при :
.
(125)
Уравнения (124) и (125) называют уравнениями изобары и изохоры химической реакции. Они характеризуют влияние температуры на константу химического равновесия.
Уравнения изобары
и изохоры позволяют спрогнозировать
изменение константы химического
равновесия при изменении температуры.
Знак производной, стоящей в левой части
уравнений, а, следовательно, и направление
изменения
при изменении
определяется знаком теплового эффекта
химической реакции. Если:
– для эндотермической
реакции константа химического равновесия
возрастает с увеличением температуры.
Химическое равновесие смещается в
сторону увеличения выхода продуктов
реакции (
);
– для экзотермической
реакции
убывает с увеличением температуры.
Химическое равновесие смещается в
сторону уменьшения выхода продуктов
реакции (
);
– температура не
влияет на
.
Разделим переменные в уравнении изобары
.
(126)
1.
Проинтегрируем в небольшом температурном
интервале, считая, что
не зависит от температуры:
.
(127)
Применяя уравнение
(127), можно рассчитать средний тепловой
эффект реакции
,
если известны значения констант
равновесия в узком интервале температур
или рассчитать
,
если известно
и средняя величина теплового эффекта
реакции в интервале температур от
до
.
ЛЕКЦИЯ 8
2. Проинтегрируем уравнение изобары (126) в неопределенных пределах (от абсолютного 0 до ) с учетом температурной зависимости :
.
где
– тепловой эффект реакции при абсолютном
нуле температур.
.
В результате получим:
,
(128)
где
– константа интегрирования.
Для расчета константы равновесия необходимо определить численное значение . Для конденсированных систем в области температур, прилегающих к абсолютному нулю, эта задача была решена на основе тепловой теоремы Нернста.
Конденсированными называют системы, не изменяющие своего агрегатного состояния при охлаждении до абсолютного нуля (кристаллические вещества).
С помощью III закона термодинамики можно показать, что для реакций, протекающих в конденсированных системах константа интегрирования в уравнении (128) равна нулю. Тогда
.
Для реакций,
протекающих в идеальной газовой фазе
.
На основе тепловой теоремы Нернста–Планка
получено следующее уравнение для
константы интегрирования:
,
где
– химическая постоянная вещества;
– стехиометрический
коэффициент.
Суммирование проводится по всем газообразным веществам, принимающим участие в реакции.
Например:
;
.
Тогда для газообразных систем уравнение для константы равновесия имеет вид:
.