Взаимосвязь энергии гельмгольца с другими термодинамическими функциями и параметрами состояния системы

1) продифференцируем уравнение (76):

.

Подставим в полученное уравнение вместо его значение из уравнения (71), получим:

;

.

Поскольку изменяется при изменении объема и температуры, то есть , то и называют собственными параметрами состояния системы для свободной энергии Гельмгольца.

Если : уравнение устанавливает связь с ;

: уравнение устанавливает связь с .

Функцию, производная которой выражает другую термодинамическую функцию или параметр состояния, называют характеристической функцией.

Таким образом, свободная энергия Гельмгольца является характеристической функцией.

2) применим теперь уравнение (76) к начальному (₁) и конечному (₂) состояниям системы в каком-либо изохорно-изотермическом процессе:

; .

Вычтем почленно, получим:

(78) уравнение Гиббса – Гельмгольца, позволяющее определить возможность протекания изохорно-изотермического процесса

Перепишем уравнение Гиббса – Гельмгольца (78) в виде:

,

подставим вместо , и их значения:

; ; .

После подстановки, получим:

(79) уравнение максимальной работы Гиббса – Гельмгольца

В уравнении (79): – тепловой эффект изохорно-изотермического процесса – и – легко рассчитываются.

Следовательно, подставляя их значения в уравнение можно определить идет реакция или нет. Максимально возможный выход будет при равновесии.

Когда прямой ход реакции;

обратный ход реакции;

термодинамическое равновесие.

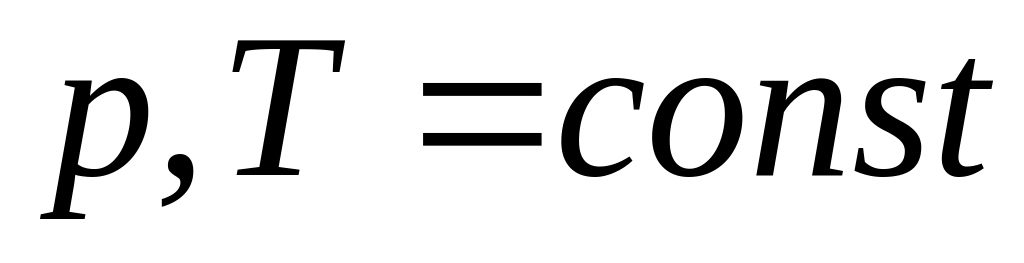4. (изобарно-изотермический процесс) (их большинство)

Для анализа воспользуемся выражением (74), получим:

или ;

;

. (80)

Функция обладает всеми свойствами термодинамической функции состояния. – энергия Гиббса (свободная энтальпия) – пятая термодинамическая функций состояния.

Получаем:

.

Знак неравенства характеризует условие самопроизвольного (необратимого) протекания изобарно-изотермического процесса. Как видно, таким условием является убыль энергии Гиббса.

( ).

Равновесие в системе при изохорно-изотермических условиях устанавливается при минимальном значении энергия Гиббса. Условием минимума функции и, следовательно, равновесия является:

.

Применим теперь к анализу обратимого изобарно-изотермического процесса уравнение (71), получим:

.

После интегрирования имеем:

. (81)

Как видим, убыль энергии Гиббса в изобарно-изотермическом процессе характеризует его максимальную работу.

Таким образом, энергия Гиббса является изобарно-изотермическим термодинамическим потенциалом.

Взаимосвязь энергии гиббса с другими термодинамическими функциями и параметрами состояния системы

1) подставив в уравнение (80) значение энтальпии :

,

получим:

. (82)

Для 1 моль идеального газа , следовательно

.

Из анализа последнего уравнения видно, что если идеальный газ взят при абсолютном нуле температур, то , а и одинаковы.

2) продифференцировав уравнение (82), получим:

.

Так как ,

. (83)

Поскольку изменяется при изменении давления и температуры, т.е. , то и являются собственными параметрами состояния системы энергии Гиббса.

Если : уравнение устанавливает связь с ;

: уравнение устанавливает связь с .

Таким образом, энергия Гиббса является характеристической функцией.

3) запишем уравнение (80) последовательно для исходного (₁) и конечного (₂) состояния системы в каком-либо изобарно-изотермическом процессе:

; .

вычтем почленно из последнего уравнения предыдущее и получим вторую форму записи уравнения Гиббса – Гельмгольца:

(84) Уравнение Гиббса – Гельмгольца, позволяющее определить возможность протекания изобарно-изотер-мического процесса (применяется чаще, чем первая)

Перепишем уравнение Гиббса-Гельмгольца (83) в виде:

.

подставим в (83) вместо , и их значения:

; ; .

После подстановки, получим:

(85) уравнение максимальной работы Гиббса-Гельмгольца

Когда прямой ход реакции;

обратный ход реакции;

условие термодинамического равновесия в системе при .

Вывод: есть пять критериев направления самопроизвольного протекания процессов и равновесия в системах ( и 4 термодинамические потенциала)

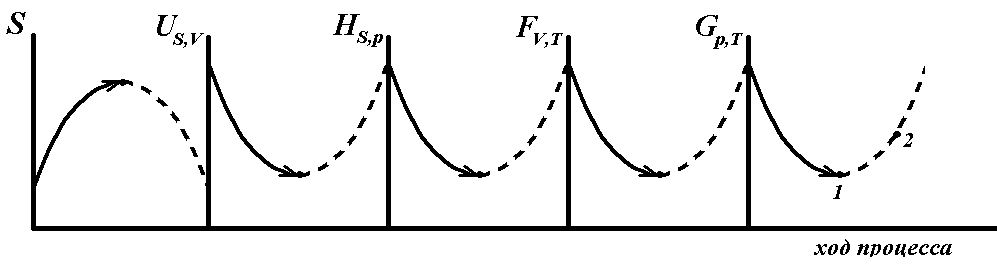
Рис. 9. Изменение энтропии , – , – , – , – потенциалов в ходе процесса: самопроизвольный процесс; --- – несамопроизвольный процесс

Система	Условие самопроизвольного протекания процесса	Условие равновесия	Условие экстремума
Изолированная		,
Любая		, , , ,