1.8. Взаимосвязь энтропии и термодинамической вероятности

В классической термодинамике состояние термодинамических систем описывается с помощью небольшого числа макроскопических параметров ( , , , ), доступных непосредственному измерению. Указанные параметры характеризуют макроскопическое состояние системы. Так как система состоит из микрочастиц, то макроскопические параметры обладают статистической природой и характеризуют средние свойства большого числа микрочастиц.

В статистической термодинамике микросостояние термодинамических систем характеризуют микроскопическими параметрами – координатами молекул ( , , ), определяющими их положение в пространстве, и импульсами движения молекул , характеризующими энергию их движения.

Одно и тоже макросостояние системы может быть реализовано большим числом различных микросостояний.

Число микросостояний, реализующих данное макросостояние системы, Больцман назвал термодинамической вероятностью . Чем больше , тем вероятнее пребывание системы в данном состоянии.

В статистической термодинамике предполагают, что процесс, приближающий систему к состоянию равновесия, соответствует переходу от менее вероятного состояния к более вероятному. Процесс, удаляющий систему от состояния равновесия, с точки зрения статистической термодинамики не является невозможным, просто он менее вероятен.

Таким образом, самопроизвольные процессы в изолированных системах характеризуются увеличением, как ее энтропии, так и термодинамической вероятности системы. Связь между энтропией и термодинамической вероятностью выражается уравнением Больцмана:

, (67)

где – постоянная Больцмана.

Уравнение Больцмана лежит в основе современной статистической термодинамики, связывает макро- и микропараметры системы и позволяет понять свойства энтропии как функции состояния.

При абсолютном нуле температур в системе абсолютный порядок ( ) и энтропия . При нагревании системы возникает тепловое движение, упорядоченность в системе уменьшается, энтропия возрастает. При смешивании упорядоченность в системе может, как увеличиваться, так и увеличиваться. Таким образом, энтропия – мера беспорядка в системе.

ЛЕКЦИЯ 5

1.9. Термодинамические потенциалы и направление самопроизвольных процессов. Условие термодинамического равновесия в системе

Термодинамическими потенциалам называют такие термодинамические функции состояния, убыль которых в обратимо протекающих процессах при постоянстве определенных параметров равна максимальной полезной работе процесса.

Для того, чтобы получить представление о термодинамических потенциалах воспользуемся совместным математическим выражением I и II законов термодинамики. Получим его:

уравнение I закона термодинамики (6)

или уравнение II закона термодинамики (49)

Из сравнения уравнений (6) и (49) следует:

(68) для обратимых и необратимых процессов

(69) для обратимых процессов полезная работа максимальна

(70) для обратимых и необратимых процессов, если единственной работой процесса является работа расширения

(71) для обратимых процессов, если единственной работой процесса является работа расширения

Известно, что . Продифференцируем уравнение и решим его относительно , получим:

.

Подставим в уравнения (68) – (71) вместо его значение, получим:

(72) для обратимых и необратимых процессов

(73) для обратимых процессов полезная работа максимальна

(74) для обратимых и необратимых процессов, если единственной работой процесса является работа расширения

(75) для обратимых процессов, если единственной работой процесса является работа расширения

Воспользуемся выражениями (68) – (75) для анализа некоторых термодинамических процессов.

1. (изохорно-изоэнтропийный процесс)

Рассмотрим процесс, единственным результатом которого является работа расширения. Из выражения (70) имеем:

; .

Знак неравенства относится к самопроизвольно протекающему (необратимому) изохорно-изоэнтропийному процессу, знак равенства характеризует термодинамическое равновесие.

Таким образом, получили, что выражение ( ), т.е. убыль внутренней энергии системы, характеризует условие самопроизвольного протекания изохорно-изоэнтропийного процесса. Как только внутренняя энергия достигает своего минимального значения устанавливается термодинамическое равновесие. Условие минимума внутренней энергии системы при :

.

Из уравнения (69) получаем:

;

.

Как видим, уменьшение внутренней энергии системы в изохорно-изоэнтропийном процессе характеризует максимальную работу этого процесса.

Таким образом, внутренняя энергия является изохорно-изоэнтропийным термодинамическим потенциалом.

2. (изобарно-изоэнтропийный процесс)

Из выражения (74) имеем:

; .

Знак неравенства характеризует условие самопроизвольного протекания (необратимого) изохорно-изоэнтропийного процесса. Как видно, таким условием является уменьшение энтальпии системы.

( ).

При установившемся термодинамическом равновесии в системе при энтальпия системы минимальна. Условие минимума функции:

.

Используем теперь для анализа обратимого изобарно-изоэнтропийному процесса уравнение (73), которое перепишется в виде:

;

.

Как видим, уменьшение энтальпии системы в изобарно-изоэнтропийном процессе характеризует максимальную работу этого процесса.

Таким образом, энтальпия является изобарно-изоэнтропийным термодинамическим потенциалом.

Рассмотренные процессы на практике реализуются крайне редко. Поэтому материал имеет в большей степени теоретическое, чем практическое значение. Большинство же реальных процессов, протекающих в природе, технологии реализуются либо при , либо при . Рассмотрим эти процессы.

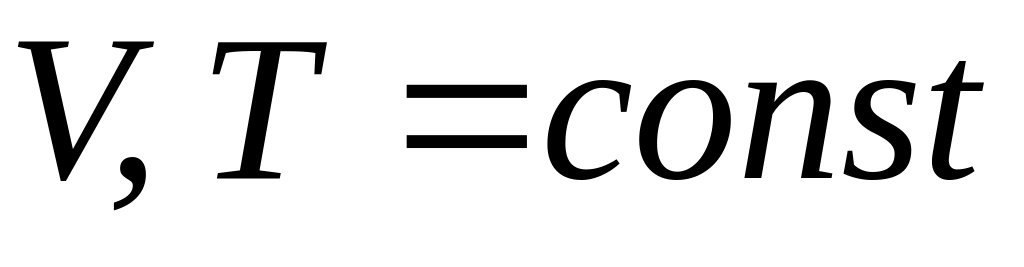3. (изохорно-изотермический процесс)

Для анализа воспользуемся выражением (70), тогда имеем:

или ;

.

Слева полный дифференциал, следовательно, изменение функции

. (76)

не зависит от пути протекания процесса, а определяется только начальным и конечным состояниями системы. Кроме того, функция аддитивная, так как составляющие ее функции аддитивные. Следовательно, функция обладает всеми свойствами термодинамической функции состояния. – функция (или энергия) Гельмгольца (свободная энергия) – одна из важнейших функций состояния.

; .

Знак неравенства характеризует условие самопроизвольного (необратимого) протекания изохорно-изотермического процесса. Как видно, таким условием является убыль энергии Гельмгольца.

При термодинамическом равновесии энергия Гельмгольца системы в изохорно-изотермических условиях минимальна. Условие минимума функции:

.

Воспользуемся теперь уравнением (69) для анализа обратимого изохорно-изотермического процесса, получим:

.

После интегрирования имеем:

. (77)

Как видим, уменьшение энергии Гельмгольца системы в изохорно-изотермическом процессе характеризует максимальную работу процесса.

Таким образом, энергия Гельмгольца является изохорно-изотермическим термодинамическим потенциалом.

Решим (76) относительно :

,

где – полная внутренняя энергия системы, складывается из 2 частей:

– свободная энергия – часть внутренней энергии, которая может быть превращена в работу (см. уравнение (77));

– связанная энергия – часть внутренней энергии, которая не может быть превращена в работу. Она обеспечивает существование самой материальной системы.