25.Застосування інтегрального числення до розв-ня задач геометрії і фізики.

1. Площа фігури.

В Декартові системі координат за основну фігуру, площа якої виражається одним інтегралом, приймають криволінійну трапецію. Якщо – рів-ня лінії, яка обмежує трапецію, то площа трапеції S:

, де a i b – межі інтегрування – абсциси початку і кінця лінії.

Якщо лінія , то здійснюючи підстановку в інтегралі, отримаємо:

, де – значення, між якими змінюється параметр t , коли точка пробігає зліва направо всю лінію, яка обмежує трапецію зверху.

В полярних координатах

2. застосування кратних інтегралів до обчислення об’ємів тіл.

Нехай маємо просторове тіло Т. а) Нехай відомий поперечний переріз просторового тіла в будь-якій точці, переріз тіла перпендикулярний до осі ОХ.

, де S(x) – площа поперечного перерізу у т. х, перпендикулярній до осі ОХ.

б) Нехай маємо циліндричний брус. Об’єм його знаходиться за формулою: . Це одна задач, що приводить до поняття подвійного інтеграла.

в) Об’єм тіла за допомогою потрійного інтеграла обчислюється за ф-лою: .

Справді нехай маємо просте тіло Т. Розіб’ємо його сіткою інтегральних поверхонь на частинні тіла і складемо інтегральну суму для ф-ції f(x,y,z)≡1 по тілу Т: .

Перейдемо в даній рівності до границі, коли . Тоді границя інтегральної суми дасть потрійний інтеграл, а границя сталої V буде сама стала. Маємо:

3. Довжина дуги.

Довжиною дуги кривої лінії назив. границя, до якої прямує довжина вписаної в неї ламаної при необмеженому зростанні числа її ланок і при прямуванні довжини найбільшої ланки до нуля.

Нехай лінія АВ задана р-ням: y=f(x).

Тоді :

4.Кординати центра мас і статичні моменти.

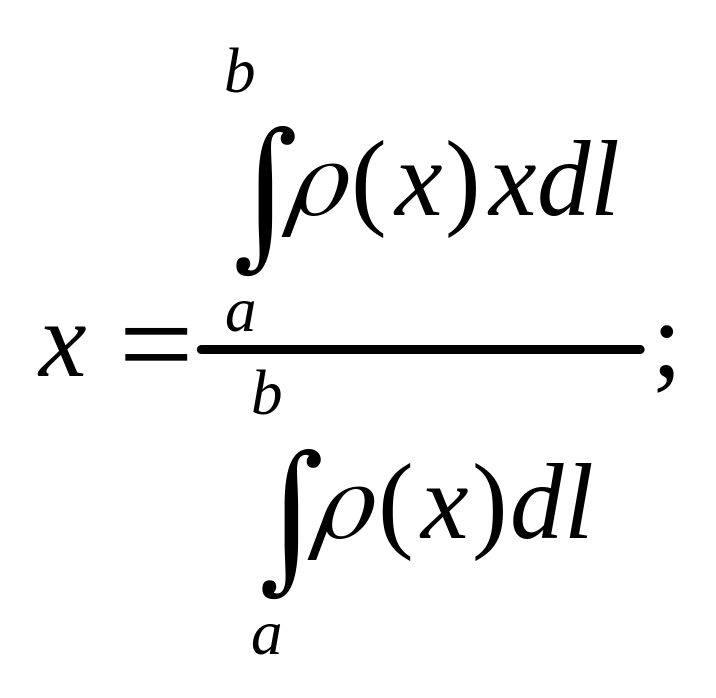
де матеріальної кривої, – диференціал дуги.

Якщо , то .

Ф-ли для статичних моментів:

, якщо то: .

5. Обчислення роботи, яку виконує змінна сила:

26. Обернені тригонометричні функції дійсної та комплексної змінної (означення, властивості).

Нехай дано функція y=sinx. Область її визначення – всю числову вісь розіб’ємо на інтервали монотонності, яких є нескінченне число:

Виберемо в якості основного інтервал і функцію, обернену до функції y=sinx, позначимо через y=arcsinx. Так як множина значень функції y=sinx – інтервал [-1;1], то цей же інтервал є областю визначення функції y=arcsinx, а множина її значень – інтервал Отже, Значення функції arcsinx – це радіанна міра кута, синус якого дорівнює даному значенню незалежної змінної х, із всіх кутів, які задовольняють цю умову, вибирається кут, який знаходиться в межах від до Таким чином рівність y=arcsinx еквівалентна двом наступним:

Будуючи за звичайним правилом графік оберненої функції, тобто за допомогою відображення відносно бісектриси 1-го і 3-го координатних кутів, отримаємо графік функції y=arcsinx. З графіка видно, що y=arcsinx – зростаюча і непарна (arcsin(-x)=-arcsinx).

Утворюючи на кожному із вказаних вище інтервалів монотонності відповідну обернену функцію, ми отримаємо нескінченне число однозначних віток; всі вони визначені на інтервалі [-1;1]. Перша функція друга Всю сукупність однозначних віток позначають через Ця функція нескінченнозначна, бо воан складається з нескінченного числа однозначних віток. Зображаючи їх всі на графіку, ми отримаємо ту ж синусоїду, тільки по-іншому розташовану відносно осей координат.

Зазвичай маємо справу з віткою її наз. головним значенням функції .

Обернені тригоном. функції комплексної змінної.

Поряд з головними значеннями arc-ів розглядають многозначні функції. Arccos z і Arcsin z і розв’язком рівняння cos z=a буде z=Arccos a.

Якщо тригонометричне рівняння має дійсні корені, то використовуючи многозначні функції Arc-ів ці дійсні корені одержуються: