In metres.

The computations can be checked by deriving the heights of

points b, с and d from using the adjusted hu . The resulting values

must not differ from the adjusted values EL , H and H_Л.

bed

6.4.7 Variance-Covariance Matrix of the Parametric Adjustment Solution Vector, Variance Factor and Weight Coefficient Matrix

The parametric adjustment solution vector X is given by equation (6.77), i.e.

T -1 T - -1 T

X = (A PA) A PL = (N A P) L

This can he written as:

X = В L

(6.81:

■where

-1 T В = N A P •

(6.82)

The variance-covariance matrix E* of the solution vector X can be easily

x

deduced by applying the covariance law (equation (6.15)) on (6.8l)j we get:

^EX ^{= BE}L (6.83)

From equation (6.66), we have

P = кЕг-""*¹

Ju

and inverting both sides we obtain

= к P""¹ . (6.Qk)

Substituting (6.82) and (6.81+) into (6.83) we get

E* = (N^wlA^TP) к P™¹ (N^P)*. (6.85)

л.

Both P and N are symmetric matrices, so that we can write:

T Т т m i

P = P, N = N and (1 ) = N .

Substituting this into (6.85) we get

-1 T -1 -1

= к N A P P P. A N

X

= к N""¹ (A^TPA) if¹ = к N~¹ N if¹ = к N""¹ ,

that is

E~ = к jf¹ = ic (А^АГ¹

(6.86)

On the other hand, by putting P •= кЕ-"^-1 in (6.86) we get

1»

^JX

z,: = - к (a^t г-Л)"¹ = (a^te_f*¹a)*¹ ,

ic L L '

(6.87:

which shows that does not depend on the choice of the factor к. In fact,

this statement is valid only if we know the correct values of the elements

of Е- . Unfortunately₅ however, £- is often known only up to a scale factor. L li

I.E. We know the relative variances and covariances of the observations only. This means that we have to work with the weight matrix к£- 1

without knowing the actual value of the factor к. Therefore cannot be

jL

computed from equation (6.87).

^ЛТ ^л

If we develop the quadratic form V pv 3) considering the obser­vations l to be influenced by random errors only, we get an estimate к for the assumed factor к given by

V^Tpv = (n - u) к . (6.88)

The multiplier in the right-hand side is nothing else but the difference between the number of independent observations and the number of unknown parameters, i.e. the number of redundant observations, which is sometimes denoted by'cif^and called the number of degrees of freedom, i.e.

df = n - u . (6.89)

df must be greater than zero in order to be able to perform a least-squares adjustment. Hence equation (6.88) becomes

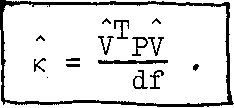
(6.90)

Usuallyj in the literature, к is known as the a priori variance factor and к is called the least-squares estimate of the variance factor^or,simply» estimated or a posteriori variance factor. ФЬе estimated variance factor can be now used instead of the a priori one, yielding an estimate of E^.

-1 а Т -1 = к N = к(A PA)

X

(6.91)

which is known as the estimated variance-covariance matrix of X.

To discuss the influence of the chosen variance factor к in

the weight matrix P = к Е-¹ on E", as defined by (6.91), we take another

L X

factor, say к¹. We obtian P¹ = к'Е- ¹ = yP. Substituting in equation

L

(6.91) we get:

^ ₌ Y (V^TPV) 1 _(AT_pA)-l ₌

^hX df у X "

The above result indicates that 2> given by equation (6.91) is independent

of the choice of the a priori variance factor к. We recall that the same

a

holds true for the estimated solution vector X (equation 6.79).

It often happens in the adjustment calculus, that we have to use

the estimated parameters X in subsequent adjustments as "observations".

Then we have to take into account their respective weights. We know that

the weight matrix of an observation vector must be proportional to the

inverse of its variance-covariance matrix (equation 6.66). Thus, we can

weight matrix of the vector X, since the inverse N is proportional to the variance-covariance matrix E^. Accordingly, the matrix N ¹ is known also as the weight coefficient matrix and the square roots of its diagonal

see that the matrix of normal equations, N, can be immediately used as the

-1

will Ъе uncorrelated if L is uncorrelated, i.e. P is diagonal, and if the design matrix A is orthogonal. On the other hand, N may he diagonal even for some other general matrices P, A.

Let us now turn once more hack to the "adjustment" of the sample mean (see 6.4.3). It is left to the student to show that the normal equations degenerate into a single- equation, namely equation (6.40) On the other hand, using eq. (6.91), we obtain the estimated variance of the mean x as

^лгп ^{л л}ф ^л

^А р V PV V PV / , \

2

Evidently the estimated variance of x differs from the variance

(see eq. б.бо) in the denominator. By analogy we define a new statis-

"2

tical quantity, the estimated variance S of a sample L

л p 1 — P 1

SL = —-—E (£.-£)=——- T) n - 1 . , 1 n - 1 .

n n _{A p}

E v. i=l " i=l

(6.93)

(compare with eq. 3.6) which is used in statistics wherever the mean I of the sample L is also being determined. It is again left to the student to show that using the estimated variances for the grouped observations (see 6Л.2) the formula(6.92) (instead of 6.60) can be derived using the argument at ion of 6.4.2 and 6.4.3.

The estimated variances of the sample L and its mean £ can be

also computed using non-normalized weights,.i.e. weights p^ for which

n

£ p. ф 1 (see 6.4.6). It can be shown that the appropriate formulae are i«l ¹

: 2 1 ? - 2

and

^sl ⁼7-—^ A ^pi ^vi ' ⁽⁶-⁹⁵⁾

(n-1) _E p 1=1 i=l

To conclude this section, let us try to interpret the meaning of the variance factor к, introduced for the first time in б. U • 5 • Let us take, for simplicity, an experiment yielding a unit matrix of normal equations, i.e. N = I. What would he the variance-covariance matrix of the solution vector X? It will he a diagonal matrix

= diag (к", k,*..₅k). (6.96)

2 ^л

This implies that all the variances Sa of the components of X equal to

x. 1

к. Since the square roots of the diagonal elements of N (all equal to l) can be considered as the weights P^ of the components x^ of X we can also

write:

P, S ² = P₀S₀² = . . . = P S ² = к . (6.97)

1 1 2 2 n n

Comparison with equation (6.59) gives some insight into the role the