
- •Introduction to adjustment calculus
- •Introduction to adjustment calculus (Third Corrected Edition)
- •Introduction
- •2. Fundamentals of the mathematical theory of probability
- •If d'cd; then p (d1) £ lf
- •Is called the mean (average) of the actual sample. We can show that m equals also to:
- •3.1.4 Variance of a Sample
- •Is called the variance (dispersion) the actual sample. The square root 2
- •In the interval [6,10] is nine. This number
- •VVII?I 0-0878'
- •In this case, the new histogram of the sample £ is shown in Figure 3.5.
- •Is usually called the r-th moment of the pdf (random variable); more precisely; the r-th moment of the pdf about zero. On the other hand, the r-th central moment of the pdf is given by:
- •3.2.4 Basic Postulate (Hypothesis) of Statistics, Testing
- •3.3.4 Covariance and Variance-Covariance Matrix
- •X and X of a multivariate X as
- •It is not difficult to see that the variance-covariance matrix can also be written in terms of the mathematical expectation as follows:
- •3.3.6 Mean and Variance-Covariance Matrix of a Multisample The mean of a multisample (3.48) is defined as
- •4.2 Random (Accidental) Errors
- •It should be noted that the term иrandom error" is used rather freely in practice.
- •In order to be able to use the tables of the standard normal
- •X, we first have to standardize X, I.E. To transform X to t using
- •Is a normally distributed random
- •4.10 Other Measures of Dispersion
- •The average or mean error a of the sample l is defined as
- •5. Least-squares principle
- •5.2 The Sample Mean as "The Maximum Probability Estimator"
- •5.4 Least-Sqaures Principle for Random Multivariate
- •In very much the same way as we postulated
- •The relationship between e and e for a mathematical model
- •6.4.4 Variance Covariance Matrix of the Mean of a Multisample
- •Itself and can be interpreted as a measure of confidence we have in the correctness of the mean £. Evidently, our confidence increases with the number of observations.
- •6.4.6 Parametric Adjustment
- •In this section, we are going to deal with the adjustment of the linear model (6.67), I.E.
- •It can be easily linearized by Taylor's series expansion, I.E.
- •In which we neglect the higher order terms. Putting ax for X-X , al for
- •The system of normal equations (6.76) has a solution X
- •In sections 6.4.2 and 6.4.3. In this case, the observation equations will be
- •In matrix form we can write
- •In metres.
- •6.4.7 Variance-Covariance Matrix of the Parametric Adjustment Solution Vector, Variance Factor and Weight Coefficient Matrix
- •I.E. We know the relative variances and covariances of the observations only. This means that we have to work with the weight matrix к£- 1
- •If we develop the quadratic form V pv 3) considering the observations l to be influenced by random errors only, we get an estimate к for the assumed factor к given by
- •Variance factor к plays. It can be regarded as the variance of unit
- •In metres,
- •Is satisfied. This can be verified by writing
- •Into a . О
- •6.U.10 Conditional Adjustment
- •In this section we are going to deal with the adjustment of the linear model (6.68), I.E.
- •For the adjustment, the above model is reformulated as:
- •Is not as straightforward, as it is in the parametric case (section 6.4.6)
- •VeRn VeRn
- •Into the above vector we get 0.0
- •0.0 In metres .
- •In metres.
- •Areas under the standard normal curve from 0 to t
- •Van der Waerden, b.L., 1969: Mathematical Statistics, Springer-Verlag.
5. Least-squares principle
5.1 The Sample Mean as "The Least Squares Estimator"
One may now ask oneself a hypothetical question: given the sample L = (, i = 1, 2, . .. , n, what is the value £° that makes the summation of the squares of the discrepancies
Vi = £i " £° 5 1 = 1э 2э * * * ' Пэ (5-1)
the smallest (i.e. minimum)?
The above question may he stated more precisely as follows: Defining a "new variance" S*2 as
S*2 = - Z U.-£°)2=~ Z v2 , (5-2)
n i==1 i n 1=1 1
find the value £° that is going to give us the smallest (minimum)
2
value of S* .
Obviously, such a question can be answered mathemat i с ally. From equation (5-2), we notice that S*2 is a function of £°, which is the only free variable here, and can be written as
S*2 = S*2U°) . (5-3)
We know that:
3S*2
min [S* (£°) ] implies that = 0 .
£°eR Э£°
Hence, by differentiating equation (5-2) with respect to 1° and equa*-ting it to zero, we get:
n i=1 L3£o x
= — E [2(4.-A°)(-l)] =~ U.-4°) = 0 , n i=1 l n 1=1 l '
that is:
E (1.-1°) = 0
i=l i
The above equation can be rewritten as:
n n
I £. = 2 1° = n£° , i=l 1 i=l
which yields
1° = ^ ? 4. = I (5-4)
П 1=1 1
The result (5-4) is nothing else hut the "sample mean" 1 again. In other words, the mean of the sample is the value that minimizes the sum of the squares of the discrepancies making them equal to the residuals, (see section 4.8).
This is the reason why the mean I is sometimes called the least-squares estimation (estimator) of &\ i.e. of ; the name being derived from the process of minimization of the squares of the discrepancies . We also notice that I minimizes the variance of the sample if we want to regard the variance as a function of the mean.
Note that the above property of the mean is completely independent of the PDF of the sample. This means that the sample mean I is , always "the minimum variance estimator of £" whatever the PDF may be.
5.2 The Sample Mean as "The Maximum Probability Estimator"
Let us take our sample L again, and let us postulate an underlying
parent PDF to be normal (see section U.5) with a mean y^ = £° and a
2 .
variance an given by:
£ to ° n n ^
(5.5)
a 2 = s*2 = i- A (£„ - £°)2 = ^ A Vi • £ n 1=1 i n i=l
We say that the normal PDF, N(y^, a£; £) = N(£°, S*; £) is the most
probable underlying PDF for our sample L (L = (£^), i = 1, 2, ... n)
if the combined probability of simultaneous occurrence of n elements?
tkat have the normal distribution N(£°, S*; £)* at the same places as L is
maximum. In other words, we ask that:
P[(£i < £ < Si + 5£ ), i = 1, 2. . n] =
n
П N(£°, S*; £. ) . 6£. (5-6)
i=l 1 1
be maximum with respect to the existing free parameters. By examining equation (5*6), we find that the only free parameter is £° (note that S* is a function of £°), and hence we can write the above combined probability as a function of £° as follows:
P[(£. <£<£.+ 6£.), i = 1, 2, . . n] = X (£°) (5,7) 1 - 1 1
Note that 6£'s are some values depending on L and therefore are determined uniquely by L.
We shall show that the value of £° satisfying the above condition is (for the postulated normal PDF) again the value rendering the smallest value of S*. We can write:
n
max [XU°)J = max [ П N(£°, S*; «,.) 6£.] £°eR £°eR i=l 1 1
n n (£. -£°)
= max-. [ П -— П exp ( - ) 5£. ]
£°eR i=l S*/(2tt) i=l 2S* X
n „ n (£,-£°)2
= max
о
[( _^_)* П exp ( - —6£ 1 , (5.8;
n
Here П 81. is determined Ъу L, and hence does not lend itself to maximiza-i=l 1
tion. It thus can he regarded as a constant, i.e.
1 n (l.-l°)2
max [X(£0)] =max [ (—±— )n n exp (- —) j . (5.9) £o£R £0eR sm21t) i=l 2S*
Let us denote the second term in- the RHS of equation (5*9) by Q, which can he expressed as:
n U.-£°)2
Q = П exp (-x ), where x = —5— (5-10)
1—± 1 1 2S* '
This implies that:
n n
in Q = to ( П exp (-x.)) == E £n (exp(-x. )) ,
i=l 1 i=l 1
or
n
Q = exp (E (-x )) . (5.11)
i=l 1
From equations (5-9) э (5-Ю) and (5-11) we get:
n (A -SL°)2 n
П exp (- ) = exp [- ^— I U.-£°r] .
i=l 2S* 2S* i=l
The condition (5-9) can be then rewritten as:
(5-12)
2S*2
i=l
'
1
max [АЦ0)] = max [( i ) exp (- E (I .-H°)2)],( 5-13)
£ eE S*/(2tt)
From equation (5-5)» we have:
n о ? ?
E (£ -A ) = nS* .
i=l
Hence by substituting this value into equation (5-13) we get:
1 П
max )] = max [ ( ) exp(- —) ].
£°eR A°eR S*/(2tt) d
(5-lU)
Since the only quantity in equation (5-1*0 that depends on SL° is S*, we can write:
n
А°еЯ
max UU°)] = max [ (—) ] = max [(S*)~n] £°e'R S*
= min [(S*)n ]. A°eR
(5-15)
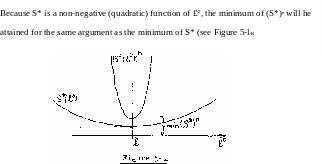
Finally, our original condition (equation (5-9) can be restated as:
max [XU°)] = min [S*U°)] = min [S*2(l°)] (5-l6)
£°eR £°eR £°eR
which implies that
3S* _ 9S*2 _
that is:
n
— T- v2 = 0 . (5-17)
9£° i=l 1
Obviously, the condition (5-17) is the same condition as that of the "minimum variance" discussed in the previous section, and again we have
£° = I .
We have thus shown that under the postulate for the underlying PDF, the mean 1 of the sample L is the maximum probability estimator for £. As a matter of fact, we would find that the requirement of maximum probability leads to the condition
3S*
0 (5.18)
Э£°
for quite a large family of PDF1s, in particular the symmetrical PDF1s» If one assumes the additional properties of the random sample as mentioned in 3.2.4. then additional features of the sample mean can be shown. This again is considered beyond the scope of this course.
5.3 Least-Squares Principle We have shown that the sample mean renders always the minimum sum of squares of discrepancies and that this property is required, for a lar^e family of postulated PDF1 s, to yield the maximum probability for the underlying
PDF. Hence the sample mean £, which automatically satisfies the condition of the least sum of squares of discrepancies, is at the same time the most probable value of the mean у of the underlying PDF under the con-dition that the underlying PDF is symmetrical. This is the necessary and sufficient condition for the sample mean to be both the least squares and the maximum probability estimator, i.e. for both estimators to be equivalent.
The whole development we have gone through does not say anything about the most probable value of the standard deviation a of the underlying PDF*). a^ has to be postulated according to equation (4.23).
The idea of minimizing the sum of squares of the discrepancies is known as the least-squares principle,and has got a fundamental importance in the adjustment calculus. We shall show later how the same principle is used for all kinds of estimates (not only the mean of a sample) and how it is developed into the least-squares method. However, the basic limitations of the least-squares principle should be born in mind, namely
*) Some properties of the standard deviation S can be revealed if the additional properties of the random sample are assumed (see 3.2.4).
(i) A normal PDF (or some other symmetrical PDF) is postulated, (ii) The least-squares principle does not tell anything about the best estimator of a^ with respect to the mean y^ of the postulated PDF.
