Clx.Ru - реклама в интернет

 

4) . Докажите это в качестве упражнения, сделав замену и применив предыдущую табличную формулу.

5) . Для доказательства воспользуемся формулой . Далее, имеем:

 

 

 

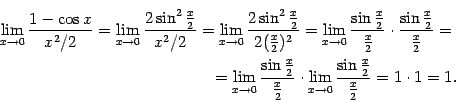
Это означает, что доказываемая эквивалентность имеет место.

6) . Для доказательства этой эквивалентности сделаем такое преобразование:

 

 

 

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

 

 

и мы доказали формулу 6.

В частном случае, при , получаем эквивалентность

) .

7) ( ). Для доказательства сделаем замену и выразим через : . Согласно формуле 6, при , откуда . Из непрерывности логарифма следует, что и, значит, при . В этой формуле осталось лишь сменить обозначение переменного на , чтобы получить формулу 7.

В частном случае, при , получаем эквивалентность

) .

Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней .

1)	.
2)	.
3)	.
4)	.
5)	.
6)	( ).
)	.
7)	( ).
)	.

CLX.ru - реклама в интернет

Приведём примеры применения табличных формул для раскрытия неопределённостей вида .

 

 

        Пример 2.37Вычислим предел . Для этого в числителе вынесем за скобку , а к знаменателю применим формулу 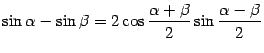, где , . Получим

Мы заменили на эквивалентную величину (учтя при этом, что при ), на эквивалентную величину (учтя, что при ), затем сократили числитель и знаменатель на и, наконец, воспользовались тем, что функции и непрерывны и что и .

 

 

 

        Пример 2.38Вычислим предел

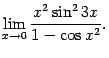
Заменим в числителе на эквивалентную величину , а знаменатель -- на эквивалентную величину . После этого можно будет сократить дробь на и получить ответ:

    

 

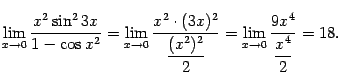
Ещё раз обратим внимание читателя, что все формулы таблицы эквивалентных бесконечно малых относятся к базе . Следовательно, те же эквивалентности имеют место и при односторонних базах и . Если же рассматриваемый пример содержит неопределённость вида при какой-либо другой базе, то часто предел можно свести к пределу при "стандартной" базе (или , или ) с помощью подходящей замены переменной, а затем воспользоваться табличными эквивалентностями.

 

 

        Пример 2.39Вычислим предел .

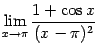Если сделать замену , то при новая переменная будет, очевидно, стремиться к 0, то есть база перейдёт при такой замене в "стандартную" базу . Подставляя и учитывая формулу приведения для косинуса, получаем:

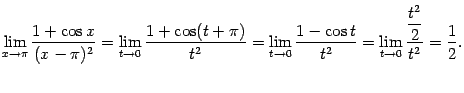
Мы применили табличную формулу 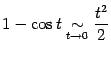, а затем сократили дробь на и получили ответ.

 

Применяя формулы таблицы эквивалентностей бесконечно малых последовательно, мы можем получать (и использовать для вычисления пределов) цепочки эквивалентностей произвольной длины.

 

 

        Пример 2.40Можно, например, получить следующую формулу:

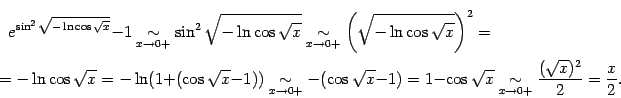
Здесь мы последовательно воспользовались формулами

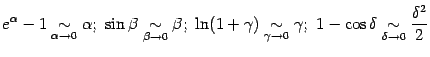
и учли, что величины , , , являются бесконечно малыми при .

Используя полученную в результате эквивалентность

мы можем, например, вычислить предел

Упражнения на вычисление пределов

Упражнение 2.9Вычислите предел:

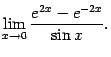
Ответ: 4.

Упражнение 2.10Вычислите предел:

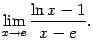
Ответ: .

Упражнение 2.11Вычислите предел:

Ответ: 1.

Упражнение 2.12Вычислите предел:

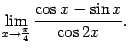
Ответ: .

CLX.ru - реклама в интернет

Упражнение 2.13Вычислите предел:

Ответ: 2.

Упражнение 2.14Вычислите предел:

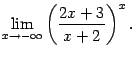
Ответ: 0.

Упражнение 2.15Вычислите предел:

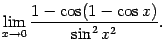
Ответ: .

Упражнение 2.16Вычислите предел:

Ответ: .

Упражнение 2.17Вычислите предел:

Ответ: .

Упражнение 2.18Вычислите предел:

Ответ: 1.
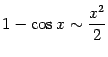