Clx.Ru - реклама в интернет

или таков:

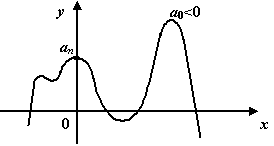
Рис.1.16.График многочлена чётной степени при

а при нечётном значении степени -- таков:

Рис.1.17.График многочлена нечётной степени при

или таков:

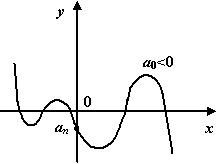
Рис.1.18.График многочлена нечётной степени при

5. Показательная функция (экспонента).Это функция вида (, ). Для неё , , , и при график имеет такой вид:

Рис.1.19.График показательной функции при

При вид графика такой:

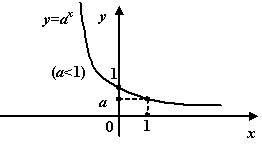
Рис.1.20.График показательной функции при

Число называетсяоснованиемпоказательной функции.

6. Логарифмическая функция.Это функция вида (, ). Для неё , , , и при график имеет такой вид:

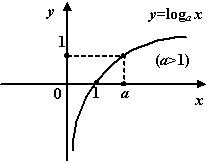
Рис.1.21.График логарифмической функции при

При график получается такой:

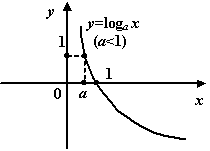
Рис.1.22.График логарифмической функции при

Число называетсяоснованиемлогарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия.

7. Функция синус: . Для неё ; функция периодична с периодом и нечётна. Её график таков:

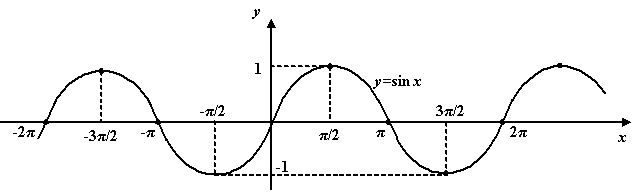
Рис.1.23.График функции

8. Функция косинус: . Эта функция связана с синусом формулой приведения: ; ; период функции равен ; функция чётна. Её график таков:

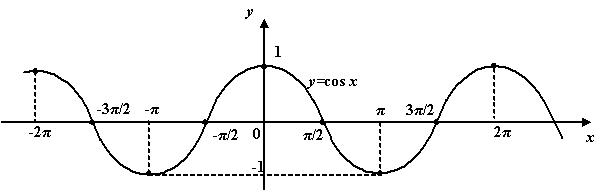
Рис.1.24.График функции

9. Функция тангенс: (в англоязычной литературе обозначается также ). По определению, 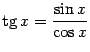. Функция нечётна и периодична с периодом ;

 

 

то есть не может принимать значений , , при которых (стоящий в знаменателе) обращается в ноль.

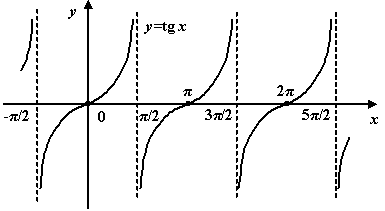
Рис.1.25.График функции

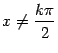10. Функция котангенс: (в англоязычной литературе также ). По определению, . Если ( ), то 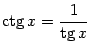. Функция нечётна и периодична с периодом ;

 

 

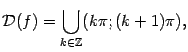
то есть не может принимать значения вида , , при которых обращается в 0.

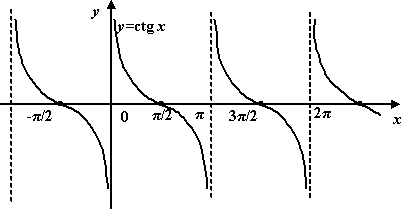
Рис.1.26.График функции

11. Абсолютная величина (модуль): , . Эта функция определяет расстояние на вещественной оси от точки до точки0:

 

 

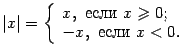
Функция чётная, её график такой:

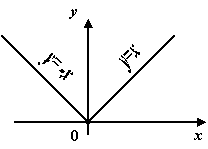
Рис.1.27.График функции

12. Обратные тригонометрические функции.Это функции арксинус, арккосинус, арктангенс и арккотангенс. Они определяются как функции, обратные кглавным ветвямсинуса, косинуса, тангенса и котангенса соответственно, о чём подробнее в конце главы, в разделе Обратная функция.

13. Расстояние до начала координат на плоскости и в пространстве.На координатной плоскости расстояние от точки до точки определяется по формуле (по теореме Пифагора) и, следовательно, задаёт функцию

 

 

Эта функция имеет область значений

 

 

График её ограничения на круг построен впримере 1.8.

Аналогично, расстояние в пространстве от точки до точки определяется по формуле и задаёт функцию

 

 

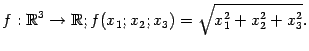
Эта функция имеет ту же область значений

 

 

что и в двумерном случае.

14. Арифметическая прогрессия.Функция , задаваемая формулой

 

 

где , -- фиксированные числа, а , называетсяарифметической прогрессией. Число называется при этомпервым членом прогрессии, а число --разностью прогрессии. Функцию можно представить как ограничение на множество натуральных чисел линейной функции с угловым коэффициентом и свободным членом . Арифметическую прогрессию можно задать и другим,рекуррентнымспособом:

 

при

 

Уравнение, рекуррентно задающее арифметическую прогрессию, -- это линейное уравнение в конечных разностях первого порядка, с одним начальным условием .

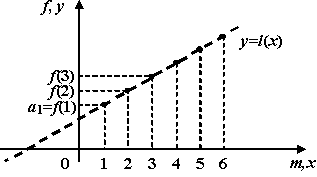
Рис.1.28.График арифметической прогрессии

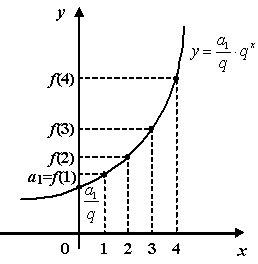
15. Геометрическая прогрессия.Функция , задаваемая формулой

 

 

где , -- фиксированные числа, а , называетсягеометрической прогрессией. Число называется при этомпервым членом прогрессии, а число --знаменателем прогрессии. Функцию (при , ) можно представить как ограничение на множество натуральных чисел показательной функции с основанием , умноженной на постоянный коэффициент , то есть функции

 

 

Рис.1.29.График геометрической прогрессии

Геометрическую прогрессию можно задать и иначе, рекуррентным способом:

 

при

Третий способ задания функции: указание процедуры вычисления

Во многих случаях функцию приходится задавать сложным образом, так как предыдущие способы задания функций не годятся. Приведём такой пример.

 

 

        Пример 1.17Пусть и -- это наибольший корень уравнения . Этим условием задаётся некоторая функция . Её область определения не пуста, так как, например, при получается уравнение , у которого имеется единственный корень , так что и, следовательно, . Однако ни выразить значение формулой или иным "конечным" образом, ни полностью описать область определения функции не удаётся. В этом случае, однако, для задания функции возможноуказание некоторой процедурывычисления её значений , которую можно реализовать в видекомпьютерной программы. Эта процедура станет по каждому конкретно заданному значению определять значение либо указывать, что исходное уравнение не имеет корней, то есть что не принадлежит .

CLX.ru - реклама в интернет

Изменяя число в некотором диапазоне, можно найти соответствующие значения с заданной наперёд точностью и, например, построить график по точкам.

 

Описанный в предыдущем примере способ задания функции, то есть реализация вычисления значений функции в виде компьютерной процедуры, приобретает всё большее значение по мере развития вычислительной техники и расширения области её применения.

Если числовая функция , где , реализуется в виде компьютерной процедуры, то строить график этой функции проще всего по точкам, то есть перебирая с некоторым шагом точки , , и нанося на координатную плоскость точки вида и, быть может, для наглядности соединяя отрезками пары соседних точек. Этот способ, несмотря на свою подозрительную простоту, -- вполне возможный (а может быть, и единственно реальный) способ построения графика при отсутствии какой-либо удобной формулы, выражающей значения через .

Следует иметь в виду, что процедура, выдающая значения функции по заданным , делает это, как правило, лишь приближённо, да и сами значения аргумента часто также оказываются заданными приближённо. Если точность вычислений в какой-либо задаче очень важна, то следует проделать анализ возможной погрешности в значении , вызванной тремя причинами:

а) приближённостью задания переменного (погрешностью аргумента);

б) приближённостью способа получения значения (погрешностью метода);

в) приближённостью выполнения арифметических действий при вычислениях по программе, реализующей метод на компьютере (погрешностью вычислений).

Тщательный анализ погрешности обычно бывает провести гораздо сложнее, чем разработать сам алгоритм вычисления . Если же такой анализ не проводится, то о точности произведённых вычислений судят по косвенным признакам: "хорошо ли ведёт себя" полученный график , согласуется ли он с интуитивными представлениями о том, как выглядит процесс, описываемый функцией , и по другим косвенным признакам.

Композиция функций

Если даны два отображения и , где , то имеет смысл "сквозное отображение" из в , заданное формулой , , которое называетсякомпозициейфункций и и обозначается .

Рис.1.30.Сквозное отображение из в

Таким образом, , при всех . Другое название композиции--сложная функция(так как сквозное отображение "сложено" из отображений и ).

Пример 1.18Пусть , , и , . Тогда , и определена композиция

CLX.ru - реклама в интернет

Упражнение 1.3Покажите, что если заменить множество в предыдущем примере на , то композиция снова будет определена, но равна теперь , а не .

Пример 1.19Пусть , , и , . Тогда определена композиция , заданная формулой . По известной формуле приведения полученная композиция-- это косинус: при всех .

Замечание 1.5Даже если для функций и имеют смысл обе композиции и (что бывает далеко не для любой пары функций и ), то функции и не обязаны совпадать; как правило, это не так.

Пример 1.20Пусть и , . Тогда , а . Очевидно, что это разные функции: при всех , а принимает значение , например, при .

Применяя композицию функций, которые сами могут получаться как композиции, мы можем получать сложные функции вида и более длинные композиции.

Основные обозначения и определения Обратная функция

Рассмотрим теперь поподробнее понятие обратной функции, введённое в начале главы.

Если -- взаимно-однозначное отображение (биекция), то для любого однозначно определен такой элемент , что . Тем самым однозначно определено соответствие , называемоеобратной функциейпо отношению к функции . Обратная функция для обозначается . Таким образом,

Очевидно, что согласно определению мы имеем тождество , то есть композиция -- этотождественное отображение , для любого . Точно так же , то есть , , , если .

Последнее утверждение означает, что функция, обратная к , равна : , то есть что функции и -- это двевзаимно обратныефункции.

Пример 1.21Если -- ограничение функции на отрезок (это ограничение называетсяглавной ветвью синуса), то отображение -- биекция.

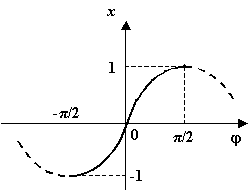
Рис.1.31.Главная ветвь синусаCLX.ru - реклама в интернет

Поэтому существует обратная функция , называемаяарксинусоми обозначаемая или (второе обозначение употребляется в англоязычной математической и инженерной литературе). Таким образом,

еслии

Пример 1.22Аналогично определяется функцияарккосинус(обозначается или ). Это функция, обратная к ограничению функции на отрезок (такое ограничение называетсяглавной ветвью косинуса):

еслии

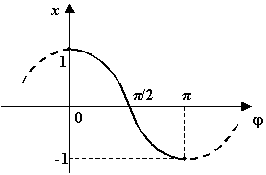
Рис.1.32.Главная ветвь косинусаCLX.ru - реклама в интернет

Пример 1.23Функцияарктангенс(обозначается , или , или )-- это функция, обратная к ограничению функции на интервал , то есть обратная кглавной ветви тангенса:

Так как -- это биекция, то обратная функция определена при всех :

еслии

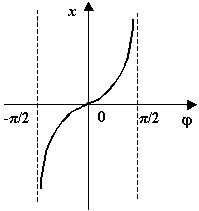
Рис.1.33.Главная ветвь тангенса

Упражнение 1.4Дайте определение функции арккотангенс (обозначается ), рассмотревглавную ветвь котангенса-- ограничение функции на интервал .

Упражнение 1.5Вспомните или выведите простые соотношения, которым удовлетворяют значения функций:

а) и ;

б) и .

График обратной функции получается из графика исходной функции , если у каждой точки графика поменять местами координаты и :

так как состоит из таких точек , что , а -- из таких точек , что ; но, согласно определению обратной функции, равенства и эквивалентны.

В случае, когда , , перестановка координат геометрически может быть описана как преобразование симметрии относительно прямой , то есть относительно биссектрисы первого и третьего координатных углов.

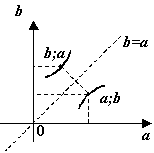
Рис.1.34.Симметричные точки графиков функций и

Значит (в случае , ), графики и симметричны относительно этой биссектрисы, если ось, по которой откладываются значения аргумента функции, каждый раз размещать горизонтально.

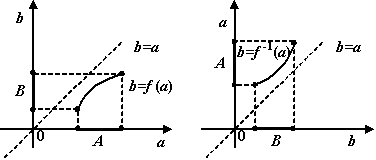
Рис.1.35.Графики взаимно обратных функций расположены симметрично

Пример 1.24Согласно с последним замечанием, мы легко построим теперь графики обратных тригонометрических функций и :

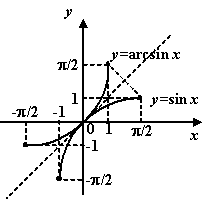
Рис.1.36.Графики главной ветви и

Рис.1.37.Графики главной ветви и

Рис.1.38.Графики главной ветви и

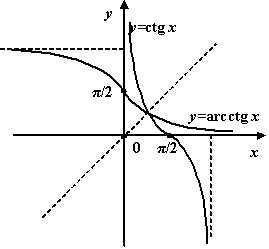
Рис.1.39.Графики главной ветви и