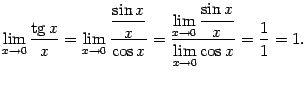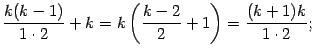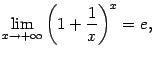Clx.Ru - реклама в интернет

При неравенство (2.2) означает, что ; так как 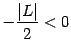, то и при всех и, опять-таки, функция определена во всех точках окончания ; она удовлетворяет неравенству

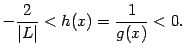
В любом случае получаем, что функция определена во всех точках и при этих удовлетворяет неравенству 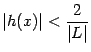, что означает локальную ограниченность функции при базе .

На основе этой леммы мы докажем обещанное выше утверждение о пределе отношения.

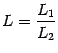Теорема 2.10Пусть при одной и той же базе существуют пределы и , причём . Тогда функция определена на некотором окончании базы , существует предел , и , то есть предел отношения равен отношению пределов числителя и знаменателя.

Доказательство. Представим отношение в виде 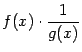, в котором и первый, и второй множители определены на некотором окончании базы (относительно второго множителя см.предыдущую лемму). Поэтому и исходное отношение имеет смысл при всех .

Утверждение о том, что 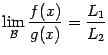, эквивалентно тому, что разность 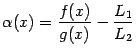-- бесконечно малая величина. Приводя эту разность к общему знаменателю, получим, что 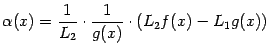. Величина -- постоянная и, следовательно (см.пример 2.11), локально ограничена; функция -- тоже локально ограничена при базе (по предыдущей лемме). Значит, с учётом предложения 2.1 и теоремы 2.7, будет доказано, что величина бесконечно малая, если мы покажем, что бесконечно мала при базе величина . Найдём предел этой величины. По свойству линейности предела ( следствие 2.5)

Это означает, что величина бесконечно мала.

Замечание 2.5Как и в случае пределов суммы и произведения, можно сделать замечание (аналогичное замечаниям 2.2 и 2.3): если существует предел отношения, то пределы числителя и знаменателя, вообще говоря, существовать не обязаны. Приведите сами пример, иллюстрирующий это утверждение.

Пример 2.16Найдём предел

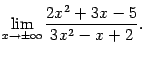
Разделим числитель и знаменатель дроби на старшую степень , то есть на , и получим предел

В этом пределе знаменатель стремится к 3, так как и (здесь мы применили теорему о пределе произведения для последнего слагаемого) и, следовательно, (здесь мы воспользовались линейностью предела). Поскольку предел знаменателя оказался не равен 0, то можно применить теорему о пределе отношения и получить, что

Предел числителя, равный 2, мы нашли аналогично пределу знаменателя, пользуясь линейностью предела.

Итак,

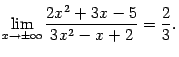
Заметим, что предел отношения многочленов оказался равен отношению коэффициентов при старшей степени , то есть, в данном случае, при .

Аналогично решаются и другие примеры на вычисление пределов отношения двух многочленов при , а также пределов отношения некоторых других функций, например, связанных с корнями из многочленов.

Пример 2.17Найдём предел

Для этого поделим числитель и знаменатель дроби на (под знаком корня в знаменателе для этого придётся поделить на ):

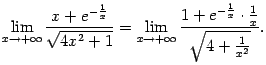
Поскольку , то подкоренное выражение стремится к 4, а весь знаменатель-- к . Предел знаменателя оказался отличен от 0, поэтому предел отношения равен отношению пределов. Найдём предел числителя. Поскольку при всех (так как показатель степени отрицателен), то величина локально ограничена при базе и поскольку величина -- бесконечно малая при этой базе, то произведение также бесконечно мало, то есть стремится к 0 при . Значит, предел числителя равен

а исходный предел--

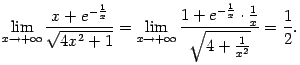
Упражнение 2.5Найдите пределы:

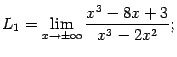
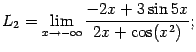
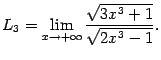
Ответ: ; ; .

Указания:поделите числитель и знаменатель дроби в первом примере на , во втором-- на и в третьем-- на . Во втором примере воспользуйтесь тем, что и -- величины, ограниченные при всех (и, следовательно, локально ограниченные при любой базе).

Теорема 2.11(теорема "о двух милиционерах")Пусть даны три функции , и , при всех из некоторого окончания базы связанные неравенством

Пусть функции и имеют общий предел при базе :

Тогда функция также имеет предел при базе , равный тому же числу :

Доказательство. Согласно определению предела, для любого найдутся такие окончания базы и , что при выполняется неравенство

а при -- неравенство

Значит, для окончания при всех выполняются неравенства

то есть

Это означает, что предел величины равен .

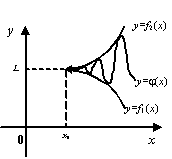
Рис.2.21.Два милиционера и и пьяный движутся в участок

(Происхождение названия теоремы таково: пусть график функции -- это траектория движения первого милиционера в участок, график -- второго милиционера туда же, а график -- траектория движения нетрезвого гражданина, находящегося, в соответствии с неравенством

в любой момент между двумя милиционерами. Тогда и этот гражданин неизбежно придёт туда же, в участок .)

Теорема 2.12(теорема о пределе неотрицательной величины)Пусть при всех из некоторого окончания базы и существует . Тогда . Иными словами, при переходе к пределу знак нестрогого неравенства сохраняется.

Доказательство. Если бы предел был отрицательным, то можно было бы взять и найти такое окончание базы , что при выполняется неравенство , откуда . Это же будет выполнено на некотором окончании , что противоречит предположению, что при всех . Противоречие доказывает, что отрицательным предел быть не может, то есть .

Следствие 2.6Пусть при всех из некоторого окончания базы и существует . Тогда .

Доказательство. Для доказательства достаточно взять функцию , применить к ней доказанную только что теорему и воспользоваться тем, что знак минус можно вынести за знак предела (по свойству линейности предела).

Следствие 2.7(переход к пределу в нестрогом неравенстве)Пусть при всех из некоторого окончания базы выполняется неравенство . Предположим, что существуют пределы и . Тогда (то есть значения пределов связаны тем же нестрогим неравенством, что и функции). То же верно для нестрогого неравенства .

Доказательство. Рассмотрим функцию . По условию теоремы, , причём

Применим к функции теорему о пределе неотрицательной величины и получим, что , то есть , что и требовалось доказать. Для другого нестрогого неравенства доказательство аналогично.

Замечание 2.6Аналогичные утверждения для строгих неравенств (и )неверны. Для того, чтобы в этом убедиться, достаточно рассмотреть предел . Очевидно, он равен 0, хотя при любом из любого окончания базы величина строго положительна.

Рис.2.22.Предел строго положительной величины может оказаться равным 0

Напомним, что функция называетсяне убывающейна множестве , если для любых , таких что , выполняется неравенство , иневозрастающейна , если при и выполняется неравенство .

Теорема 2.13(о пределе монотонной функции)Пусть рассматривается одна из баз , , , которую обозначим . Пусть функция не убывает на некотором окончании базы и ограничена сверху на этом окончании, то есть существует такая постоянная , что при всех . Тогда существует предел , причём .

Рис.2.23.Предел неубывающей ограниченной сверху функции

Доказательствоэтой теоремы достаточно сложно; оно основывается на довольно тонких свойствах системы вещественных чисел, а именно, на том, что у ограниченного снизу множества чисел , где числа ограничивают функцию сверху, существует точная нижняя грань ; она-то и будет пределом неубывающей функции.

Мы ограничимся здесь этим замечанием и поясняющим рисунком, а за подробным доказательством отошлём читателя к полному курсу математического анализа, например, книгам: Г.М.Фихтенгольц,Курс дифференциального и интегрального исчисления, т.1илиС.М.Никольский,Курс математического анализа, т.1.

Имеют место также утверждения, получающиеся из теоремы о пределе монотонной функции сменой знака функции или заменой координаты :

Следствие 2.8Пусть рассматривается одна из баз , , , которую обозначим . Пусть функция не возрастает на некотором окончании базы и ограничена снизу на этом окончании, то есть существует такая постоянная, что при всех . Тогда существует предел , причём .

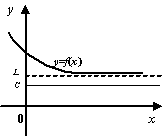
Рис.2.24.Предел невозрастающей ограниченной снизу функции

Следствие 2.9Пусть рассматривается одна из баз , , которую обозначим . Пусть функция не убывает на некотором окончании базы и ограничена снизу на этом окончании, то есть существует такая постоянная , что при всех . Тогда существует предел , причём .

Рис.2.25.Предел неубывающей ограниченной снизу функции

Следствие 2.10Пусть рассматривается одна из баз , , которую обозначим . Пусть функция не возрастает на некотором окончании базы и ограничена сверху на этом окончании, то есть существует такая постоянная, что при всех . Тогда существует предел , причём .

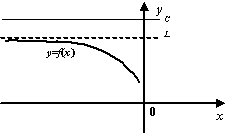
Рис.2.26.Предел невозрастающей ограниченной сверху функции

Первый и второй замечательные пределы

        Определение 2.11Первым замечательным пределом называется предел

    

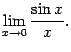
        Теорема 2.14Первый замечательный предел равен

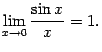
        Доказательство.     Рассмотрим два односторонних предела и и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел также будет равняться 1.

Итак, пусть (этот интервал -- одно из окончаний базы ). В тригонометрическом круге (радиуса ) с центром построим центральный угол, равный , и проведём вертикальную касательную в точке пересечения горизонтальной оси с окружностью (). Обозначим точку пересечения луча с углом наклона с окружностью буквой , а с вертикальной касательной -- буквой ; через обозначим проекцию точки на горизонтальную ось.

Рис.2.27.Тригонометрический кругCLX.ru - реклама в интернет

Пусть -- площадь треугольника , -- площадь кругового сектора , а -- площадь треугольника . Тогда очевидно следующее неравенство:

Заметим, что горизонтальная координата точки равна , а вертикальная -- (это высота треугольника ), так что 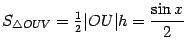. Площадь центрального сектора круга радиуса с центральным углом равна , так что . Из треугольника находим, что . Поэтому 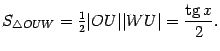Неравенство, связывающее площади трёх фигур, можно теперь записать в виде

Все три части этого неравенства положительны, поэтому его можно записать так:

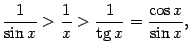
или (умножив на ) так:

Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при предел в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части также будет равен 1.

Итак, осталось доказать, что . Сперва заметим, что , так как равняется длине дуги окружности , которая, очевидно, длиннее хорды . Применяя теорему "о двух милиционерах" к неравенству

при , получаем, что

(2.3)

CLX.ru - реклама в интернет

Простая замена переменной показывает, что и . Теперь заметим, что . Применяя теоремы о линейности предела и о пределе произведения, получаем:

(2.4)

Тем самым показано, что

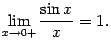
Сделаем теперь замену ; при этом база перейдёт в базу (что означает, что если , то ). Значит,

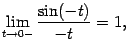
но (-- нечётная функция), и поэтому

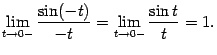
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.     

Доказанная теорема означает, что график функции выглядит так:

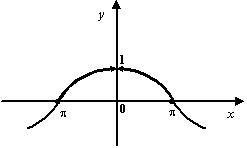
Рис.2.28.График

Приведём примеры применения первого замечательного предела для вычисления других родственных пределов.

        Пример 2.18Вычислим предел .

Очевидно, что

при этом предел знаменателя -- это первый замечательный предел, равный 1 (и, следовательно, не равный 0). Числитель правой части, равный 1, имеет предел 1. Значит, по теореме о пределе отношения,

    

        Пример 2.19Вычислим предел .

Сделаем замену переменного: пусть . Тогда и база переходит в базу . После замены получаем

    

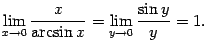
Пример 2.20Вычислим предел .

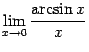Очевидно, что

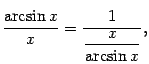
при этом предел знаменателя был вычислен в предыдущем примере; он равен 1. Числитель правой части имеет предел 1. Применяя теорему о пределе отношения, получаем

    

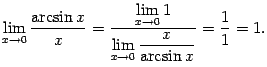
        Пример 2.21Вычислим предел .

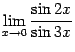Преобразуем функцию под знаком предела следующим образом:

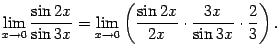
Теперь вынесем постоянный множитель за знак предела и применим теорему о пределе произведения:

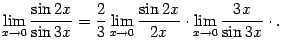
(Чуть ниже мы увидим, что пределы сомножителей существуют, так что применять эту теорему здесь можно.) Заметим, что при заменах и база переходит в базу и , так что

и

Поэтому

    

        Определение 2.12Вторым замечательным пределомназывается предел

    

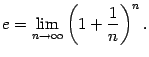
Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называютоснованием натуральных логарифмов.

Теорема 2.15Второй замечательный предел существует. Его значение  -- число, лежащее между и .    

Более подробное изучение числа показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:

Для доказательства теоремы 2.15 нам понадобится следующая лемма; формула, в ней полученная, называется формулой бинома Ньютона.

        Лемма 2.2Пусть и  -- натуральное число. Тогда имеет место формула

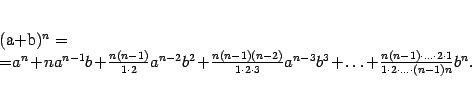
Заметим, что в дроби

очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный , в третьем справа слагаемом -- равный 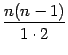, и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.

        Доказательство.     Доказывать утверждение леммы будем по индукции по параметру . При формула 2.2, очевидно, верна:

(Заметим, что при и формула 2.2 также хорошо известна:

и

Предположим, что она верна для , и докажем, что тогда она верна и при . Действительно,

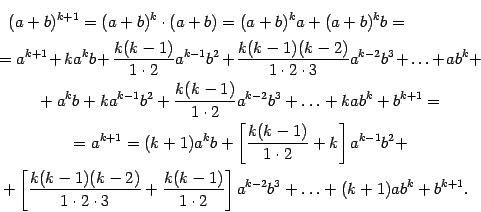
При этом в квадратных скобках получается:

и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при .

        Доказательствотеоремы 2.15.     Рассмотрим последовательность и применим к формулу бинома Ньютона при и . Получим

Покажем, что последовательность ограничена сверху. Для этого заменим все дроби , , ..., на 1. Все эти дроби меньше 1, так что сумма в правой части формулы (Доказательство теоремы 2.15) увеличится:

Далее, заменим все числа в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:

В правой части получилась сумма членов геометрической прогрессии. Она равна

Поэтому

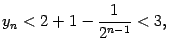
что и означает ограниченность последовательности сверху числом 3.

Покажем теперь, что последовательность не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде

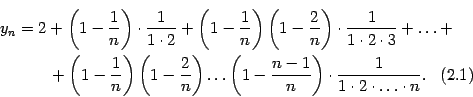
В аналогичной формуле, написанной для вместо , во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое

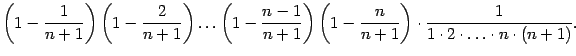
Следовательно, при росте номера члены последовательности строго возрастают: при всех .

Применим теперь к возрастающей ограниченной сверху последовательности теорему о пределе монотонной ограниченной функции ( теорема 2.13) и получим, что существует предел

причём число не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что . Так как все последующие члены ещё больше, то и предел , на основании теоремы о переходе к пределу в неравенстве ( следствие 2.7), не меньше числа , что и завершает доказательство теоремы.

        Замечание 2.7Можно также показать, что

(2.5)

однако строгое доказательство достаточно тяжело, и мы его здесь пропускаем.

В формуле (2.5) можно сделать замену , при этом база перейдёт в базу , и мы получим

    

        Упражнение 2.6Покажите, что имеют место также равенства

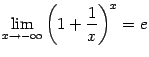
и

На этой основе, применяя теоремы о связи двусторонних пределов с односторонними, покажите, что

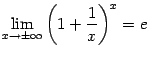
и

    

Формулы в этих замечании и упражнении представляют собою другую форму записи второго замечательного предела. Мы сохраним название второй замечательный пределза всеми этими формулами.

        Пример 2.22Найдём предел .

Здесь параметр -- фиксированное число. При вычислении предела он будет рассматриваться как постоянная. Сделаем замену , тогда и . Поэтому

(Здесь мы воспользовались, пока на интуитивном уровне, тем, что степенная функция непрерывна, то есть что . Более подробно понятие непрерывности функций мы будем изучать ниже, в разделе Использование непрерывности функций при вычислении пределов.) Полученная формула даёт нам возможность выразить экспоненциальную функцию как некоторый предел.

С помощью похожей замены вычисляются пределы функций вида в случае, когда основание степени при некоторой базе стремится к 1, а показатель степени -- к бесконечности (то есть является бесконечно большой функцией при данной базе; о бесконечно больших см. ниже, в разделе Бесконечно большие величины и бесконечные пределы). Такие выражения, а также и связанные с ними пределы, называютсянеопределённостями вида . О неопределённостях других видов пойдёт речь ниже, после примера 2.29.

Обратим внимание читателя, что -- это лишь условная запись: 1 здесь указывает, что основание степенистремитсяк 1 (и вовсе не обязательноравно 1); в "показателе степени" стоит вообще не число, а символ бесконечности. Поэтому было бы грубой ошибкой, встретив такую условную запись (или написав её), сделать вывод о том, что единица, мол, в любой степени даёт единицу, и поэтому ответ равен единице. С условными символами в этой записи нельзя действовать так же, как с числами. Предыдущий пример, в котором основание степени стремится к 1, а показатель степени к , даёт как раз неопределённость вида . Однако значение предела равно , а этот результат может бытьлюбым положительным числом, в зависимости от того, какое значение взято.

Вот ещё один пример на раскрытие неопределённости вида .

Пример 2.23Найдём предел .

Здесь основание степени имеет предел

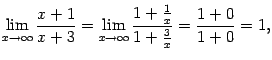
а показатель степени . Поэтому можно применять тот же приём сведения ко второму замечательному пределу, что в предыдущем примере. Для начала найдём, что следует взять за бесконечно малую величину . Поскольку основание степени стремится к 1, то оно равно , где (см.  теорему 2.4). Значит,

Теперь преобразуем функцию, стоящую под знаком предела:

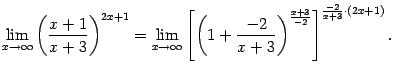
Выражение, стоящее в квадратных скобках, имеет вид и при стремится к числу (это второй замечательный предел), а предел показателя степени мы найдём отдельно:

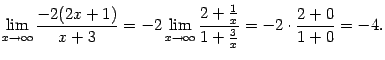
Поэтому

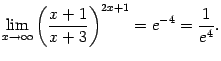
(Мы воспользовались тем, что если и , то . Это следует из непрерывности показательной и логарифмической функций, если учесть, что .)

        Замечание 2.8Не любые пределы величин вида вычисляются с помощью сведения ко второму замечательному пределу. Ещё раз напомним, что так надо поступать лишь в случае, когда основание степени при данной базе стремится к 1, а показатель степени -- к бесконечности. В иных ситуациях можно бывает для вычисления предела обойтись более простыми рассуждениями. Например, при нахождении предела

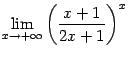
можно заметить, что основание степени стремится к , так что получается формально . Это выражение не является неопределённостью (в отличие от выражения ), так как основание степени при достаточно больших близко к (и заведомо меньше, скажем, ) и при возведении в неограниченно увеличивающуюся степень будет меньше и, следовательно, будет стремиться к 0. Так что

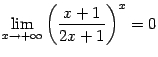
и прибегать к помощи второго замечательного предела не пришлось.     

Бесконечно большие величины и бесконечные пределы

        Определение 2.13Пусть функция определена на некотором окончании базы и имеет следующее свойство:для любого, как угодно большого, положительного числа можно найти такое окончание базы , что при любом будет выполнено неравенство

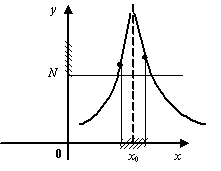
Рис.2.29.Бесконечно большая при базе

Тогда функция называетсябесконечно большойпри базе ; это обозначается так:

или так:

или даже так:

CLX.ru - реклама в интернет

Если при этом при , то дляположительнойбесконечно большой можно писать или , а если , то дляотрицательнойбесконечно большой можно писать или .

Нужно, конечно, чётко осознавать, что предел, равный бесконечности, -- это чисто условная запись и что в этом случае никакого числового значения такой предел не имеет и, следовательно, не существует, в смысле определения предела функции.

        Пример 2.24Примером бесконечно большой при может служить : в качестве окончания можно тогда взять . Очевидно, что тогда , если .

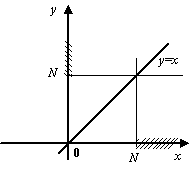
Рис.2.30.График

    

        Пример 2.25Примером положительной бесконечно большой при может служить .

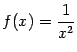Рис.2.31.График

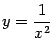
В качестве упражнения найдите зависимость числа , задающего окончание базы , от числа .

        Пример 2.26Примером отрицательной бесконечно большой при может служить функция .

Рис.2.32.График

В качестве упражнения найдите зависимость числа , задающего окончание базы , от числа .

Связь бесконечно больших и бесконечно малых величин устанавливает следующая теорема.

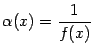        Теорема 2.16Пусть  -- функция, бесконечно большая при базе . Тогда величина  -- бесконечно малая при базе .

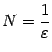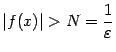        Доказательство.     Для начала заметим, что на всех достаточно далёких окончаниях базы будет , так что функция определена на этих окончаниях. Далее, пусть взято некоторое . Положим и выберем такое окончание , что при из этого окончания. Тогда 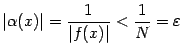при таких , что и означает, что .

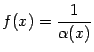        Замечание 2.9Утверждение, обратное к доказанной теореме, вообще говоря, неверно: если -- бесконечно малая при базе , то функция не всегда является бесконечно большой при базе , хотя бы потому, что может быть не определена ни на каком окончании базы . Простейший пример -- это постоянная величина , которая, очевидно, бесконечно мала при любой базе ( ), но не имеет смысла ни при каких . Однако если сделать дополнительное предположение, что при всех из некоторого окончания базы , то обратное утверждение становится верным.

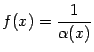        Теорема 2.17Пусть  -- такая бесконечно малая при базе , что при всех из некоторого окончания базы . Тогда функция  -- бесконечно большая при базе .    

Докажите эту теорему в качестве упражнения.

Утверждение, что некоторая функция является бесконечно большой положительной величиной при базе означает при вычислении пределов, что при замене база переходит в базу . Если же -- отрицательная бесконечно большая, то после замены получится база . Прослеживая за изменениями баз при последовательных заменах, можно вычислять многие пределы.

        Пример 2.27Найдём предел .

Рассмотрим замену . При будет 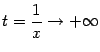. Пусть теперь . При будет . Наконец, пусть . При будет . (См. графики, расположенные ниже.) Последнее соотношение означает, что

(и что, вдобавок, величина остаётся положительной).

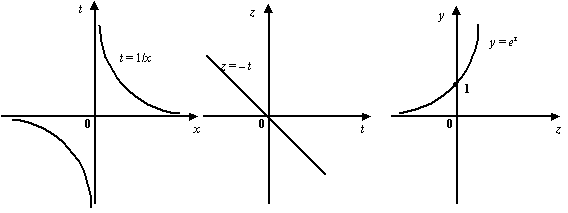
Рис.2.33.Графики зависимостей , ,

Заметим, что при решении было важно отследить изменение функций именно при , стремящемся к 0 справа. В качестве упражнения покажите, что если бы рассматривалась база , то получилась бы бесконечно большая положительная величина , а при базе величина не имеет никакого предела и не является бесконечно большой.

Использование непрерывности функций при вычислении пределов

Выше, в примерах 2.17 и 2.23, мы отмечали, что, фактически, при вычислении этих пределов использовали соображения, связанные с непрерывностью функций. Дадим теперь строгое определение непрерывности и обсудим способы вычисления пределов с помощью этого понятия.

        Определение 2.14Пусть -- внутренняя точка области определения функции , то есть функция определена при всех из некоторого интервала ( ), окружающего точку . Функция называетсянепрерывной в точке , если

(то есть предполагается, что этот предел существует и равен значению функции в указанной точке).    

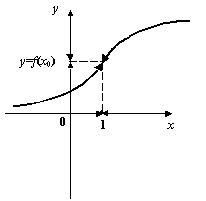
Рис.2.34.Функция непрерывна в точке CLX.ru - реклама в интернет

        Пример 2.28При доказательстве теоремы о первом замечательном пределе нами было получено, что (формула (2.3)). Так как , то с помощью замены легко показать, что а из теоремы о связи односторонних и двустороннего пределов отсюда следует, что

Эта формула означает, что функция непрерывна в точке .

Там же была получена формула (2.4): Пользуясь тем, что , и сделав замену , получим, что Поэтому и

Это означает, что функция также непрерывна при .

Покажем, что функция непрерывна при любом . По определению, для этого нужно доказать, что

Положим и заметим, что база при такой замене переходит в базу . Далее,

Поэтому

(здесь мы воспользовались линейностью предела; и были при этом постоянными коэффициентами), что и доказывает непрерывность синуса.

Совершенно аналогично, с использованием формулы

доказывается непрерывность при любом функции .

CLX.ru - реклама в интернет

        Определение 2.15Пусть функция определена на некотором полуинтервале ( ), примыкающем к точке справа. Функция называетсянепрерывной справа в точке , если существует предел , и

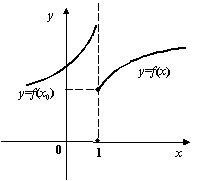
Рис.2.35.Функция непрерывна справа в точке

Пусть функция определена на некотором полуинтервале ( ), примыкающем к точке слева. Функция называетсянепрерывной слева в точке , если существует , и

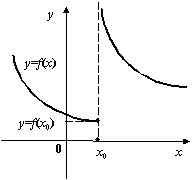
Рис.2.36.Функция непрерывна слева в точке

    

Из теоремы о связи односторонних пределов с двусторонним сразу следует такая

        Теорема 2.18Функция непрерывна в точке тогда и только тогда, когда она непрерывна справа в точке и непрерывна слева в точке .     

Поскольку , то непрерывность функции в точке означает, что обозначения функции и предела можно поменять местами:

(2.6)

То же касается и непрерывности слева и справа.

Назовём элементарнойлюбую функцию переменного из следующего списка:

(-- произвольные постоянные вещественные числа, ), а также любую функцию, полученную из этих элементарных функций при помощи композиций, арифметических операций, перехода к обратной функции.

При этом в число элементарных функций попадают, например, все многочлены

(где -- постоянные), все рациональные дроби

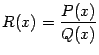
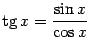(где и -- многочлены), а также , , (обратная к главной ветви ), (обратная к главной ветви ), (обратная к ) и другие функции, с которыми можно было встретиться ещё в школьном курсе анализа.

Однако не все функции, рассматривающиеся в курсе математического анализа, являются элементарными. Примером может служить довольно часто употребляющаяся функция

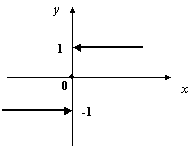
Рис.2.37.График функции

Если бы не значение , её можно было бы рассматривать как элементарную: при она совпадает с функцией

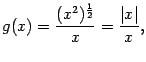
которая при не определена. Однако незначительное, на первый взгляд, отличие играет ключевую роль с точки зрения следующей теоремы.

        Теорема 2.19Любая элементарная функция непрерывна в любой точке своей области определения.

Частичное доказательство теоремы мы приведём ниже, в главе о свойствах непрерывных функций. Заметим, что выше мы уже доказали непрерывность функции . Полное доказательство теоремы можно найти в подробных учебниках по математическому анализу, например,Г. М. Фихтенгольц,Курс дифференциального и интегрального исчисления, т. 1илиС. М. Никольский,Курс математического анализа, т. 1.

В качестве примера рассмотрим только что введённую функцию 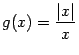. Её график таков:

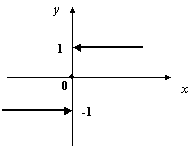
2.38.График функции

Для любой точки из области определения этой функции либо , и тогда при всех из некоторой окрестности точки , либо , и тогда при всех из некоторой окрестности точки . Очевидно, что тогда в первом случае

а во втором --

то есть функция непрерывна в любой точке своей области определения.

В случае функции всё дело "портит" точка : очевидно, что

то есть в точке 0 нет непрерывности справа. (Точно так же нет и непрерывности слева.)

Используя непрерывность элементарных функций, на основании общих теорем можно во многих (простых) случаях находить значение пределов прямой подстановкой предельного значения в выражение, стоящее под знаком предела. Именно так мы поступим при вычислении предела в следующем примере.

Пример 2.29Найдём предел .

Поскольку функция 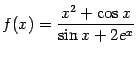-- элементарная, причём -- точка её области определения (так как ), то для нахождения предела достаточно воспользоваться равенством (2.6) и подставить вместо предельное значение 0:

    

Прямую подстановку использовать нельзя в тех случаях, когда мы не можем вычислить значение элементарной функции, стоящей под знаком предела, в данной предельной точке . В этом случае говорят, что задающее функцию выражение, а также и сам предел представляют собойнеопределённость. Выше мы уже встречались с неопределённостями вида . Бывают ещё неопределённости вида , , , и других видов, заданные выражениями, не имеющими формального смысла. С символами в этих выражениях нельзя обращаться, как с числами в обычных дробях, разностях, произведениях и т. д. В частности, "дроби" , вовсе не всегда означают пределы, значение которых равно единице. 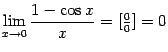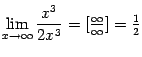Например, , а ; , а 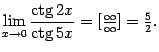(Вычислите все эти пределы в качестве упражнения.) "Разности" вида отнюдь не всегда обозначают неопределённости, которые после раскрытия предела дадут 0. Например, (здесь на самом деле получается 0), а .

Так что получается, что вся теория вычисления (нетривиальных) пределов -- это изучение способов раскрытия неопределённостей.

Во многих случаях, чтобы раскрыть неопределённость, достаточно каким-либо образом преобразовать стоящую под знаком предела функцию, после чего нахождение предела сводится к применению общих теорем (о пределе суммы, произведения, частного и т. п.), а также теорем о первом и втором замечательных пределах. Многие такие примеры мы разбирали выше. А вот ещё один типичный пример.

        Пример 2.30Найдём предел .

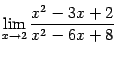Данный предел представляет собой неопределённость, так как при как числитель, так и знаменатель обращаются в 0 (это неопределённость вида ). Так что просто подставить 2 вместо в исходную дробь нельзя. Однако если разложить числитель и знаменатель на множители (для чего найдём корни числителя: и -- и знаменателя: и ), получим и , и видно, что дробь (при ) можно упростить, сократив на . Поскольку при мы считаем, что , то

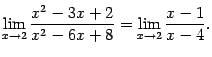
В последнем пределе дробь непрерывна при , так как точка 2 входит в область определения этой элементарной функции. Поэтому 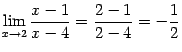и, следовательно,

    

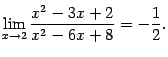
        Упражнение 2.7Найдите предел 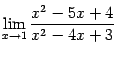. (При этом числитель и знаменатель можно сократить на . Ответ: .)

        Упражнение 2.8Найдите предел 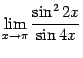. (При этом знаменатель можно представить в виде , а затем сократить дробь на . Ответ:0.)

Сравнение бесконечно малых

Определение 2.16Пусть фиксирована некоторая база и на некотором её окончании заданы две функции и , бесконечно малые при базе . Предположим также, что при всех . Пусть существует

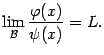
Если , то бесконечно малая имеет тот же порядок малости, что и . Этот факт обозначается так:

Если же , то имеет больший порядок малости, чем . Это обозначается так:

Заметим, что если , то для всех из некоторого окончания базы будет выполнено неравенство . Это сразу следует из того, что

Предложение 2.2Если при базе бесконечно малая имеет тот же порядок малости, что , то и имеет тот же порядок малости, что , то есть

(S)

CLX.ru - реклама в интернет

Если две бесконечно малых и одного порядка малости, и две бесконечно малых и тоже одного порядка малости при базе , то две величины и также имеют один и тот же порядок малости при базе , то есть

(T)

Кроме того, бесконечно малая величина имеет тот же порядок малости, что она же сама:

(R)

Доказательство. Поскольку 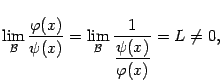то 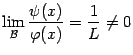, откуда следует первое из доказываемых утверждений.

Второе утверждение следует из первого и цепочки равенств

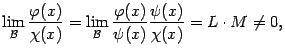
где

по условию предложения.

Наконец, третье утверждение сразу следует из очевидного соотношения

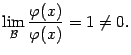
Итак, свойство двух или нескольких бесконечно малых величин иметь один и тот же порядок малости, то есть отношение , заданное в множестве бесконечно малых при данной базе величин , являетсярефлексивным,транзитивнымисимметричным.

Рефлексивностькакого-либо отношения , заданного в некотором множестве объектов , означает, что выполнено свойство (R): ,транзитивность-- что выполнено свойство (T): , асимметричность-- что выполнено свойство (S): .

Любое рефлексивное, транзитивное и симметричное отношение разбивает множество объектов, для которых оно определено, наклассы объектов, эквивалентных по данному отношению: в один класс с объектом попадают все объекты , для которых .

CLX.ru - реклама в интернет

Поэтому все бесконечно малые при данной базе величины разбиваются на классы по отношению , в каждый из которых входят все величины, имеющие один и тот же порядок малости.

Пример 2.31При базе величины и , где и , , имеют один и тот же порядок малости (так как, очевидно, их отношение постоянно и его предел 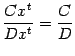постоянно и его предел равен . Например, при величины и имеют один и тот же порядок малости.

При базе величина имеет больший порядок малости, чем , при :

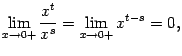
так как . Если степени и определены и при , то аналогичное утверждение верно и для двусторонней базы . Например, при величина -- большего порядка малости, чем . При величина -- большего порядка малости, чем , а -- величина большего порядка малости, чем .

Пример 2.32Три величины , , являются бесконечно малыми при базе . Так как нетрудно проверить, что

то и имеют один и тот же порядок малости при .

Поскольку

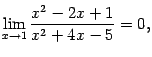
то величина имеет больший порядок малости, нежели , и не относится к тому классу, к которому принадлежат и .

Пример 2.33Используя первый замечательный предел, легко видеть, что при и

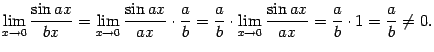
Это означает, что величины и имеют один и тот же порядок малости при .

Предложение 2.3Если имеет при базе больший порядок малости, чем , а -- такой же порядок малости, что и , то имеет больший порядок малости, чем .

Доказательство. Для доказательства напишем такую цепочку равенств:

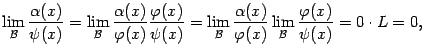
что и доказывает предложение.

Пример 2.34Поскольку, как мы видели в примерах выше, и , то -- величина большего порядка малости, чем .

Определение 2.17Пусть и -- бесконечно малые при базе и

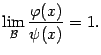
Тогда бесконечно малая называетсяэквивалентнойбесконечно малой при базе . Это обозначается следующим образом:

Очевидно, что если величина эквивалентна величине , то они имеют один и тот же порядок малости (так как при этом ). Кроме того, свойство двух бесконечно малых величин быть эквивалентными, то есть отношение , (так же, как и отношение ) рефлексивно, транзитивно и симметрично. А именно, имеет место

Предложение 2.4Если при базе бесконечно малая эквивалентна бесконечно малой , то и эквивалентна :

(S)

Если две бесконечно малых и эквивалентны, и две бесконечно малых и тоже эквивалентны при базе , то две величины и также эквивалентны при базе :

(T)

Кроме того, величина эквивалентна себе самой:

(R)

Доказательствоповторяет доказательство предложения 2.2.Нужно только учесть, что .

Итак, отношение эквивалентности обладает свойствами симметричности (S), транзитивности (T) и рефлексивности (R) и, следовательно, разбивает множество всех бесконечно малых при данной базе величин на классы эквивалентных между собой бесконечно малых. Эти классы более мелкие, чем классы бесконечно малых величин одного порядка малости, на которые то же самое множество бесконечно малых разбивается отношением .

Пример 2.35Согласно первому замечательному пределу, 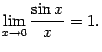Это означает, что

Кроме того, в примере 2.20 мы показали, что 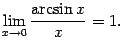Это означает, что

Польза для вычисления пределов от использования эквивалентности бесконечно малых, а также от бесконечно малых большего порядка выражается следующими утверждениями.

Предложение 2.5Пусть существует предел где и -- бесконечно малые при базе . Пусть также и . Тогда существует предел

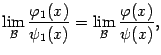
то есть бесконечно малые как в числителе, так и в знаменателе неопределённости вида можно заменять на эквивалентные им бесконечно малые: величина предела от этого не изменится.

Доказательство. Для доказательства напишем такое равенство:

и заметим, что эквивалентность величин и , и означает, что первый и последний пределы в правой части этой формулы равны1.

Совершенно так же доказывается уточнение доказанного только что предложения. Это уточнение означает, что заменять эквивалентными можно не только числитель или знаменатель целиком, но и любой бесконечно малый множитель в числителе или знаменателе:

Предложение 2.6Пусть , и существует предел

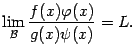
Тогда и можно заменить на эквивалентные, и значение предела не изменится, то есть

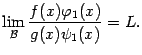
Предложение 2.7Пусть , и существует предел . Тогда существует предел

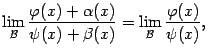
то есть бесконечно малые большего порядка можно отбрасывать как в числителе, так и в знаменателе неопределённости вида величина предела от этого не изменится.

Доказательство. Согласно предложению 2.5, достаточно доказать, что если , то . Но это следует из такой цепочки равенств:

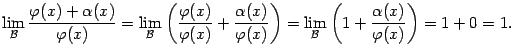
Пример 2.36Вычислим предел

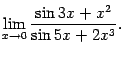
Для этого заметим, что, как мы проверяли выше, -- величина большего порядка малости, чем . Аналогично проверяется, что -- величина большего порядка малости, чем . Поскольку слагаемые большего порядка малости можно отбросить, то

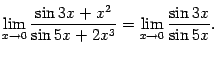
Далее, поскольку , очевидно, эквивалентен (согласно первому замечательному пределу), а эквивалентен , то последний предел можно упростить, заменив бесконечно малые в числителе и знаменателе на эквивалентные им, а затем сократить на:

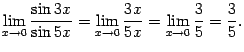
При вычислении пределов часто бывают полезны также следующие два утверждения.

Предложение 2.8Пусть и . Тогда: 1) и 2) при любом (в случае, если степень определена только при , нужно потребовать, чтобы выполнялось неравенство .

(Заметим, что второе утверждение не следует из первого, поскольку -- не обязательно целое число.)

Доказательство. Первое утверждение означает, согласно определению эквивалентности, что

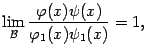
если известно, что

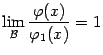
и

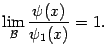
Но это сразу следует из теоремы о пределе произведения ( теорема 2.9).

Второе утверждение означает, что

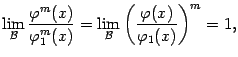
если известно, что

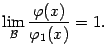
Это следует из того, что степенная функция непрерывна при любом , если . Как отмечалось выше, для непрерывной функции можно переставлять местами знак функции и знак предела:

В случае степенной функции , сделав замену переменного и связанную с ней замену базы, мы получим, что

Беря 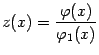, получаем, что

что и требовалось доказать.

Таблица эквивалентных бесконечно малых при

Как показывает приведённый выше пример 2.36, пределы отношения бесконечно малых можно упрощать, откидывая бесконечно малые слагаемые большего порядка и заменяя множители в числителе и знаменателе на эквивалентные бесконечно малые. Для того, чтобы этот способ вычисления пределов (точнее, раскрытия неопределённостей вида ) можно было применять к возможно большему числу примеров, мы должны иметь достаточно большой запас известных пар эквивалентных бесконечно малых величин. Для наиболее употребительной базы создадим такой запас в виде таблицы "стандартных" эквивалентных бесконечно малых.

Поскольку в этой таблице мы всегда будем рассматривать базу , для простоты записи обозначение этой базы будем пропускать и писать знак вместо .

1) . Эту формулу мы уже доказали и использовали в примерах. Эквивалентность и при означает в точности, что первый замечательный предел равен 1.

2) . Эта эквивалентность тоже была доказана выше в одном из примеров.

3) . Докажем эту эквивалентность: