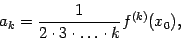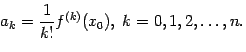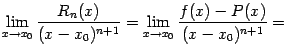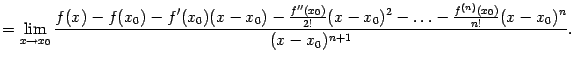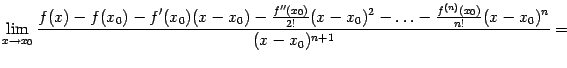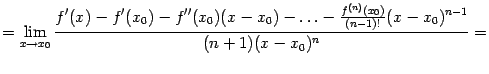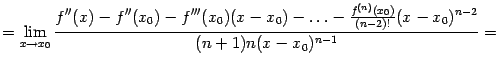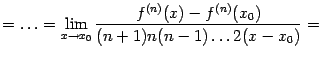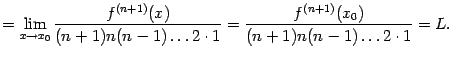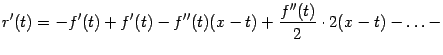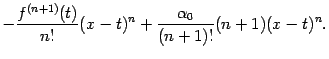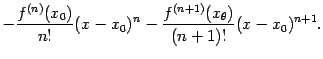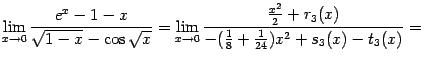- •Функции и их графики Конспекты, лекции, задачи
- •Первый способ задания функции: табличный
- •Clx.Ru - реклама в интернет
- •Упражнения
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
- •Сводка основных результатов о производных
- •Формула Тейлора теория и практика в примерах Многочлен Тейлора
- •Исследование функций и построение графиков Асимптоты графика функции
- •Достаточные условия локального экстремума
- •Примеры исследования функций и построения графиков
Формула Тейлора теория и практика в примерах Многочлен Тейлора
Многочлен
![]() ,
наиболее подходящий (с некоторой точки
зрения) для этой цели, называетсямногочленом Тейлорадля данной
функции; найдя его по заданной функции
,
наиболее подходящий (с некоторой точки
зрения) для этой цели, называетсямногочленом Тейлорадля данной
функции; найдя его по заданной функции
![]() ,
мы сможем вместо сложного вычисления
значений функции
,
мы сможем вместо сложного вычисления
значений функции
![]() приближённо
заменять это вычисление на вычисление
значений многочлена
приближённо
заменять это вычисление на вычисление
значений многочлена
![]() .
.
Уточним теперь постановку задачи. Пусть
функция
![]() определена
в некоторой окрестности
определена
в некоторой окрестности
![]() некоторой
точки
некоторой
точки
![]() и
имеет всюду в окрестности
и
имеет всюду в окрестности
![]() производные
производные
![]() при
при
![]() .Многочленом Тейлорастепени
.Многочленом Тейлорастепени
![]() в
точке
в
точке
![]() называется
такой многочлен
называется
такой многочлен
![]() степени
степени
![]() ,
такой, что его значение и значение всех
его производных, вычисленные в точке
,
такой, что его значение и значение всех
его производных, вычисленные в точке
![]() ,
равны соответствующим значениям функции
,
равны соответствующим значениям функции
![]() и
её производных
и
её производных
![]() до
порядка
до
порядка
![]() в
этой же точке:
в
этой же точке:
![]()
Если это условие совпадения выполнено,
то графики функций
![]() и
и
![]() ,
по крайней мере при
,
по крайней мере при
![]() ,
близких к
,
близких к
![]() ,
будут идти весьма тесно друг к другу.
Равенство
,
будут идти весьма тесно друг к другу.
Равенство
![]()
означает, что графики проходят через
одну и ту же точку
![]() ;
равенство
;
равенство
![]()
означает, что эти графики имеют в этой общей точке совпадающие касательные (так как общее значение производной -- это общий угловой коэффициент касательной); равенство
![]()
означает, как мы убедимся ниже, что эти графики имеют в общей точке одинаковую кривизну, и т. д.
Для нахождения вида многочлена Тейлора
для заданной функции сделаем сначала
следующее замечание. Любой многочлен
![]() степени
степени
![]() вида
вида
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
можно представить в виде, расположенном
по степеням бинома
![]() :
:
![]()
и наоборот, раскрыв скобки в последней
формуле, мы можем получить многочлен
по степеням
![]() .
.
Действительно, положив
![]() ,
мы можем подставить
,
мы можем подставить
![]() в
правую часть формулы
в
правую часть формулы
![]() ,
раскрыть степени
,
раскрыть степени
![]() при
при
![]() по
формуле бинома Ньютона, а потом привести
подобные члены. Все коэффициенты
по
формуле бинома Ньютона, а потом привести
подобные члены. Все коэффициенты
![]() (кроме
(кроме
![]() )
и свободный член при этом изменятся на
некоторые другие (
)
и свободный член при этом изменятся на
некоторые другие (![]() в нашей формуле), но получится многочлен
по степеням бинома
в нашей формуле), но получится многочлен
по степеням бинома
![]() ,
имеющий ту же степень
,
имеющий ту же степень
![]() .
.
Итак, будем предполагать, что многочлен Тейлора мы ищем в виде
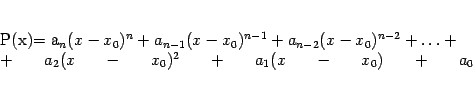
при некоторых коэффициентах
![]() ,
пока не известных. Отыщем значения этихкоэффициентов Тейлора
,
пока не известных. Отыщем значения этихкоэффициентов Тейлора
![]() по
значениям производных данной функции
в точке
по
значениям производных данной функции
в точке
![]() .
.
Учтём требование к значению многочлена:
![]() .
Подставив в равенство (Тейлор
1)
.
Подставив в равенство (Тейлор
1)
![]() ,
получим, что
,
получим, что
![]() ,
так как все остальные слагаемые обратятся
в 0. Тем самым
,
так как все остальные слагаемые обратятся
в 0. Тем самым
![]()
Учтём затем требование к значению первой
производной многочлена: . Производная
от
![]() равна
равна

Подставив в равенство (Тейлор
2) значение
![]() ,
получим, что
,
получим, что
![]() ,
так как снова все остальные слагаемые
обратятся в 0. Отсюда
,
так как снова все остальные слагаемые
обратятся в 0. Отсюда
![]()
Следующее требование -- к значению
второй производной многочлена:
![]() .
Вторая производная от
.
Вторая производная от
![]() равна
равна
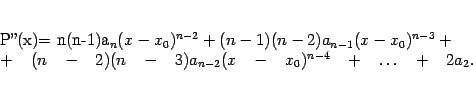
Снова подставив в равенство (Тейлор
3) значение
![]() ,
получим, что
,
получим, что
![]() ,
откуда
,
откуда
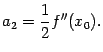
Далее нетрудно сообразить, что получится
![]() ,
откуда
,
откуда
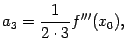
и вообще,
|
|
|
при
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
..., последнюю формулу можно записать в
виде
,
..., последнюю формулу можно записать в
виде
|
|
|
Итак, мы получили, что многочлен Тейлора
для функции
![]() в
точке
в
точке
![]() имеет
вид
имеет
вид
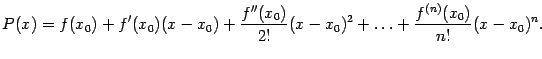
Остаток в формуле Тейлора и его оценка
Разность между функцией
![]() и
её многочленом Тейлора называется
и
её многочленом Тейлора называется
![]() -м
остатком, или
-м
остатком, или
![]() -м
остаточным членом; обозначим этот
остаток через
-м
остаточным членом; обозначим этот
остаток через
![]() :
:
![]()
Формула
![]() ,
в более развёрнутой форме имеющая вид
,
в более развёрнутой форме имеющая вид
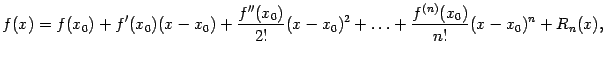
называется формулой Тейлорадля
функции
![]() в
точке
в
точке
![]() ,
а представление функции
,
а представление функции
![]() в
таком виде -- её разложением по формуле
Тейлора.
в
таком виде -- её разложением по формуле
Тейлора.
Если считать, что остаток
![]() мал,
то его можно отбросить без большой
погрешности; при этом получается
приближённая формула
мал,
то его можно отбросить без большой
погрешности; при этом получается
приближённая формула
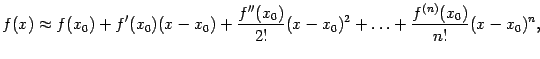
дающая возможность для приближённого
нахождения значений функции
![]() .
.
Выясним, в каком смысле можно понимать
"малость" остатка
![]() в
формуле Тейлора, чтобы этой приближённой
формулой мы могли пользоваться осмысленно.
в
формуле Тейлора, чтобы этой приближённой
формулой мы могли пользоваться осмысленно.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Теорема 6.1(формула Тейлора с остаточным членом в
форме Пеано)Пусть
![]() --
остаток в формуле Тейлора для функции
--
остаток в формуле Тейлора для функции
![]() в
точке
в
точке
![]() ,
и функция
,
и функция
![]() имеет
непрерывную
имеет
непрерывную
![]() -ю
производную. Тогда
-ю
производную. Тогда
![]() --
бесконечно малая величина того же или
большего порядка малости, как
--
бесконечно малая величина того же или
большего порядка малости, как
![]() ,
при
,
при
![]() .
(Остаточный член
.
(Остаточный член
![]() ,
о котором известны эти сведения о порядке
малости, называется остаточным
членом в форме Пеано.)
,
о котором известны эти сведения о порядке
малости, называется остаточным
членом в форме Пеано.)
Доказательство. Утверждение теоремы означает, что существует
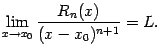
При
![]() остаток
остаток
![]() будет
иметь тот же порядок малости, что
будет
иметь тот же порядок малости, что
![]() ,
а при
,
а при
![]() --
больший порядок малости. Итак, вычислим
предел:
--
больший порядок малости. Итак, вычислим
предел:
|
|
|
|
|
|
Применим к этому пределу правило
Лопиталя, повторив этот приём
![]() раз:
раз:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последний предел мы вычислили прямой
подстановкой, поскольку по предположению
![]() --
непрерывная функция. Существование
предела доказывает утверждение теоремы.
--
непрерывная функция. Существование
предела доказывает утверждение теоремы.
Доказанная теорема утверждает, что при
малых отклонениях от
![]() значения
значения
![]() будут
отклоняться от
будут
отклоняться от
![]() не
более чем на величину
не
более чем на величину
![]() -го
порядка малости относительно разности
-го
порядка малости относительно разности
![]() ,
что даёт нам уверенность в том, что
замена
,
что даёт нам уверенность в том, что
замена
![]() на
многочлен Тейлора
на
многочлен Тейлора
![]() будет
давать очень хорошее приближение, и это
приближение будет улучшаться, если мы
будем увеличивать значения
будет
давать очень хорошее приближение, и это
приближение будет улучшаться, если мы
будем увеличивать значения
![]() .
Однако доказанная теорема не даёт нам
оценки остатка
.
Однако доказанная теорема не даёт нам
оценки остатка
![]() .
Этот пробел устраняет следующая теорема.
.
Этот пробел устраняет следующая теорема.
Теорема 6.2(остаток в формуле Тейлора в форме
Лагранжа)Пусть при всех
![]() существует
существует
![]() -я
производная
-я
производная
![]() .
Тогда для любого
.
Тогда для любого
![]() существует
точка
существует
точка
![]() ,
лежащая между
,
лежащая между
![]() и
и
![]() (то
есть
(то
есть
![]() при
при
![]() ),
такая что
),
такая что
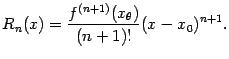
(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)
Доказательство.
Это доказательство не столь прямолинейное,
как в предыдущей теореме. Рассмотрим
вспомогательную функцию
![]() переменного
переменного
![]() ,
изменяющегося в рассматриваемой
окрестности
,
изменяющегося в рассматриваемой
окрестности
![]() точки
точки
![]() .
Эта функция будет зависеть также от
параметра
.
Эта функция будет зависеть также от
параметра
![]() :
:
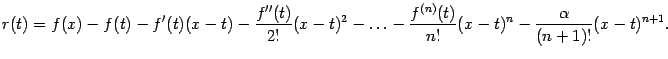
Подберём такое значение параметра
![]() ,
равное
,
равное
![]() ,
чтобы при
,
чтобы при
![]() функция
обращалась в 0:
функция
обращалась в 0:
![]() .
Фиксируем такое значение
.
Фиксируем такое значение
![]() .
.
Тогда функция
![]() удовлетворяет
условиям теоремы Ролля на отрезке
удовлетворяет
условиям теоремы Ролля на отрезке
![]() (или
(или
![]() ,
если
,
если
![]() ):
):
![]() ,
что очевидно по определению функции
,
что очевидно по определению функции
![]() ;
;
![]() согласно
выбору параметра; дифференцируемость
на
согласно
выбору параметра; дифференцируемость
на
![]() и
непрерывность в точках
и
непрерывность в точках
![]() и
и
![]() следуют
из предположенных свойств функции
следуют
из предположенных свойств функции
![]() .
По теореме Ролля существует такая точка
.
По теореме Ролля существует такая точка
![]() ,
что
,
что
![]()
Однако нетрудно подсчитать, находя
производные произведений в определении
функции
![]() ,
что
,
что
|
|
|
|
|
|
Все слагаемые в начале правой части, включая обозначенные многоточием, взаимно уничтожаются, так что получаем
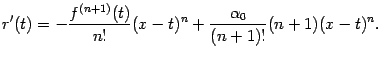
Подстановка
![]() даёт
даёт
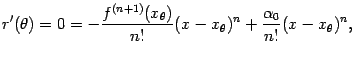
откуда следует, что
![]()
Теперь вспомним, что значение параметра
мы выбрали так, что
![]() .
Подставив найденное значение
.
Подставив найденное значение
![]() в
выражение для
в
выражение для
![]() ,
получим:
,
получим:
|
|
|
|
|
|
Отсюда получаем, наконец,
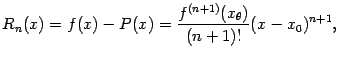
что и требовалось доказать.
Замечание
6.1Полученную в предыдущей теореме
оценку остатка удобно применять для
оценки погрешности при замене функции
её многочленом Тейлора, если известно,
что
![]() -я
производная при всех
-я
производная при всех
![]() из
рассматриваемого интервала ограничена
по абсолютной величине некоторым числом:
из
рассматриваемого интервала ограничена
по абсолютной величине некоторым числом:
![]()
Тогда
![]()
и при каждом фиксированном
![]() мы
можем узнать оценку погрешности
приближённой формулы
мы
можем узнать оценку погрешности
приближённой формулы
![]() .
.
Замечание
6.2Мы всюду подчёркивали, что
приближённая формула
![]() имеет
место только при малых значениях
отклонения
имеет
место только при малых значениях
отклонения
![]() .
Надежды на то, что при увеличении
.
Надежды на то, что при увеличении
![]() интервал,
на котором можно будет применять с
заданной точностью эту приближённую
формулу, будет расширяться, вообще
говоря, не оправдываются. Для пояснения
сказанного приведём пример.
интервал,
на котором можно будет применять с
заданной точностью эту приближённую
формулу, будет расширяться, вообще
говоря, не оправдываются. Для пояснения
сказанного приведём пример.
Пусть рассматривается функция
![]() ,
доопределённая при
,
доопределённая при
![]() по
непрерывности:
по
непрерывности:
![]() .
Ранее мы уже рассматривали эту функцию
и выяснили, что все её производные
существуют на всей оси
.
Ранее мы уже рассматривали эту функцию
и выяснили, что все её производные
существуют на всей оси
![]() и
при
и
при
![]() равны
0:
равны
0:
![]() при
всех
при
всех
![]() .
Это означает, что при любом порядке
.
Это означает, что при любом порядке
![]() многочлена
Тейлора все его коэффициенты
многочлена
Тейлора все его коэффициенты
 равны
0, и формула Тейлора сводится к равенству
равны
0, и формула Тейлора сводится к равенству
![]() .
Таким образом, любой остаток в формуле
Тейлора для этой функции в точке 0 равен
одному и тому же, а именно, самой функции
.
Таким образом, любой остаток в формуле
Тейлора для этой функции в точке 0 равен
одному и тому же, а именно, самой функции
![]() !
Поэтому уменьшить остаток за счёт
увеличения
!
Поэтому уменьшить остаток за счёт
увеличения
![]() здесь
никак не возможно: единственным
приближением, которое формула Тейлора
даёт для функции
здесь
никак не возможно: единственным
приближением, которое формула Тейлора
даёт для функции
![]() ,
здесь служит тождественный 0.
,
здесь служит тождественный 0.
Формула Тейлора для некоторых элементарных функций
Рассмотрим несколько важнейших
элементарных функций и найдём для них
многочлены Тейлора при
![]() .
.
1. Рассмотрим функцию
![]() .
Все её производные совпадают с ней:
.
Все её производные совпадают с ней:
![]() ,
так что коэффициенты Тейлора в точке
,
так что коэффициенты Тейлора в точке
![]() равны
равны
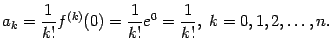
Поэтому формула Тейлора для экспоненты такова:
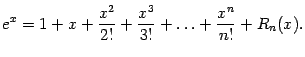
2. Рассмотрим функцию
![]() .
Её производные чередуются в таком
порядке:
.
Её производные чередуются в таком
порядке:
![]()
а затем цикл повторяется. Поэтому при
подстановке
![]() также
возникает повторение:
также
возникает повторение:
![]()
и т. д. Все производные с чётными
номерами оказываются равными 0; производные
с нечётными номерами
![]() равны
1 при
равны
1 при
![]() ,
то есть при
,
то есть при
![]() ,
и
,
и
![]() при
при
![]() ,
то есть при
,
то есть при
![]() .
Таким образом,
.
Таким образом,
![]() при
всех
при
всех
![]() и
коэффициенты Тейлора равны
и
коэффициенты Тейлора равны

Получаем формулу Тейлора для синуса:
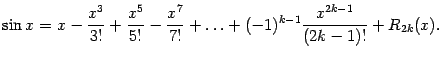
Заметим, что мы можем записать остаточный
член
![]() вместо
вместо
![]() (как
можно было бы подумать), поскольку можно
считать, что слагаемое порядка
(как
можно было бы подумать), поскольку можно
считать, что слагаемое порядка
![]() ,
с коэффициентом, равным 0, тоже включено
в многочлен Тейлора.
,
с коэффициентом, равным 0, тоже включено
в многочлен Тейлора.
3. Для функции
![]() производные
также чередуются с циклом длины 4, как
и для синуса. Значения в точке
производные
также чередуются с циклом длины 4, как
и для синуса. Значения в точке
![]() имеют
то же чередование:
имеют
то же чередование:
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
|
|
|
|
|
|
Нетрудно видеть, что
![]() при
при
![]() ,
,
![]() и
и
![]() при
при
![]() ,
,
![]() .
Поэтому разложение косинуса по формуле
Тейлора имеет вид
.
Поэтому разложение косинуса по формуле
Тейлора имеет вид
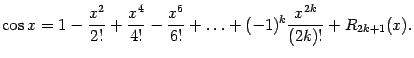
Здесь мы также считаем, что последним
в многочлене Тейлора выписано слагаемое,
содержащее
![]() с
нулевым коэффициентом.
с
нулевым коэффициентом.
Упражнение
6.1Найдите формулу для производной
произвольного порядка от функции
![]() .
Вычислите значения этих производных
при
.
Вычислите значения этих производных
при
![]() и
коэффициенты Тейлора. Покажите, что
имеет место разложение
и
коэффициенты Тейлора. Покажите, что
имеет место разложение
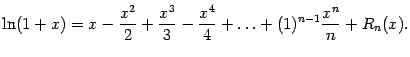
Упражнение
6.2Найдите формулу для производной
произвольного порядка от функции
![]() при
фиксированном
при
фиксированном
![]() .
Вычислите значения этих производных
при
.
Вычислите значения этих производных
при
![]() и
коэффициенты Тейлора. Покажите, что
имеет место разложение
и
коэффициенты Тейлора. Покажите, что
имеет место разложение
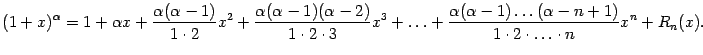
Упражнение
6.3Покажите, что разложения по
формуле Тейлора для функций
![]() и
и
![]() выглядят
так:
выглядят
так:
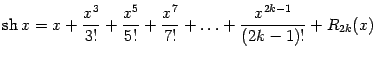
и
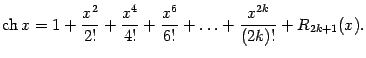
Сравните найденные разложения с
разложениями для
![]() ,
,
![]() и
и
![]() .
.
На основе полученных разложений можно получать и разложения многих других функций.
Пример 6.1Рассмотрим функцию
![]() .
Найдём её разложение по формуле Тейлора
в точке
.
Найдём её разложение по формуле Тейлора
в точке
![]() .
Начнём с того, что напишем ранее найденное
разложение для экспоненты,
.
Начнём с того, что напишем ранее найденное
разложение для экспоненты,
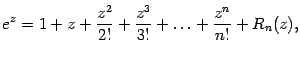
и положим в нём
![]() :
:
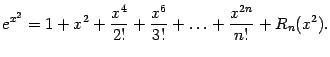
Теперь умножим левую и правую части
этой формулы на
![]() :
:
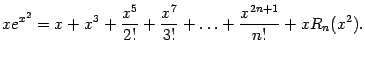
Заметим, что бесконечно малое при
![]() выражение
выражение
![]() имеет
тот же или больший порядок малости, как
имеет
тот же или больший порядок малости, как
![]() ,
и поэтому может рассматриваться как
остаточный член
,
и поэтому может рассматриваться как
остаточный член
![]() в
формуле Тейлора для
в
формуле Тейлора для
![]() ,
а предыдущие слагаемые в правой части
формулы -- как многочлен Тейлора
данной функции. Так что её искомое
разложение найдено.
,
а предыдущие слагаемые в правой части
формулы -- как многочлен Тейлора
данной функции. Так что её искомое
разложение найдено.
Разберём теперь пример того, как полученные разложения элементарных функций можно использовать для раскрытия некоторых неопределённостей.
Пример 6.2Найдём предел
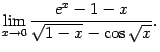
Для начала найдём разложение по формуле Тейлора в точке 0 для числителя:
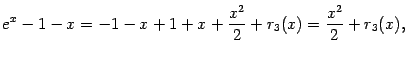
где через
![]() обозначен
остаточный член, имеющий тот же порядок
малости, что и
обозначен
остаточный член, имеющий тот же порядок
малости, что и
![]() .
Разложение для знаменателя имеет вид:
.
Разложение для знаменателя имеет вид:

где остаточные члены
![]() и
и
![]() тоже
имеют тот же порядок малости, что и
тоже
имеют тот же порядок малости, что и
![]() ,
при
,
при
![]() .
Выполняя приведение подобных членов,
получаем, что знаменатель равен
.
Выполняя приведение подобных членов,
получаем, что знаменатель равен
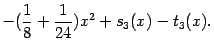
Итак,
|
|
|
|
|
|
Заметим, что этот способ раскрытия
неопределённостей типа
![]() в
некоторых случаях, подобных разобранному
в примере, менее трудоёмок, чем применение
правила Лопиталя.
в
некоторых случаях, подобных разобранному
в примере, менее трудоёмок, чем применение
правила Лопиталя.
Оценки ошибок в формулах приближённого дифференцирования
Используя оценку остаточного члена в
форме Лагранжа, можно провести анализ
погрешности в формулах приближённого
дифференцирования, предполагая шаг
![]() малым.
малым.
Пусть функция
![]() разложена
по формуле Тейлора, с остаточным членом
в форме Лагранжа, в точке
разложена
по формуле Тейлора, с остаточным членом
в форме Лагранжа, в точке
![]() .
Положим
.
Положим
![]() ,
тогда
,
тогда
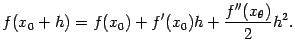
Отсюда
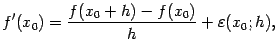
где
 --
--
погрешность формулы приближённого
дифференцирования, получающаяся при
замене
![]() на
разностную производную
на
разностную производную
 .
.
Следовательно,
![]()
где
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Как правило, заранее известна более
грубая оценка для
![]() на
некотором отрезке
на
некотором отрезке
![]() ,
включающем в себя
,
включающем в себя
![]() :
:
![]()
и
![]() не
зависит от
не
зависит от
![]() и
и
![]() .
Тогда
.
Тогда
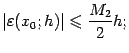
из этой оценки и определяют погрешность
вычислений при данном шаге
![]() .
.
Аналогично, можно получить оценку погрешности для разностной производной вида
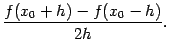
Ошибку
![]() при
замене
при
замене
![]() на
это отношение можно оценить исходя из
разложения
на
это отношение можно оценить исходя из
разложения
![]() в
точке
в
точке
![]() по
формуле Тейлора с остаточным членом в
форме Лагранжа порядка 3:
по
формуле Тейлора с остаточным членом в
форме Лагранжа порядка 3:
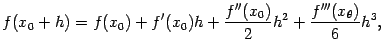
где
![]() .
Подставляя сюда
.
Подставляя сюда
![]() вместо
вместо
![]() ,
получаем:
,
получаем:
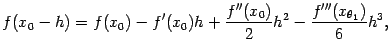
где
![]() .
Вычтем из первой формулы вторую:
.
Вычтем из первой формулы вторую:
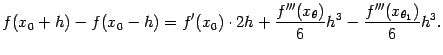
Отсюда
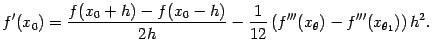
Если теперь предположить, что
![]()
то оценка погрешности получится такая:
Упражнение
6.4Исследуйте приближённую формулу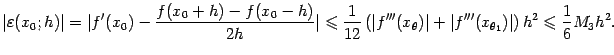
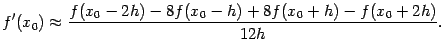
Какая степень приращения
![]() будет
множителем в оценке ошибки
будет
множителем в оценке ошибки
![]() ?
Оценки каких производных войдут в
формулу для оценки ошибки?
?
Оценки каких производных войдут в
формулу для оценки ошибки?
Упражнения
Упражнение
6.5Найдите разложение по формуле
Тейлора в точке
![]() функций
а)
функций
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
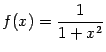 ;
з)
;
з)
![]() .
.
Ответы:
а)
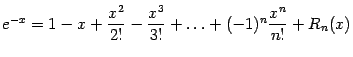 ;
;
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
б)
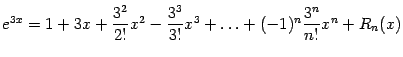 ;
;
в)
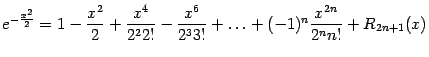 ;
;
г)
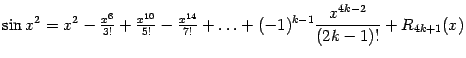 ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
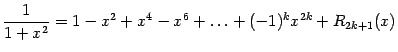 ;
;
з)
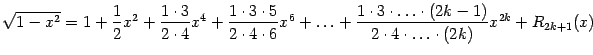 .
.
Упражнение
6.6Найдите следующие пределы,
применив разложение числителя и
знаменателя по формуле Тейлора:
а)
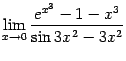 ;
б)
;
б)
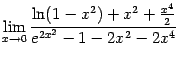 .
.
Ответы:а)
![]() ;
б)
;
б)
![]() .
.