Clx.Ru - реклама в интернет

Теорема 2.2Пусть -- некоторая база и -- некоторая функция, определённая на каком-нибудь окончании базы . Тогда множество -- это тоже база.

Доказательство. Во-первых, все множества не пусты, так как не пусты множества : если , то содержит, по крайней мере, точку . Осталось показать, во-вторых, что если и (где )-- два множества из , то найдётся такое множество ( ), что . Множество , по определению, состоит из всех точек , где и одновременно, то есть . Рассмотрим теперь некоторое окончание (такое окончание найдётся, по определению базы ) и соответствующее множество . Тогда все значения при будут среди значений при , то есть , что и требовалось показать.

Иногда получается, что если -- одна из знакомых нам рассмотренных выше баз, то и -- это тоже база известного типа.

Пример 2.5Пусть производится замена , где . Здравый смысл подсказывает нам, что если приближается к 2 и , то значения будут приближаться к , то есть база при такой замене переходит в базу . Это, конечно, верный результат но не всё так просто, как покажут нам следующие два примера.

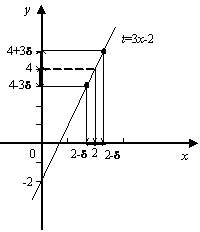
Рис.2.13.Преобразование базы при замене

CLX.ru - реклама в интернет

Пока что проверим формально результат, полученный нами с помощью интуитивных представлений о "стремлении". Пусть -- это произвольное окончание базы . Посмотрим, во что это множество перейдёт при действии функции . Поскольку эта линейная функция возрастает (её угловой коэффициент 3 положителен), то точки будут лежать между теми, в которые переходят концы интервала, то есть между и , и не будут совпадать с . Тем самым получили, что . При произвольном получаем произвольную проколотую окрестность точки 4 с полушириной : . Очевидно, что набор множеств -- это база , как мы и предполагали, исходя из интуитивных соображений.

Пример 2.6Пусть производится замена и . Рассуждая, как в предыдущем примере, получаем, что, наверное, тоже стремится к 0, то есть нужно рассматривать базу . Это, однако, не вполне верно. Следующий чертёж показывает, что образами окончаний базы служат не проколотые окрестности точки (являющиеся окончаниями базы ), а интервалы , где , примыкающие на оси (если её расположить горизонтально) справа к точке .

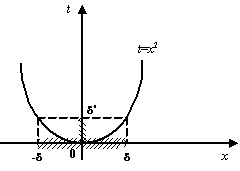
Рис.2.14.График и преобразование базы в базу

Набор таких интервалов образует правостороннюю базу , а не двустороннюю базу , как мы поторопились предположить. В некоторых примерах разница между этими базами может быть существенной при вычислении предела.

(Ниже мы рассмотрим предел , в котором эта разница существенна.)

Пример 2.7Пусть производится замена при базе . Интуитивно ясно, что когда приближается к1, то и тоже будет приближаться к1, причём "ловушки" предыдущего примера здесь нет: так как при функция возрастает, то при и близких к1 будет получаться , близкое к1, а при и близких к1 будет получаться , близкое к1. Поэтому должна бы, вроде, при такой замене получиться база . Однако и это не вполне так. Глядя на следующий чертёж, можно заметить, что образ окончания -- это множество

Эти два интервала, примыкающие к точке 1 слева и справа, имеют разную длину: левый имеет длину , а правый-- длину , то есть левый короче правого на .

Рис.2.15.График и преобразование базы

Однако по определению базы окончания этой базы состоят из пары примыкающих к точке 1симметричныхинтервалов! Так что формально получилась не база , а нечто на неё похожее, но не совсем то же самое.

На самом деле получившаяся в этом примере после замены база эквивалентнабазе в смысле следующего определения.

Определение 2.8Две базы и назовёмэквивалентными, если в любом окончании содержится некоторое окончание , и наоборот, в любом окончании содержится некоторое окончание .

Базы и , рассмотренные в предыдущем примере, эквивалентны, так как любое несимметричное окончание базы , имеющее, как мы выяснили, вид , содержится в симметричном окончании и содержит симметричное окончание базы .

Пределы, вычисленные по эквивалентным базам, совпадают, так что эквивалентные базы нет смысла отличать друг от друга. В этом мы убедимся, доказав следующую теорему.

Теорема 2.3Пусть и -- две эквивалентные базы, и существует . Тогда предел тоже существует, и .

Доказательство. Пусть фиксировано число . Так как по предположению теоремы , то для этого можно указать такое окончание базы , при любом из которого будет . Поскольку база эквивалентна базе , найдётся окончание , такое что следовательно, при любом . Значит, , что и требовалось доказать.

Итак, вычисление пределов по эквивалентным базам даёт один и тот же результат, и в дальнейшем мы не будем различать эквивалентные базы, в том числе и при их обозначении. В частности, все базы, эквивалентные введённой выше базе , мы будем тоже обозначать , все базы, эквивалентные введённой выше базе ,-- обозначать , ит.п.

Бесконечно малые и локально ограниченные величины и их свойства

В этом разделе мы изучим свойства бесконечно малых величин, то есть величин, стремящихся к 0. В следующих разделах на этой основе мы будем изучать свойства величин, имеющих произвольное значение предела.

Определение 2.9Функция называетсябесконечно малойвеличиной при базе , если её предел при данной базе равен 0, то есть .

Заметим, что в этом определении фигурирует фиксированная база ; в зависимости от того, какая именно база взята, одна и та же функция может как быть бесконечно малой, так и не быть ею.

Пример 2.8Рассмотрим функцию . При базе эта функция является бесконечно малой, а при базе -- не является.

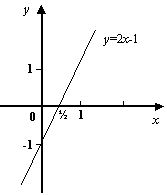
Рис.2.16.График функции

CLX.ru - реклама в интернет

Проверим это. Покажем, что . Возьмём произвольное и решим неравенство . Оно эквивалентно неравенству . Получаем ; это означает, что при , где , неравенство выполняется, то есть 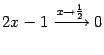. Мы показали, что -- бесконечно малая при .

Теперь покажем, что , то есть что эта величина не является бесконечно малой при . Возьмём и найдём окрестность точки 0, в которой выполняется неравенство . Это неравенство, очевидно, эквивалентно неравенству , то есть при попадание в -окрестность точки 0 гарантирует выполнение неравенства . Это означает, что .

Пример 2.9Функция 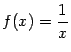-- бесконечно малая при , и при . Для того, чтобы это доказать, достаточно для любого указать окончание базы , на котором выполняется неравенство . При 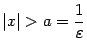, очевидно, неравенство выполняется. Это означает, что .

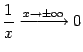Докажем теперь теорему, связывающую бесконечно малые с величинами, имеющими произвольное значение предела.

Теорема 2.4Функция имеет при базе предел, равный , тогда и только тогда, когда величина является бесконечно малой при базе :

Доказательство. Согласно определению предела, равенство означает, что для любого можно найти такое окончание , что

при всех

(2.1)

Условие означает, что для любого можно найти такое окончание , что

при всех

CLX.ru - реклама в интернет

Но это, очевидно, то же, что формула (2.1).

Теперь обратимся к свойствам, касающимся собственно бесконечно малых.

Теорема 2.5Пусть и -- бесконечно малые при одной и той же базе . Тогда и их сумма -- тоже бесконечно малая при базе .

Доказательство.Пусть фиксировано некоторое число . Рассмотрим положительное число . Условие означает, что найдётся такое окончание , на котором меньше этого положительного числа: при всех .

Точно так же, условие означает, что найдётся такое окончание , на котором при всех . По определению базы, она содержит некоторое окончание . Так как -- часть как , так и , то оба неравенства выполняются при . Тогда при будет

Итак, при произвольно заданном мы предъявили такое окончание , на котором выполняется неравенство . Это означает, что , то есть что -- бесконечно малая при базе .

Пример 2.10При базе рассмотрим две бесконечно малых величины: и 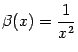. Вместе с ними и величина 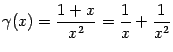тоже является бесконечно малой при базе .

Докажем теперь, как следствие из предыдущей теоремы, утверждение о том, что бесконечно малой является сумма не только двух, но любого числа бесконечно малых величин.

Следствие 2.1Пусть -- бесконечно малые при базе , . Тогда величина

также является бесконечно малой при базе .

Доказательство. Доказывать утверждение теоремы мы будем по индукции по числу слагаемых. Для двух слагаемых это утверждение верно по теореме 2.5. Пусть утверждение верно для слагаемых; это означает, что величина бесконечно мала. Покажем, что тогда оно верно и для слагаемых. По условию бесконечно мала также величина и, значит, по теореме 2.5 бесконечно мала сумма этих двух бесконечно малых . Тем самым шаг индукции сделан и утверждение доказано для произвольного числа слагаемых .

В дальнейшем нам часто будет нужно рассматривать функции, которые не превосходят некоторой постоянной на некотором окончании данной базы. Дадим им следующее название.

Определение 2.10Функция называетсялокально ограниченнойпри базе , если она определена на некотором окончании этой базы и существует такая постоянная , что при всех .

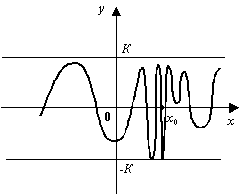
Рис.2.17.Локально ограниченная величина при базе

Пример 2.11Любая постоянная величина локально ограничена при любой базе. Действительно, в качестве ограничивающей постоянной достаточно взять ; тогда условие верно для из любого окончания любой базы .

Докажем следующее утверждение, имеющее вспомогательный характер для дальнейшего.

Предложение 2.1Пусть при данной базе две функции и являются локально ограниченными. Тогда и их произведение тоже локально ограничено при этой базе.

Доказательство. Из условия следует, что при и при , где -- некоторые постоянные и -- некоторые окончания базы . Возьмём окончание ; при будут выполнены оба неравенства и, следовательно,

Это означает, что постоянная служит ограничивающей постоянной для произведения на окончании , то есть это произведение локально ограничено при базе .

Локальная ограниченность функции не означает, что она ограничена на всей своей области определения. Например, функция локально ограничена при базе , но не является ограниченной функцией при всех . Если в качестве базы рассматривается , то локальная ограниченность функции при этой базе означает, что функция ограничена в некоторой, быть может, достаточно малой, окрестности точки.

Теорема 2.6Пусть функция имеет предел при базе . Тогда эта функция локально ограничена при этой базе.

Доказательство. Пусть ; это означает, что при любом (возьмём, например, ) найдётся такое окончание базы , что для любого . Тем самым, при выполнено двойное неравенство .

Выберем из двух чисел и число с большей абсолютной величиной и обозначим его : . Тогда, очевидно, из последнего неравенства следует, что ; это означает, что функция локально ограничена.

В частности, локально ограничены при базе все бесконечно малые при базе , так как все они, по определению, имеют предел (равный 0).

Пример 2.12Приведём пример, показывающий, что обратное к теореме 2.6 утверждение неверно, то есть что существуют функции, локально ограниченные при некоторой базе, однако не имеющие предела при этой базе. Рассмотрим функцию и базу . Локальная ограниченность функции очевидна: можно взять постоянную и окончание базы , тогда при всех . Однако не имеет предела при : какое бы окончание ни взять, при значения многократно изменяются от до 1 и назад и не приближаются ни к какому постоянному значению. (В качестве упражнения проведите строгое доказательство того, что предел не существует: докажите, что при нельзя указать окончания базы , при всех из которого при некотором выполнялось бы неравенство . Такое окончание должно было бы существовать по определению предела, если бы предел существовал.)

Поскольку предела при не существует, то если сделать замену , получится, что предел также не существует. График функции представлен на следующем рисунке.

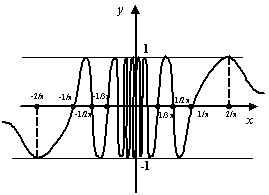
Рис.2.18.График

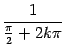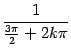График совершает бесконечно много колебаний при подходе к 0. Размах каждого колебания остаётся один и тот же, от до 1. Значения, равные 1, функция принимает в точках вида , , значения, равные ,-- в точках вида , , а значения, равные 0,-- в точках вида , .

Докажем теперь теорему о взаимосвязи локально ограниченных и бесконечно малых величин.

Теорема 2.7Пусть -- база, функция локально ограничена, а функция бесконечно мала при этой базе. Тогда их произведение -- бесконечно малая при базе .

Доказательство. Так как локально ограничена при базе , то при некотором и всех из некоторого окончания базы . Фиксируем произвольное число и рассмотрим положительное число . Так как -- бесконечно малая при базе , то найдётся такое окончание , что при всех выполняется неравенство . Рассмотрим теперь некоторое окончание . (Такое окончание существует по определению базы.) Так как -- часть как , так и , то при выполняются одновременно неравенства и , из которых следует, что при всех . Так как число было выбрано произвольно, это означает, что функция является бесконечно малой при базе .

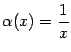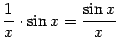Пример 2.13Пусть и . Так как бесконечно мала, а локально ограничена при базе , то их произведение -- бесконечно малая при , а также при и при (см.упражнение 2.4).

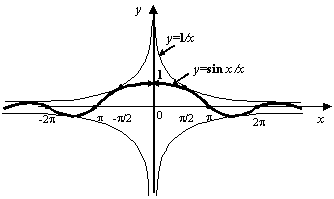
Рис.2.19.График

Пример 2.14В предыдущем примере сделаем замену . Тогда, очевидно, функция перейдёт в функцию , а базы , и , соответственно, в базы , и . Значение предела 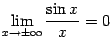при замене не изменится, так что

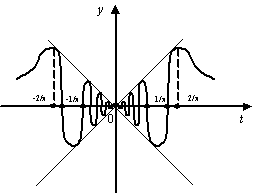
Рис.2.20.График функции

Следствие 2.2Пусть -- постоянная и -- бесконечно малая при базе . Тогда -- тоже бесконечно малая при базе .

Доказательство. Достаточно заметить, что локально ограничена при базе и сослаться на предыдущую теорему.

Следствие 2.3Пусть -- бесконечно малые при базе и -- произвольные постоянные. Тогда величина вида

является бесконечно малой при базе .

Доказательство. Чтобы доказать это следствие, достаточно заметить, что все слагаемые являются бесконечно малыми, согласно предыдущему следствию, а затем применить утверждение следствия 2.1.

Замечание 2.1Утверждение доказанного следствия, с алгебраической точки зрения, означает, что множество всех функций, определённых на некотором фиксированном окончании базы и бесконечно малых при этой базе , имеет структурулинейного пространства: любые элементы этого пространства можно умножать на постоянные и складывать, не выходя за рамки этого пространства.

Общие свойства пределов

В этом разделе мы на основе изученных выше свойств бесконечно малых величин (то есть функций, имеющих предел, равный 0) выясним свойства функций, имеющих произвольное значение предела.

Теорема 2.8Пусть функции и имеют пределы при одной и той же базе :

Тогда функция также имеет предел при базе , и этот предел равен сумме пределов слагаемых:

Доказательство. Равенство означает, в соответствии с теоремой 2.4, что величина -- бесконечно малая; равенство -- что -- бесконечно малая. Поэтому по теореме 2.5 сумма