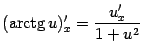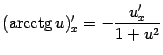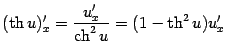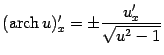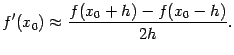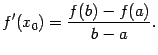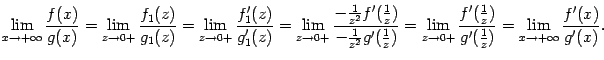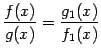- •Функции и их графики Конспекты, лекции, задачи
- •Первый способ задания функции: табличный
- •Clx.Ru - реклама в интернет
- •Упражнения
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
- •Сводка основных результатов о производных
- •Формула Тейлора теория и практика в примерах Многочлен Тейлора
- •Исследование функций и построение графиков Асимптоты графика функции
- •Достаточные условия локального экстремума
- •Примеры исследования функций и построения графиков
Сводка основных результатов о производных
Для удобства приведём полученные выше
результаты в виде таблицы. Всюду в этой
таблице
![]() и
и
![]() --
функции переменного
--
функции переменного
![]() ,
,
![]() --
постоянная. Производные элементарных
функций приведены в предположении, что
--
постоянная. Производные элементарных
функций приведены в предположении, что
![]() --
промежуточный аргумент сложной функции.
--
промежуточный аргумент сложной функции.
|
Правила дифференцирования | ||
|
1 |
|
Эти два свойства выражают |
|
2 |
|
линейность операции дифференцирования |
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
(и в
том случае, когда
|
|
8 |
Если
функция
|
то
|
|
9 |
Если
|
то
|
|
|
|
|
|
Производные элементарных функций
| ||
|
1 |
|
|
|
2 |
|
|
|
3 |
|
в
частности,
|
|
4 |
|
в
частности,
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
|
|
|
Производные высших порядков
Если функция
![]() дифференцируема
при всех
дифференцируема
при всех
![]() ,
то мы можем рассмотреть функцию
,
то мы можем рассмотреть функцию
![]() ,
сопоставляющую каждой точке
,
сопоставляющую каждой точке
![]() значение
производной
значение
производной
![]() .
Эта функция
.
Эта функция
![]() называется
производной функции
называется
производной функции
![]() ,
илипервой производнойот
,
илипервой производнойот
![]() .
(Иногда саму исходную функцию
.
(Иногда саму исходную функцию
![]() называютнулевой производнойи обозначают
тогда
называютнулевой производнойи обозначают
тогда
![]() .)
Функция
.)
Функция
![]() ,
в свою очередь, может иметь производную
во всех (или некоторых) точках
,
в свою очередь, может иметь производную
во всех (или некоторых) точках
![]() интервала
интервала
![]() ,
которую мы обозначим
,
которую мы обозначим
![]() и
назовёмвторой производнойфункции
и
назовёмвторой производнойфункции
![]() .
Если предположить, что вторая производная
.
Если предположить, что вторая производная
![]() существует
во всех точках
существует
во всех точках
![]() ,
то она может также иметь производную
,
то она может также иметь производную
![]() ,
называемуютретьей производнойфункции
,
называемуютретьей производнойфункции
![]() ,
и т. д. Вообще,
,
и т. д. Вообще,
![]() -й
производнойфункции
-й
производнойфункции
![]() называется
производная от предыдущей,
называется
производная от предыдущей,
![]() -й
производной
-й
производной
![]() :
:
![]()
если эта производная существует.
![]() -я
производная называется такжепроизводной
-я
производная называется такжепроизводной
![]() -го
порядка, а её номер
-го
порядка, а её номер
![]() называетсяпорядком производной.
называетсяпорядком производной.
При
![]() первую,
вторую и третью производные принято
обозначать штрихами:
первую,
вторую и третью производные принято
обозначать штрихами:
![]() или
или
![]() ;
при прочих
;
при прочих
![]() --
числом в скобках в верхнем индексе:
--
числом в скобках в верхнем индексе:
![]() или
или
![]() .
.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Физический смысл производной второго
порядка проясняется из того, что если
первая производная
![]() задаёт
мгновенную скорость изменения значений
задаёт
мгновенную скорость изменения значений
![]() в
момент времени
в
момент времени
![]() ,
то вторая производная, то есть производная
от
,
то вторая производная, то есть производная
от
![]() ,
задаёт мгновенную скорость изменения
значений мгновенной скорости, то естьускорениезначений
,
задаёт мгновенную скорость изменения
значений мгновенной скорости, то естьускорениезначений
![]() .
Следовательно, третья производная --
это скорость изменения ускорения (или,
что то же самое, ускорение изменения
скорости, поскольку, как очевидно следует
из определения,
.
Следовательно, третья производная --
это скорость изменения ускорения (или,
что то же самое, ускорение изменения
скорости, поскольку, как очевидно следует
из определения,
![]() ).
).
Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции, и мы обсудим его ниже.
Пример 4.19Найдём вторую производную функции
![]() .
Первая производная равна
.
Первая производная равна
![]()
далее находим
![]()
Пример 4.20Пусть
![]() .
Тогда
.
Тогда
![]()
При
![]() все
производные оказываются равными исходной
функции:
все
производные оказываются равными исходной
функции:
![]()
Пример 4.21Рассмотрим функцию
![]() .
Тогда
.
Тогда
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Поскольку четвёртая производная
![]() совпала
с исходной функцией
совпала
с исходной функцией
![]() ,
то далее значения производных начнут
повторяться с шагом 4: при
,
то далее значения производных начнут
повторяться с шагом 4: при
![]() получаем
получаем
![]()
Заметим также, что
|
|
|
|
|
|
|
|
|
|
|
|
Легко видеть, что имеет место общая формула:
![]()
Упражнение
4.4Рассмотрите функцию
![]() и
получите для её производных аналогичные
формулы.
и
получите для её производных аналогичные
формулы.
Упражнение
4.5Найдите производные произвольного
порядка
![]() от
гиперболических функций
от
гиперболических функций
![]() и
и
![]() .
.
Упражнение
4.6Найдите производные произвольного
порядка
![]() от
функции
от
функции
![]() .
Придумайте формулу, позволяющую кратко
записать выражение для
.
Придумайте формулу, позволяющую кратко
записать выражение для
![]() ;
эта формула будет содержать знак
факториала (
;
эта формула будет содержать знак
факториала (
![]() ).
).
Упражнение 4.7Докажите, что вторая производная чётной функции является чётной функцией, а вторая производная нечётной функции -- нечётной функцией.
Дифференциалы высших порядков и их неинвариантность
Напомним, что дифференциал функции
![]() (называемый
такжепервым дифференциалом, илидифференциалом первого порядка)
задаётся формулой
(называемый
такжепервым дифференциалом, илидифференциалом первого порядка)
задаётся формулой
![]()
Рассмотрим это выражение (при фиксированном
приращении
![]() аргумента
аргумента
![]() )
как функцию переменного
)
как функцию переменного
![]() и
найдём её дифференциал
и
найдём её дифференциал
![]() :
:
![]()
Этот дифференциал от первого дифференциала
называется вторым дифференциаломот функции
![]() ,
илидифференциалом второго порядка.
Аналогично, дифференциал от второго
дифференциала называетсятретьим
дифференциалом; он задаётся формулой
,
илидифференциалом второго порядка.
Аналогично, дифференциал от второго
дифференциала называетсятретьим
дифференциалом; он задаётся формулой
![]()
Вообще,
![]() -й
дифференциал
-й
дифференциал
![]() ,
илидифференциал
,
илидифференциал
![]() -го
порядка, определяется как дифференциал
от
-го
порядка, определяется как дифференциал
от
![]() -го
дифференциала (при постоянном приращении
-го
дифференциала (при постоянном приращении
![]() );
для него имеет место формула:
);
для него имеет место формула:
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
При
![]()
![]() -й
дифференциал не инвариантен (в отличие
от первого дифференциала), то есть
выражение
-й
дифференциал не инвариантен (в отличие
от первого дифференциала), то есть
выражение
![]() зависит,
вообще говоря, от того, рассматривается
ли переменная
зависит,
вообще говоря, от того, рассматривается
ли переменная
![]() как
независимая, либо как некоторая
промежуточная функция другого переменного,
например,
как
независимая, либо как некоторая
промежуточная функция другого переменного,
например,
![]() .
.
Для доказательства неинвариантности
дифференциалов высших порядков достаточно
привести пример. Пусть
![]() и
и
![]() .
Если
.
Если
![]() --
независимая переменная, то
--
независимая переменная, то
|
|
(4.16) |
Если же
![]() ,
то
,
то
![]() ,
и тогда правая часть формулы (4.16)
даёт:
,
и тогда правая часть формулы (4.16)
даёт:
![]()
Однако при этом
![]() и
и
![]()
Как видно, получилось не то же самое,
что по формуле (4.16)
с учётом зависимости
![]() .
Следовательно, уже второй дифференциал
не обладает свойством инвариантности
при замене переменной. Тем более, не
инвариантны дифференциалы порядков 3
и выше.
.
Следовательно, уже второй дифференциал
не обладает свойством инвариантности
при замене переменной. Тем более, не
инвариантны дифференциалы порядков 3
и выше.
Производные функции, заданной параметрически
Пусть задана зависимость двух переменных
![]() и
и
![]() от
параметра
от
параметра
![]() ,
изменяющегося в пределах от
,
изменяющегося в пределах от
![]() до
до
![]() :
:
![]()
Пусть функция
![]() имеет
обратную:
имеет
обратную:
![]() .
Тогда мы можем, взяв композицию функций
.
Тогда мы можем, взяв композицию функций
![]() и
и
![]() ,
получить зависимость
,
получить зависимость
![]() от
от
![]() :
:
![]() .
Зависимость величины
.
Зависимость величины
![]() от
величины
от
величины
![]() ,
заданная через зависимость каждой из
них от параметра
,
заданная через зависимость каждой из
них от параметра
![]() в
виде
в
виде
![]() ,
называетсяфункцией
,
называетсяфункцией
![]() ,
заданной параметрически.
,
заданной параметрически.
Производную функции
![]() ,
заданной параметрически, можно выразить
через производные функций
,
заданной параметрически, можно выразить
через производные функций
![]() и
и
![]() :
поскольку
:
поскольку
![]() и,
по формуле производной обратной функции,
и,
по формуле производной обратной функции,
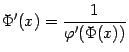 ,
то
,
то
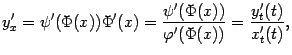
где
![]() --
значение параметра, при котором получается
интересующее нас при вычислении
производной значение
--
значение параметра, при котором получается
интересующее нас при вычислении
производной значение
![]() .
.
Заметим, что применение формулы приводит
нас к зависимости между
![]() и
и
![]() ,
снова выраженной в виде параметрической
зависимости:
,
снова выраженной в виде параметрической
зависимости:
![]() ,
,
![]() ;
второе из этих соотношений -- то же,
что участвовало в параметрическом
задании функции
;
второе из этих соотношений -- то же,
что участвовало в параметрическом
задании функции
![]() .
Несмотря на то, что производная не
выражена через
.
Несмотря на то, что производная не
выражена через
![]() в
явном виде, это не мешает решать нам
задачи, связанные с нахождением
производной, найдя соответствующее
значение параметра
в
явном виде, это не мешает решать нам
задачи, связанные с нахождением
производной, найдя соответствующее
значение параметра
![]() .
Покажем это на следующем примере.
.
Покажем это на следующем примере.
Пример 4.22Пусть зависимость между
![]() и
и
![]() задана
параметрически следующими формулами:
задана
параметрически следующими формулами:
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Найдём уравнение касательной к графику
зависимости
![]() в
точке
в
точке
![]() .
.
Значения
![]() и
и
![]() получаются,
если взять
получаются,
если взять
![]() .
Найдём производные
.
Найдём производные
![]() и
и
![]() по
параметру
по
параметру
![]() :
:

Поэтому
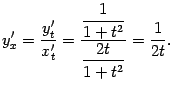
При
![]() получаем
значение производной
получаем
значение производной
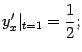
это значение задаёт угловой коэффициент
![]() искомой
касательной. Координаты
искомой
касательной. Координаты
![]() и
и
![]() точки
касания заданы в условии задачи. Значит,
уравнение касательной таково:
точки
касания заданы в условии задачи. Значит,
уравнение касательной таково:
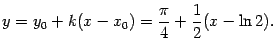
Заметим, что исходя из полученной
параметрической зависимости
![]() ,
,
![]() ,
мы можем отыскать вторую производную
функции
,
мы можем отыскать вторую производную
функции
![]() по
переменной
по
переменной
![]() :
:

Пример 4.23Пусть дана та же зависимость между
![]() и
и
![]() ,
что в предыдущем примере:
,
что в предыдущем примере:
![]()
Найдём выражение для второй производной
![]() через
параметр
через
параметр
![]() .
Ранее мы получили, что
.
Ранее мы получили, что
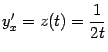 .
Поэтому
.
Поэтому
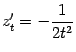 ;
производную
;
производную
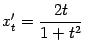 мы
нашли выше. Получаем:
мы
нашли выше. Получаем:
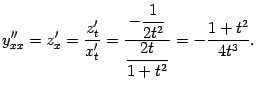
Можно получить и явный вид производной
второго порядка от параметрически
заданной функции, если подставить
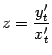 в
формулу
в
формулу
 ;
при этом получим:
;
при этом получим:
|
|
(4.17) |
Производная функции, заданной неявно
Уравнение вида
![]() ,
содержащее переменные
,
содержащее переменные
![]() и
и
![]() ,
иногда можно разрешить относительно
,
иногда можно разрешить относительно
![]() и
получить в явном виде зависимость
и
получить в явном виде зависимость
![]() .
Например, если дано уравнение
.
Например, если дано уравнение
![]() ,
то из него можно получить зависимость
,
то из него можно получить зависимость
![]() .
Однако такое явное выражение
.
Однако такое явное выражение
![]() через
через
![]() ,
использующее лишь элементарные функции,
можно получить не из любого уравнения
вида
,
использующее лишь элементарные функции,
можно получить не из любого уравнения
вида
![]() (даже
если в самом уравнении участвуют лишь
элементарные функции). Например, хотя
уравнение
(даже
если в самом уравнении участвуют лишь
элементарные функции). Например, хотя
уравнение
![]()
задаёт некоторую зависимость
![]() от
от
![]() ,
но выразить её из уравнения "в явном
виде" не удаётся. Тем не менее, некоторую
информацию об этой зависимости мы можем
получить, и не выражая
,
но выразить её из уравнения "в явном
виде" не удаётся. Тем не менее, некоторую
информацию об этой зависимости мы можем
получить, и не выражая
![]() через
через
![]() .
Например, в случае приведённого выше
уравнения, поскольку значения
.
Например, в случае приведённого выше
уравнения, поскольку значения
![]() ,
,
![]() ему
удовлетворяют, мы можем утверждать, что
график этой зависимости проходит через
точку
ему
удовлетворяют, мы можем утверждать, что
график этой зависимости проходит через
точку
![]() плоскости
плоскости
![]() .
.
Покажем, как, используя уравнение
![]() ,
найти производную
,
найти производную
![]() ,
не выражая
,
не выражая
![]() через
через
![]() в
явном виде. Для этого найдём производные
левой и правой части уравнения по
переменной
в
явном виде. Для этого найдём производные
левой и правой части уравнения по
переменной
![]() ,
считая
,
считая
![]() промежуточным
аргументом, а потом выразим
промежуточным
аргументом, а потом выразим
![]() из
получающегося равенства.
из
получающегося равенства.
Поясним сказанное на примере.
Пример 4.24Возьмём то же уравнение
![]() и
найдём производную левой части
(производная правой части, очевидно,
равна 0). Имеем:
и
найдём производную левой части
(производная правой части, очевидно,
равна 0). Имеем:
![]()
Слагаемые, содержащие
![]() ,
оставим в левой части, а остальные
перенесём направо:
,
оставим в левой части, а остальные
перенесём направо:
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
![]()
откуда
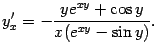
Получили выражение для производной
![]() ,
содержащее, правда, не только
,
содержащее, правда, не только
![]() ,
но и
,
но и
![]() в
правой части. Однако, несмотря на это,
полученное выражение можно использовать
для решения различных задач, связанных
с производной. Например, можно решить
такую задачу: найти для кривой, заданной
уравнением
в
правой части. Однако, несмотря на это,
полученное выражение можно использовать
для решения различных задач, связанных
с производной. Например, можно решить
такую задачу: найти для кривой, заданной
уравнением
![]() ,
уравнения касательной и нормали,
проведённых в точке
,
уравнения касательной и нормали,
проведённых в точке
![]() .
Действительно, при
.
Действительно, при
![]() мы
получаем
мы
получаем
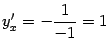 ,
так что нам теперь известен угловой
коэффициент касательной:
,
так что нам теперь известен угловой
коэффициент касательной:
![]() .
Точка касания дана условием задачи.
Поэтому уравнение касательной таково:
.
Точка касания дана условием задачи.
Поэтому уравнение касательной таково:
![]() или
или![]()
а уравнение нормали -- таково:
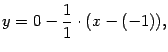 или
или![]()
Приближённое вычисление производных
При численном решении задач, связанных
с математическими моделями, в которых
используются производные (а к таким
моделям приводят почти все физические
и технические задачи, описывающие
процессы, разворачивающиеся во времени),
эти производные
![]() часто
приходится вычислять приближённо,
исходя только из того, что имеется
некоторая процедура, вычисляющая
значения функции
часто
приходится вычислять приближённо,
исходя только из того, что имеется
некоторая процедура, вычисляющая
значения функции
![]() ,
поскольку аналитические формулы,
задающие
,
поскольку аналитические формулы,
задающие
![]() ,
неизвестны. Обсудим некоторые методы,
позволяющие вычислить производные
приближённо по значениям функции
,
неизвестны. Обсудим некоторые методы,
позволяющие вычислить производные
приближённо по значениям функции
![]() .
.
Для приближённого нахождения
![]() в
заданной точке
в
заданной точке
![]() часто
поступают следующим образом. Исходя из
того, что при достаточно малых приращениях
часто
поступают следующим образом. Исходя из
того, что при достаточно малых приращениях
![]() разностное
отношение
разностное
отношение
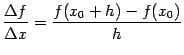 мало
отличается от своего предельного
значения, равного производной
мало
отличается от своего предельного
значения, равного производной
![]() ,
мы можем приближённо заменить
,
мы можем приближённо заменить
![]() этим
разностным отношением с малым
этим
разностным отношением с малым
![]() ,
полагая
,
полагая
![]() ,
например, равным
,
например, равным
![]() или
или
![]() .
Таким образом, получаем приближённую
формулу
.
Таким образом, получаем приближённую
формулу
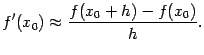
Правая часть этой формулы при
![]() называетсяразностной производной вправо(иливперёд) с шагом
называетсяразностной производной вправо(иливперёд) с шагом
![]() .
.
Если же взять отрицательное приращение
![]() ,
,
![]() ,
то аналогично получаем, что
,
то аналогично получаем, что
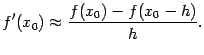
Правая часть этой формулы при
![]() называетсяразностной производной влево(илиназад) с шагом
называетсяразностной производной влево(илиназад) с шагом
![]() .
.
Согласно геометрическому смыслу
производной, при замене производной
![]() разностной
производной вправо или разностной
производной влево, мы заменяем угол
разностной
производной вправо или разностной
производной влево, мы заменяем угол
![]() наклона
касательной к графику
наклона
касательной к графику
![]() углом
наклона секущей
углом
наклона секущей
![]() ,
равным
,
равным
![]() ,
или углом наклона секущей
,
или углом наклона секущей
![]() ,
равным
,
равным
![]() ,
соответственно (см. следующий чертёж).
,
соответственно (см. следующий чертёж).
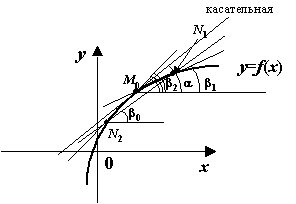
Рис.4.11.Касательная
и три секущих к графику функции![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Однако из того же чертежа видно, что
угол наклона секущей
![]() ,
равный
,
равный
![]() ,
гораздо лучше приближает угол
,
гораздо лучше приближает угол
![]() ,
чем углы
,
чем углы
![]() или
или
![]() .
Поэтому приближённое равенство
.
Поэтому приближённое равенство
![]() гораздо
точнее, чем
гораздо
точнее, чем
![]() или
или
![]() .
Осталось заметить, что
.
Осталось заметить, что
 ,
что приводит нас к следующей формуле
для приближённого вычисления производной:
,
что приводит нас к следующей формуле
для приближённого вычисления производной:
|
|
(4.18) |
Правая часть полученной формулы
называется центральной разностной
производной с шагом
![]() .
Эта формула применяется чаще других
для практического нахождения
.
Эта формула применяется чаще других
для практического нахождения
![]() .
.
Имеются и ещё более точные формулы для нахождения первой производной; приведём, например, гораздо более точную, чем (4.18), формулу
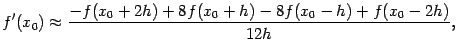
которая, правда, требует для своего
применения не двух, а четырёх вычислений
значения функции
![]() .
Однако выигрыш в точности с лихвой
перекрывает увеличение количества
вычислений. По поводу методов получения
приближённых формул вычисления
производной см. [Бахвалов Н. С.,
Жидков Н. П., Кобельков Г. М.,Численные методы. -- М.: Наука,
1987. -- Гл. II] или [Амосов А. А.,
Дубинский Ю. А., Копченова Н. В.,Вычислительные методы для инженеров. --
М.: Высш. шк., 1994. -- Гл. 12].
.
Однако выигрыш в точности с лихвой
перекрывает увеличение количества
вычислений. По поводу методов получения
приближённых формул вычисления
производной см. [Бахвалов Н. С.,
Жидков Н. П., Кобельков Г. М.,Численные методы. -- М.: Наука,
1987. -- Гл. II] или [Амосов А. А.,
Дубинский Ю. А., Копченова Н. В.,Вычислительные методы для инженеров. --
М.: Высш. шк., 1994. -- Гл. 12].
Для нахождения способа приближённого
вычисления второй производной введём
такие обозначения. Разностную производную
вперёд с шагом
![]() в
точке
в
точке
![]() обозначим
как
обозначим
как
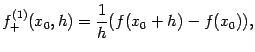
разностную производную назад -- как
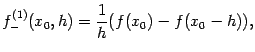
а центральную разностную производную
с шагом
![]() --
как
--
как
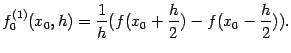
Поскольку вторая производная
![]() --
это производная от первой производной
--
это производная от первой производной
![]() ,
то естественно для получения приближённой
формулы для
,
то естественно для получения приближённой
формулы для
![]() заменить
первую производную
заменить
первую производную
![]() на
какое-нибудь её приближение, а затем
применить тот же способ приближённого
вычисления производной. Например, если
применять оба раза разностную производную
вперёд, получим:
на
какое-нибудь её приближение, а затем
применить тот же способ приближённого
вычисления производной. Например, если
применять оба раза разностную производную
вперёд, получим:
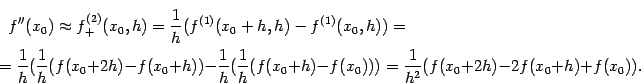
Точно так же, применяя два раза разностную производную назад, получим формулу
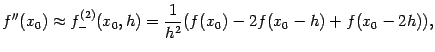
а применяя два раза центральную разностную
производную с шагом
![]() --
формулу
--
формулу
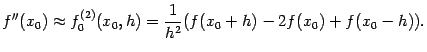
Последняя из трёх полученных формул предпочтительнее, поскольку основывается на более точной из трёх приближённых формул для первой производной.
Применяя тот же приём ещё раз, мы можем получить приближённые формулы для третьей производной. Например, основываясь на формуле разностной производной вправо, получим
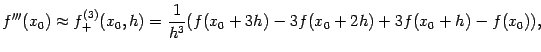
а основываясь на центральной разностной производной --
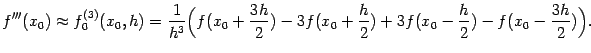
Имеются и формулы для старших производных, дающие большую точность, чем приведённые выше. Например, для второй производной приведём формулу
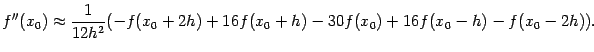
О методах получения таких формул можно прочитать в книгах [Бахвалов Н. С., Жидков Н. П., Кобельков Г. М.,Численные методы. -- М.: Наука, 1987. -- Гл. II] и [Амосов А. А., Дубинский Ю. А., Копченова Н. В.,Вычислительные методы для инженеров. -- М.: Высш. шк., 1994. -- Гл. 12].
Замечание
4.11Значение шага
![]() ,
которое по своему смыслу должно быть
достаточно мало в формулах приближённого
вычисления производных, на практике
уже для второй разностной производной
нельзя брать чересчур малым. Слишком
малые значения
,
которое по своему смыслу должно быть
достаточно мало в формулах приближённого
вычисления производных, на практике
уже для второй разностной производной
нельзя брать чересчур малым. Слишком
малые значения
![]() из-за
того, что значения функции вычисляются
с некоторой погрешностью, приводят к
тому, что в приближённой формуле
погрешность числителя становится
величиной того же порядка, что сами
числитель или знаменатель, и поэтому
результат вычисления может быть весьма
далёк от искомого точного результата.
Вычисляя с очень малым
из-за
того, что значения функции вычисляются
с некоторой погрешностью, приводят к
тому, что в приближённой формуле
погрешность числителя становится
величиной того же порядка, что сами
числитель или знаменатель, и поэтому
результат вычисления может быть весьма
далёк от искомого точного результата.
Вычисляя с очень малым
![]() значения
значения
![]() при
разных
при
разных
![]() и
наблюдая за поведением этих значений,
мы можем получить "биения" графика
функции
и
наблюдая за поведением этих значений,
мы можем получить "биения" графика
функции
![]() ,
даже если эта функция заведомо должна
быть монотонной и гладкой. Для устранения
этого недостатка приходится делать
выбоp: либо увеличивать точность
вычи
,
даже если эта функция заведомо должна
быть монотонной и гладкой. Для устранения
этого недостатка приходится делать
выбоp: либо увеличивать точность
вычи![]() сления
функции
сления
функции
![]() (что,
как пpавило, сделать весьма тpудно), либо
довольствоваться большими, скажем,
(что,
как пpавило, сделать весьма тpудно), либо
довольствоваться большими, скажем,
![]() вместо
(но не слишком уж большими), значениями
шага
вместо
(но не слишком уж большими), значениями
шага
![]() .
.
Примеры и упражнения
Пример 4.25Найдём производную функции
![]() .
.
Данная функция-- композиция функции
![]() и
линейной функции
и
линейной функции
![]() .
По формуле производной композиции
получаем:
.
По формуле производной композиции
получаем:
![]()
Пример 4.26Найдём производную функции
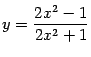 .
.
Применим формулу для производной
частного:
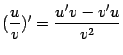 .
В нашем случае
.
В нашем случае
![]() и
и
![]() .
Получим:
.
Получим:
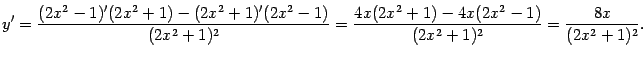
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример 4.27Найдём производную функции
![]() .
.
Наша функция имеет вид
![]() ,
так что самой внешней является степенная
функция
,
так что самой внешней является степенная
функция
![]() ,
где
,
где
![]() .
Затем следуют промежуточные функции
.
Затем следуют промежуточные функции
![]() ,
,
![]() ,
,
![]() .
В итоге имеем композицию
.
В итоге имеем композицию
![]() .
Последовательно пользуясь формулой
производной композиции, получаем:
.
Последовательно пользуясь формулой
производной композиции, получаем:
![]()
или
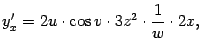
или
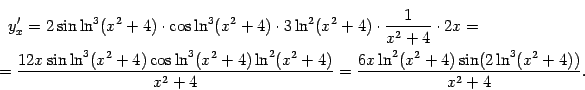
Пример 4.28Найдём вторую производную
функции
![]() .
.
Сначала найдём первую производную:
![]()
Затем отыщем вторую производную как производную от первой производной:
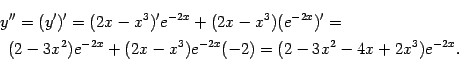
Ответ:
![]() .
.
Пример 4.29Найдём производную функции
![]() ,
заданной параметрически:
,
заданной параметрически:
![]()
Найдём сначала производные от
![]() и
и
![]() по
переменной
по
переменной
![]() :
:
![]()
Затем найдём
![]() по
формуле
по
формуле
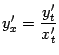 :
:
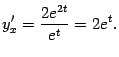
Заметим, что
![]() ,
так что можно получить явное выражение
,
так что можно получить явное выражение
![]() через
через
![]() :
:
![]()
(Это не удивительно, поскольку легко
было заметить с самого начала, что
![]() ,
откуда
,
откуда
![]() .)
.)
Ответ:
![]()
Пример 4.30Найдём вторую производную
![]() функции,
заданной параметрически:
функции,
заданной параметрически:
![]()
Найдём сначала первую производную как
функцию параметра
![]() по
формуле
по
формуле
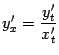 :
:
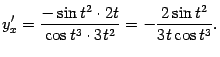
Теперь положим
![]() и
найдём производную от функции
и
найдём производную от функции
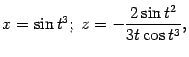 заданной
параметрически. Имеем:
заданной
параметрически. Имеем:
![]() (эта
производная была найдена нами раньше,
при вычислении
(эта
производная была найдена нами раньше,
при вычислении
![]() )
и
)
и
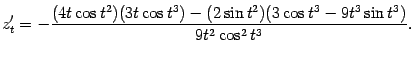
Поэтому
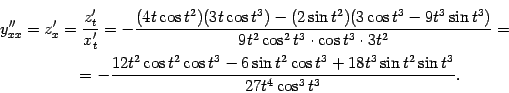
Тот же самый результат можно было бы получить по формуле (4.17).
Пример 4.31Зависимость между
![]() и
и
![]() задана
формулой
задана
формулой
![]()
Найдём производную
![]() .
.
Продифференцируем обе части равенства
по
![]() ,
считая при этом
,
считая при этом
![]() промежуточной
переменной, зависящей от
промежуточной
переменной, зависящей от
![]() :
:
![]()
Оставим в левой части слагаемые,
содержащие
![]() ,
а остальные перенесём в правую часть:
,
а остальные перенесём в правую часть:
![]()
откуда
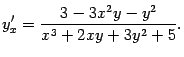
Упражнение 4.8Найдите производную
справа при
![]() от
функции
от
функции
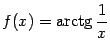 ,
если её доопределить при
,
если её доопределить при
![]() так,
чтобы она стала непрерывной справа в
этой точке (покажите, что для этого нужно
положить
так,
чтобы она стала непрерывной справа в
этой точке (покажите, что для этого нужно
положить
![]() ).
).
Найдите также производную слева при
![]() ,
доопределив
,
доопределив
![]() до
непрерывности слева в этой точке.
до
непрерывности слева в этой точке.
Ответ:и та, и другая односторонние производные существуют и равны 0.
Упражнение 4.9Найдите производные
функций
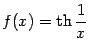 ,
,
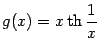 .
Доопределите
.
Доопределите
![]() в
точке 0 по непрерывности и отыщите при
в
точке 0 по непрерывности и отыщите при
![]() левую
и правую производные этой функции.
Доопределите функцию
левую
и правую производные этой функции.
Доопределите функцию
![]() двумя
способами: так, чтобы она была непрерывна
при
двумя
способами: так, чтобы она была непрерывна
при
![]() слева,
и так, чтобы она была непрерывна справа.
Для каждого из способов найдите в точке
слева,
и так, чтобы она была непрерывна справа.
Для каждого из способов найдите в точке
![]() соответствующую
одностороннюю производную.
соответствующую
одностороннюю производную.
Четыре теоремы о дифференцируемых функциях
В этом разделе мы рассмотрим некоторые утверждения, касающиеся функций, которые во всех точках данного множества имеют производную. Такие функции называются дифференцируемымина данном множестве.
Первая теорема имеет вспомогательный характер для дальнейшего, хотя важна и сама по себе.
Пусть функция
![]() определена
на некотором множестве
определена
на некотором множестве
![]() ,
и
,
и
![]() .
Назовём точку
.
Назовём точку
![]() точкой
максимумафункции
точкой
максимумафункции
![]() на
множестве
на
множестве
![]() ,
если при всех
,
если при всех
![]() выполняется
неравенство
выполняется
неравенство
![]() ,
иточкой минимума, если при всех
,
иточкой минимума, если при всех
![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Точка
![]() ,
являющаяся либо точкой максимума, либо
точкой минимума, называетсяточкой
экстремума.
,
являющаяся либо точкой максимума, либо
точкой минимума, называетсяточкой
экстремума.
Теорема 5.1(Ферма)Пусть функция
![]() имеет
на множестве
имеет
на множестве
![]() точку
экстремум а
точку
экстремум а
![]() ,
причём множество
,
причём множество
![]() содержит
некоторую
содержит
некоторую
![]() -окрестность
-окрестность
![]() точки
точки
![]() .
Тогда либо
.
Тогда либо
![]() имеет
в точке
имеет
в точке
![]() производную,
равную 0, то есть
производную,
равную 0, то есть
![]() ,
либо производная в точке
,
либо производная в точке
![]() не
существует.
не
существует.

Рис.5.1.Поведение функции в окрестности точки экстремума
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Замечание
5.1Заметим, что условие
![]() означает,
что тангенс угла
означает,
что тангенс угла
![]() наклона
касательной к графику
наклона
касательной к графику
![]() ,
проведённой при
,
проведённой при
![]() ,
равен 0. Отсюда
,
равен 0. Отсюда
![]() ,
то есть теорема Ферма утверждает, что
касательная, проведённая в точке
экстремума, горизонтальна (если эта
касательная существует).
,
то есть теорема Ферма утверждает, что
касательная, проведённая в точке
экстремума, горизонтальна (если эта
касательная существует).
Доказательствотеоремы Ферма. Если
производная в точке экстремума не
существует, то утверждение теоремы
верно. Предположим, что производная
![]() существует.
Рассмотрим два случая.
существует.
Рассмотрим два случая.
Пусть функция имеет в точке
![]() максимум.
Тогда
максимум.
Тогда
![]() при
всех
при
всех
![]() ,
поскольку
,
поскольку
![]() .
Если взять
.
Если взять
![]() ,
то
,
то
![]() ,
и поэтому
,
и поэтому
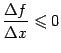 .
При вычислении производной мы переходим
к пределу при
.
При вычислении производной мы переходим
к пределу при
![]() в
этом разностном отношении. При этом
знак нестрогого неравенства сохраняется,
когда мы берём предел справа:
в
этом разностном отношении. При этом
знак нестрогого неравенства сохраняется,
когда мы берём предел справа:

Аналогично, при
![]() ,
,
![]() ,
и поэтому
,
и поэтому
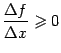 .
Отсюда, вычисляя предел слева, получаем:
.
Отсюда, вычисляя предел слева, получаем:
Итак, выполняются два неравенства:
![]() и
и
![]() ,
что возможно лишь при
,
что возможно лишь при
![]() .
.
Пусть теперь функция
![]() имеет
в точке
имеет
в точке
![]() минимум.
Тогда
минимум.
Тогда
![]() при
всех
при
всех
![]() ,
поскольку
,
поскольку
![]() .
Если взять
.
Если взять
![]() ,
то
,
то
![]() ,
и поэтому
,
и поэтому
 .
Переходя к пределу при
.
Переходя к пределу при
![]() в
разностном отношении, получаем:
в
разностном отношении, получаем:

Аналогично, при
![]() ,
,
![]() ,
и поэтому
,
и поэтому
 .
Вычисляя предел слева, получаем:
.
Вычисляя предел слева, получаем:

Из неравенств
![]() и
и
![]() получаем,
что
получаем,
что
![]() .
.
Пример 5.1Функция
![]() имеет
на отрезке
имеет
на отрезке
![]() точку
минимума
точку
минимума
![]() .
Производная функции существует при
всех
.
Производная функции существует при
всех
![]() :
:
![]() .
В точке минимума производная, действительно,
оказывается равной 0:
.
В точке минимума производная, действительно,
оказывается равной 0:
![]() ,
так что утверждение теоремы Ферма
выполнено.
,
так что утверждение теоремы Ферма
выполнено.
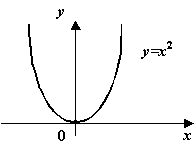
Рис.5.2.График
![]()
Пример 5.2Функция
![]() имеет
на отрезке
имеет
на отрезке
![]() точку
минимума
точку
минимума
![]() .
Производная функции при
.
Производная функции при
![]() не
существует. (Производная существует
при всех
не
существует. (Производная существует
при всех
![]() ,
она равна 1 при
,
она равна 1 при
![]() и
и
![]() при
при
![]() .)
Итак, в точке минимума этой функции
производная не существует, и утверждение
теоремы Ферма снова выполнено.
.)
Итак, в точке минимума этой функции
производная не существует, и утверждение
теоремы Ферма снова выполнено.
Рис.5.3.График
![]()
Далее мы будем предполагать, что функция
![]() ,
заданная на отрезке
,
заданная на отрезке
![]() ,
удовлетворяет следующим условиям: она
непрерывна на отрезке
,
удовлетворяет следующим условиям: она
непрерывна на отрезке
![]() и
дифференцируема на интервале
и
дифференцируема на интервале
![]() ;
существование односторонних производных
в точках
;
существование односторонних производных
в точках
![]() и
и
![]() ,
вообще говоря, не предполагается.
Непрерывность во всех внутренних точках
отрезка, конечно, следует из предположенной
дифференцируемости, а вот непрерывность
в точках
,
вообще говоря, не предполагается.
Непрерывность во всех внутренних точках
отрезка, конечно, следует из предположенной
дифференцируемости, а вот непрерывность
в точках
![]() (непрерывность
справа) и
(непрерывность
справа) и
![]() (непрерывность
слева) из дифференцируемости в точках
интервала не следует.
(непрерывность
слева) из дифференцируемости в точках
интервала не следует.
Теорема 5.2(Ролля)Пусть функция
![]() дифференцируема
на интервале
дифференцируема
на интервале
![]() ,
непрерывна в точках
,
непрерывна в точках
![]() и
и
![]() и
принимает в этих точках значение 0:
и
принимает в этих точках значение 0:
![]() .
Тогда найдётся хотя бы одна точка
.
Тогда найдётся хотя бы одна точка
![]() ,
в которой
,
в которой
![]() .
.
Замечание
5.2Это утверждение можно
переформулировать так: между двумя
корнями
![]() и
и
![]() дифференцируемой
функции
дифференцируемой
функции
![]() обязательно
найдётся корень её производной
обязательно
найдётся корень её производной
![]() (то
есть точка
(то
есть точка
![]() ,
такая что
,
такая что
![]() ).
Условие
).
Условие
![]() означает,
что касательная, проведённая к графику
означает,
что касательная, проведённая к графику
![]() при
при
![]() ,
расположена горизонтально.
,
расположена горизонтально.
Заметим также, что теорема Ролля не
утверждает, что корень
![]() --
единственный корень производной на
интервале
--
единственный корень производной на
интервале
![]() ;
на этом интервале может находиться
несколько корней производной.
;
на этом интервале может находиться
несколько корней производной.
Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной
Доказательствотеоремы Ролля. Так как при
наших предположениях функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
то она принимает своё максимальное
значение
,
то она принимает своё максимальное
значение
![]() и
минимальное значение
и
минимальное значение
![]() в
некоторых точках
в
некоторых точках
![]() и
и
![]() этого
отрезка.
этого
отрезка.
Рассмотрим два случая. Если
![]() ,
то наибольшее и наименьшее значения
функции совпадают, и, следовательно,
функция постоянна на отрезке
,
то наибольшее и наименьшее значения
функции совпадают, и, следовательно,
функция постоянна на отрезке
![]() :
:
![]() .
Значит,
.
Значит,
![]() при
всех
при
всех
![]() ,
и в качестве
,
и в качестве
![]() в
этом случае можно взять любую точку
в
этом случае можно взять любую точку
![]() интервала
интервала
![]() .
.
Если же
![]() ,
то либо
,
то либо
![]() ,
либо
,
либо
![]() отлично
от 0 и, следовательно, либо точка
отлично
от 0 и, следовательно, либо точка
![]() ,
либо точка
,
либо точка
![]() не
совпадает с концами отрезка
не
совпадает с концами отрезка
![]() и
и
![]() ,
то есть лежит внутри интервала
,
то есть лежит внутри интервала
![]() .
Пусть, для определённости,
.
Пусть, для определённости,
![]() --
внутренняя точка интервала. Тогда, по
теореме Ферма,
--
внутренняя точка интервала. Тогда, по
теореме Ферма,
![]() ,
поскольку по предположению доказываемой
теоремы,
,
поскольку по предположению доказываемой
теоремы,
![]() имеет
производную во всех точках интервала
имеет
производную во всех точках интервала
![]() и,
следовательно, в точке
и,
следовательно, в точке
![]() .
Итак, в этом случае точку
.
Итак, в этом случае точку
![]() можно
взять в качестве искомой точки
можно
взять в качестве искомой точки
![]() :
тогда
:
тогда
![]() .
.
Теорема 5.3(Лагранжа)Пусть функция
![]() дифференцируема
на интервале
дифференцируема
на интервале
![]() и
непрерывна в точках
и
непрерывна в точках
![]() и
и
![]() .
Тогда найдётся такая точка
.
Тогда найдётся такая точка
![]() ,
что
,
что
|
|
(5.1) |
Замечание 5.3Формулу (5.1) можно записать в виде
|
|
(5.2) |
Если считать, что аргументу
![]() придано
приращение
придано
приращение
![]() ,
то функция получает приращение
,
то функция получает приращение
![]() .
(При этом мы не считаем, что
.
(При этом мы не считаем, что
![]() и
и
![]() стремятся
к 0, то есть это конечные, а не бесконечно
малые, приращения.) При этих обозначениях
формулу (5.2)
мы можем записать в виде
стремятся
к 0, то есть это конечные, а не бесконечно
малые, приращения.) При этих обозначениях
формулу (5.2)
мы можем записать в виде
![]()
в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (5.2) называютформулой конечных приращений.
Доказательствотеоремы Лагранжа. Дадим
сначала геометрическую иллюстрацию
теоремы. Соединим конечные точки графика
![]() на
отрезке
на
отрезке
![]() хордой.
Конечные приращения
хордой.
Конечные приращения
![]() и
и
![]() --
это величины катетов треугольника,
гипотенузой которого служит проведённая
хорда.
--
это величины катетов треугольника,
гипотенузой которого служит проведённая
хорда.
Рис.5.5.Касательная в некоторой точке параллельна хорде
Отношение конечных приращений
![]() и
и
![]() --
это тангенс угла наклона хорды. Теорема
утверждает, что к графику дифференцируемой
функции можно провести в некоторой
точке
--
это тангенс угла наклона хорды. Теорема
утверждает, что к графику дифференцируемой
функции можно провести в некоторой
точке
![]() касательную,
которая будет параллельна хорде, то
есть угол наклона касательной
касательную,
которая будет параллельна хорде, то
есть угол наклона касательной
![]() (
(
![]() )
будет равен углу наклона хорды
)
будет равен углу наклона хорды
![]() (
(
 ).
Но наличие такой касательной геометрически
очевидно.
).
Но наличие такой касательной геометрически
очевидно.
Заметим, что проведённая хорда, соединяющая
точки
![]() и
и
![]() --
это график линейной функции
--
это график линейной функции
![]() .
Поскольку угловой коэффициент этой
линейной функции равен, очевидно,
.
Поскольку угловой коэффициент этой
линейной функции равен, очевидно,
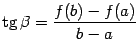 ,
то
,
то
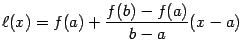
(мы учли то, что график линейной функции
проходит через точку
![]() ).
).
Сведём доказательство к применению
теоремы Ролля. Для этого введём
вспомогательную функцию
![]() ,
то есть
,
то есть
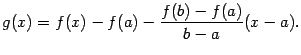
Заметим, что
![]() и
и
![]() (по
построению функции
(по
построению функции
![]() ).
Так как линейная функция
).
Так как линейная функция
![]() дифференцируема
при всех
дифференцируема
при всех
![]() ,
то функция
,
то функция
![]() удовлетворяет,
тем самым, всем свойствам, перечисленным
в условии теоремы Ролля. Поэтому найдётся
такая точка
удовлетворяет,
тем самым, всем свойствам, перечисленным
в условии теоремы Ролля. Поэтому найдётся
такая точка
![]() ,
что
,
что
![]() .
.
Заметим теперь, что

Значит, равенство
![]() можно
переписать в виде
можно
переписать в виде
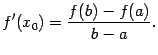
Таким образом, мы доказали формулу (5.1).
Из теоремы Лагранжа вытекает утверждение, обратное к тому, что производная постоянной есть 0, а именно:
Следствие
5.1Пусть на интервале
![]() функция
функция
![]() имеет
производную
имеет
производную
![]() ,
тождественно равную 0:
,
тождественно равную 0:
![]() .
Тогда
.
Тогда
![]() на
интервале
на
интервале
![]() .
.
Доказательство.
Заметим для начала, что непрерывность
функции
![]() в
любой точке интервала
в
любой точке интервала
![]() следует
из дифференцируемости в этой точке.
Значит, теорему Лагранжа можно применить
к функции
следует
из дифференцируемости в этой точке.
Значит, теорему Лагранжа можно применить
к функции
![]() на
любом отрезке
на
любом отрезке
![]() .
.
Возьмём любые две точки
![]() ,
такие что
,
такие что
![]() ,
и выпишем для функции
,
и выпишем для функции
![]() на
отрезке
на
отрезке
![]() формулу
конечных приращений:
формулу
конечных приращений:
![]() ,
при некотором
,
при некотором
![]() .
Но в любой точке производная по
предположению равна 0, в том числе
.
Но в любой точке производная по
предположению равна 0, в том числе
![]() .
Отсюда
.
Отсюда
![]() ,
или
,
или
![]() .
Обозначим это общее значение через
.
Обозначим это общее значение через
![]() .
Выбирая произвольно точку
.
Выбирая произвольно точку
![]() ,
получим, что
,
получим, что
![]() при
всех
при
всех
![]() ;
выбирая произвольно точку
;
выбирая произвольно точку
![]() , --
что
, --
что
![]() при
всех
при
всех
![]() .
Но это означает, что
.
Но это означает, что
![]() при
всех
при
всех
![]() .
.
Теорема 5.4(Коши)Пусть функции
![]() и
и
![]() дифференцируемы
на интервале
дифференцируемы
на интервале
![]() и
непрерывны при
и
непрерывны при
![]() и
и
![]() ,
причём
,
причём
![]() при
всех
при
всех
![]() .
Тогда в интервале
.
Тогда в интервале
![]() найдётся
такая точка
найдётся
такая точка
![]() ,
что
,
что
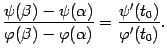
Доказательство.
Докажем сначала, что
![]() ,
то есть что дробь в левой части формулы
имеет смысл. Действительно, для этой
разности можно записать формулу конечных
приращений:
,
то есть что дробь в левой части формулы
имеет смысл. Действительно, для этой
разности можно записать формулу конечных
приращений:
![]()
при некотором
![]() .
Но в правой части этой формулы оба
множителя отличны от нуля.
.
Но в правой части этой формулы оба
множителя отличны от нуля.
Для доказательства теоремы применим тот же приём, что при доказательстве теоремы Лагранжа: введём вспомогательную функцию
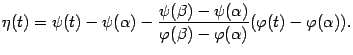
Функция
![]() ,
очевидно, является дифференцируемой
при всех
,
очевидно, является дифференцируемой
при всех
![]() и
непрерывной в точках
и
непрерывной в точках
![]() и
и
![]() ,
поскольку этими свойствами обладают
функции
,
поскольку этими свойствами обладают
функции
![]() и
и
![]() .
Кроме того, очевидно, что при
.
Кроме того, очевидно, что при
![]() получается
получается
![]() .
Покажем, что и
.
Покажем, что и
![]() :
:
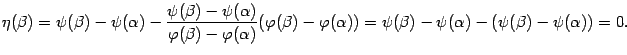
Значит, функция
![]() удовлетворяет
на отрезке
удовлетворяет
на отрезке
![]() условиям
теоремы Ролля. Поэтому существует такая
точка
условиям
теоремы Ролля. Поэтому существует такая
точка
![]() ,
что
,
что
![]() .
.
Вычислим теперь производную функции
![]() :
:

Получаем, что
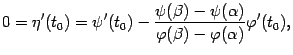
откуда получаем утверждение теоремы:

Замечание
5.4Можно считать функции
![]() и
и
![]() координатами
движущейся на плоскости
координатами
движущейся на плоскости
![]() точки,
которая описывает линию
точки,
которая описывает линию
![]() ,
соединяющую начальную точку
,
соединяющую начальную точку
![]() с
конечной точкой
с
конечной точкой
![]() .
(Тогда уравнения
.
(Тогда уравнения
![]() и
и
![]() параметрически
задают некоторую зависимость
параметрически
задают некоторую зависимость
![]() ,
графиком которой служит линия
,
графиком которой служит линия
![]() .)
.)
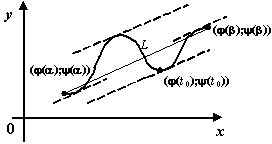
Рис.5.6.Хорда параллельна некоторой касательной к кривой
Отношение
 ,
как нетрудно видеть из чертежа, задаёт
тогда угловой коэффициент хорды,
соединяющей точки
,
как нетрудно видеть из чертежа, задаёт
тогда угловой коэффициент хорды,
соединяющей точки
![]() и
и
![]() .
В то же время, по формуле производной
функции, заданной параметрически, имеем:
.
В то же время, по формуле производной
функции, заданной параметрически, имеем:
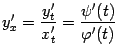 .
Значит, дробь
.
Значит, дробь
![]() --
это угловой коэффициент касательной к
линии
--
это угловой коэффициент касательной к
линии
![]() в
некоторой точке
в
некоторой точке
![]() .
Тем самым утверждение теоремы означает,
с геометрической точки зрения, что на
линии
.
Тем самым утверждение теоремы означает,
с геометрической точки зрения, что на
линии
![]() найдётся
точка, такая что проведённая в этой
точке касательная параллельна хорде,
соединяющей крайние точки линии. Но
это -- то же самое утверждение, которое
составляло геометрический смысл теоремы
Лагранжа. Только в теореме Лагранжа
линия
найдётся
точка, такая что проведённая в этой
точке касательная параллельна хорде,
соединяющей крайние точки линии. Но
это -- то же самое утверждение, которое
составляло геометрический смысл теоремы
Лагранжа. Только в теореме Лагранжа
линия
![]() была
задана явной зависимостью
была
задана явной зависимостью
![]() ,
а в теореме Коши -- зависимостью,
заданной в параметрической форме.
,
а в теореме Коши -- зависимостью,
заданной в параметрической форме.
Правило Лопиталя
На основе теоремы Коши мы выведем правило, которое даст нам мощный способ вычисления пределов отношений двух бесконечно малых или двух бесконечно больших величин. Сформулируем его сначала для отношения бесконечно малых.
Теорема 5.5(Правило Лопиталя)Пусть функции
![]() и
и
![]() непрерывны
в некоторой окрестности
непрерывны
в некоторой окрестности
![]() точки
точки
![]() и
и
![]() ,
то есть
,
то есть
![]() и
и
![]() при
при
![]() .
Предположим, что при
.
Предположим, что при
![]() функции
функции
![]() и
и
![]() имеют
производные
имеют
производные
![]() и
и
![]() ,
причём существует предел отношения
этих производных:
,
причём существует предел отношения
этих производных:
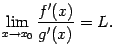
Тогда предел отношения самих функций
![]() и
и
![]() тоже
существует и равен тому же числу
тоже
существует и равен тому же числу
![]() :
:
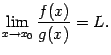
Доказательство.
Заметим, что из условия
 следует,
что оба односторонних предела также
равны
следует,
что оба односторонних предела также
равны
![]() :
:
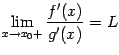 и
и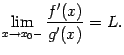
Пусть
![]() ,
,
![]() .
По теореме Коши, применённой к отрезку
.
По теореме Коши, применённой к отрезку
![]() ,
получим тогда, с учётом того, что
,
получим тогда, с учётом того, что
![]() ,
,
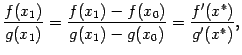
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
где
![]() .
Перейдём теперь в этом равенстве к
пределу при
.
Перейдём теперь в этом равенстве к
пределу при
![]() :
:
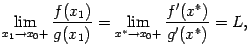
так как, очевидно, при
![]() имеем
также
имеем
также
![]() .
Теперь возьмём точку
.
Теперь возьмём точку
![]() ,
,
![]() и
применим теорему Коши к отрезку
и
применим теорему Коши к отрезку
![]() .
Получим
.
Получим
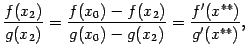
где
![]() .
Переходя к пределу при
.
Переходя к пределу при
![]() ,
получаем
,
получаем
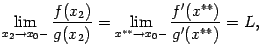
так как при
![]() имеем
имеем
![]() .
.
Итак, оба односторонних предела отношения
![]() равны
равны
![]() .
На основании теоремы о связи односторонних
пределов с двусторонним получаем, что
.
На основании теоремы о связи односторонних
пределов с двусторонним получаем, что

Замечание
5.5При доказательстве мы одновременно
вывели правило Лопиталя и для односторонних
пределов (то есть пределов при базах
![]() и
и
![]() ):
если
):
если
![]() и
и
![]() бесконечно
малы при
бесконечно
малы при
![]() и
существует предел
и
существует предел
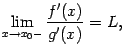
то существует и предел
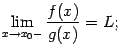
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
аналогичное утверждение верно также для предела справа.
Пример 5.3Найдём предел
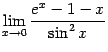 .
.
Этот предел представляет собой предел
отношения двух бесконечно малых,
поскольку
![]() и
и
![]() .
.
Заметим прежде всего, что предел можно
упростить, заменив знаменатель
![]() на
эквивалентную бесконечно малую:
на
эквивалентную бесконечно малую:
![]() при
при
![]() .
Получим:
.
Получим:
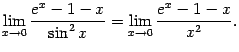
Числитель упростить пока не удаётся, поскольку правила вычисления пределов не позволяют нам заменять на эквивалентные слагаемые (а не множители). В предположении, что предел существует, найдём вместо него предел отношения производных, который, в соответствии с доказанной теоремой, равен исходному:
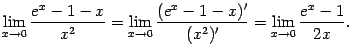
Получившийся предел -- снова предел
отношения бесконечно малых, но его легко
вычислить, заменив числитель на
эквивалентную бесконечно малую:
![]() при
при
![]() .
Получаем:
.
Получаем:
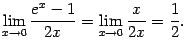
Итак, получили, что предел отношения
производных, действительно, существует
и равен
![]() .
По правилу Лопиталя отсюда следует, что
исходный предел также существует и
равен тому же числу:
.
По правилу Лопиталя отсюда следует, что
исходный предел также существует и
равен тому же числу:
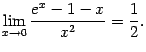
Следовательно,
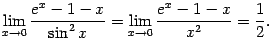
Замечание 5.6Доказанное правило Лопиталя не означает, что если предел отношения производных не существует, то не существует и исходный предел. Этот исходный предел вполне может существовать, только его нельзя найти при помощи применения правила Лопиталя. Иными словами, правило Лопиталяне является универсальнымсредством отыскания пределов отношения двух бесконечно малых. Пример предела, который нельзя отыскать с помощью правила Лопиталя, мы сейчас приведём.
Пример 5.4Рассмотрим предел
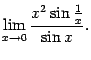 Его
легко вычислить, заметив, что величина
Его
легко вычислить, заметив, что величина
![]() --
величина, локально ограниченная при
базе
--
величина, локально ограниченная при
базе
![]() ,
а величина
,
а величина
![]() --
бесконечно малая:
--
бесконечно малая:
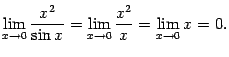
Следовательно, их произведение -- бесконечно малая величина, и
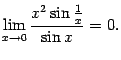
С другой стороны, попробуем применить
к исходному пределу отношения двух
бесконечно малых
![]() и
и
![]() правило
Лопиталя и вычислить предел отношения
производных этих двух функций. Имеем:
правило
Лопиталя и вычислить предел отношения
производных этих двух функций. Имеем:
![]() и
и
![]() .
Составим отношение этих двух производных:
.
Составим отношение этих двух производных:
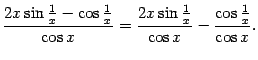
В этом выражении первое слагаемое имеет,
очевидно, при
![]() предел,
равный 0, а второе не имеет никакого
предела; следовательно, не имеет предела
и сумма.
предел,
равный 0, а второе не имеет никакого
предела; следовательно, не имеет предела
и сумма.
Итак, исходное отношение бесконечно малых имеет предел, равный 0, в то время как отношение производных этих бесконечно малых не имеет никакого предела. Получаем, что применение к данному примеру правила Лопиталя не приводит к желаемому вычислению предела.
Правило Лопиталя действует не только
при базах
![]() ,
,
![]() ,
,
![]() ,
но и при базах
,
но и при базах
![]() ,
,
![]() ,
,
![]() .
Докажем это.
.
Докажем это.
Теорема 5.6(Правило Лопиталя для
![]() )Пусть
)Пусть
![]() и
и
![]() --
функции, являющиеся бесконечно малыми
при базе
--
функции, являющиеся бесконечно малыми
при базе
![]() (или
(или
![]() ,
или
,
или
![]() )
и дифференцируемые на некотором луче
)
и дифференцируемые на некотором луче
![]() (или
(или
![]() ,
или объединении лучей
,
или объединении лучей
![]() ,
соответственно). Тогда если существует
предел
,
соответственно). Тогда если существует
предел

то предел
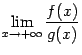 также
существует и равен тому же числу:
также
существует и равен тому же числу:
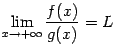
(аналогичные утверждения справедливы
и для баз
![]() ,
,
![]() ).
).
Доказательство.
Положим
![]() и
рассмотрим функции
и
рассмотрим функции
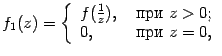 и
и
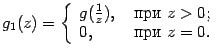 Тогда
функции
Тогда
функции
![]() и
и
![]() непрерывны
на отрезке
непрерывны
на отрезке
![]() и
дифференцируемы при
и
дифференцируемы при
![]() .
При этом
.
При этом
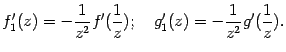
К бесконечно малым при
![]() величинам
величинам
![]() и
и
![]() можно
применить правило Лопиталя ( теорема
5.5 для предела справа, см. замечание
5.5):
можно
применить правило Лопиталя ( теорема
5.5 для предела справа, см. замечание
5.5):
|
|
|
Распространим теперь правило Лопиталя
на случай, когда функции
![]() и
и
![]() являются
бесконечно большими величинами при
данной базе (о бесконечно больших
величинах см. раздел 2.7).
являются
бесконечно большими величинами при
данной базе (о бесконечно больших
величинах см. раздел 2.7).
Теорема 5.7(Правило Лопиталя для отношения бесконечно
больших)Пусть
![]() и
и
![]() при
при
![]() и
в некоторой проколотой окрестности
и
в некоторой проколотой окрестности
![]() ,
,
![]() ,
существуют производные
,
существуют производные
![]() и
и
![]() .
Тогда, если существует предел отношения
этих производных
.
Тогда, если существует предел отношения
этих производных

то существует и предел отношения самих функций, равный тому же числу:
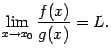
Доказательство. За полным доказательством этого утверждения мы отсылаем к книгам [Никольский С. М.,Курс математического анализа. Том 1. -- М.: Наука, 1990. -- С. 200 - 201] или [Смирнов В. И.,Курс высшей математики. Том 1. -- М.: Наука, 1974. -- С. 157 - 158]. Здесь же мы докажем, что оба предела совпадают, в предположении, что второй из них существует и оба не равны 0. Итак, пусть
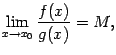
где
![]() --
некоторое число. Докажем, что тогда
--
некоторое число. Докажем, что тогда
![]() .
.
Рассмотрим вспомогательные функции
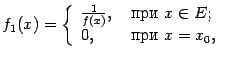 и
и

Тогда функции
![]() и
и
![]() --
бесконечно малые при
--
бесконечно малые при
![]() ,
непрерывные при
,
непрерывные при
![]() ;
их производные таковы:
;
их производные таковы:

Заметим теперь, что при
![]()
|
|
(5.3) |
и
|
|
(5.4) |
Из равенства (5.3) получаем, что
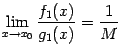 .
Переходя к пределу в равенстве (5.4),
получаем:
.
Переходя к пределу в равенстве (5.4),
получаем:
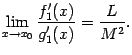
С другой стороны, применяя правило
Лопиталя ( теорема 5.5) к бесконечно малым
функциям
![]() и
и
![]() ,
получим:
,
получим:
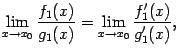
откуда
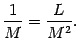
Из этого равенства следует, что
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Замечание
5.7Немного изменив доказательство,
мы получим, что правило Лопиталя для
отношения двух бесконечно больших верно
для односторонних пределов (при базах
![]() и
и
![]() );
сделав замену
);
сделав замену
![]() ,
выведем, что оно верно для пределов при
базах
,
выведем, что оно верно для пределов при
базах
![]() ,
,
![]() и
и
![]() (аналогично
тому, как теорема 5.6 была выведена из
теоремы 5.5).
(аналогично
тому, как теорема 5.6 была выведена из
теоремы 5.5).
Замечание
5.8Как и в основном случае отношения
двух бесконечно малых при
![]() ,
все остальные варианты правила Лопиталя
не универсальны: если предел отношения
производных не существует, то это ещё
не означает, что нет предела отношения
исходных величин.
,
все остальные варианты правила Лопиталя
не универсальны: если предел отношения
производных не существует, то это ещё
не означает, что нет предела отношения
исходных величин.
Приведём ещё один пример, иллюстрирующий это важное замечание.
Пример 5.5Рассмотрим при
![]() две
бесконечно больших:
две
бесконечно больших:
![]() и
и
![]() .
Предел их отношения, очевидно, существует:
.
Предел их отношения, очевидно, существует:
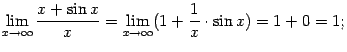
в то же время отношение производных даёт

а эта функция не имеет никакого предела
при
![]() .
Следовательно, для вычисления предела
.
Следовательно, для вычисления предела
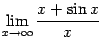
правило Лопиталя неприменимо.
Несмотря на свою неуниверсальность, правило Лопиталя служит весьма мощным средством нахождения сложных пределов. При этом иной раз приходится применять это правило много раз подряд, пока не получим предел, значение которого либо очевидно, либо может быть вычислено каким-либо способом, изученным нами ранее (например, с помощью замены на эквивалентные бесконечно малые).
Пример 5.6Найдём предел
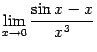 .
(Это предел отношения двух бесконечно
малых. Заметим, что
.
(Это предел отношения двух бесконечно
малых. Заметим, что
![]() не
является множителем, так что его нельзя
заменить на эквивалентную величину
не
является множителем, так что его нельзя
заменить на эквивалентную величину
![]() ;
если бы мы всё же сделали это, то сразу
получили бы в числителе 0, и "ответ"
равнялся бы 0.) Применим правило Лопиталя
и получим, что
;
если бы мы всё же сделали это, то сразу
получили бы в числителе 0, и "ответ"
равнялся бы 0.) Применим правило Лопиталя
и получим, что
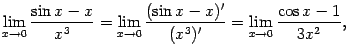
в предположении, что последний предел
существует. Этот последний предел можно
найти, заметив, что
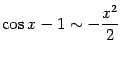 при
при
![]() ,
и заменив числитель. Однако можно пойти
и другим путём. Мы снова получили
отношение двух бесконечно малых, к
которому снова применим правило Лопиталя:
,
и заменив числитель. Однако можно пойти
и другим путём. Мы снова получили
отношение двух бесконечно малых, к
которому снова применим правило Лопиталя:
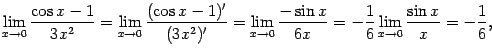
поскольку
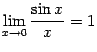 (это
первый замечательный предел).
(это
первый замечательный предел).
Итак, обоснование результата таково:

откуда по теореме 5.5

то есть
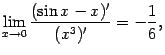
откуда, в свою очередь, снова по теореме 5.5
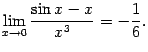
Как правило, при вычислениях эти рассуждения "обратного хода" не приводят в явной форме для экономии места, но, строго говоря, их всегда нужно иметь в виду, когда после цепочки переходов по правилу Лопиталя мы получаем какой-либо ответ к исходному примеру на вычисление предела.
Сравнение бесконечно больших величин
Пусть
![]() --
некоторая база, и
--
некоторая база, и
![]() и
и
![]() --
функции, заданные на некотором окончании
этой базы. В главе 2 мы изучали сравнение
функций
--
функции, заданные на некотором окончании
этой базы. В главе 2 мы изучали сравнение
функций
![]() и
и
![]() при
базе
при
базе
![]() в
случае, когда они является бесконечно
малыми. Здесь же мы изучим сравнение
бесконечно больших
в
случае, когда они является бесконечно
малыми. Здесь же мы изучим сравнение
бесконечно больших
![]() и
и
![]() .
.
Определение
5.1Пусть
![]() --
бесконечно большие величины при базе
--
бесконечно большие величины при базе
![]() .
Ониимеют один и тот же порядок ростапри базе
.
Ониимеют один и тот же порядок ростапри базе
![]() ,
если существует предел
,
если существует предел
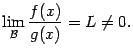
То, что
![]() и
и
![]() имеют
один и тот же порядок роста, обозначим
так:
имеют
один и тот же порядок роста, обозначим
так:
![]()
Если при этом
![]() ,
то бесконечно большие
,
то бесконечно большие
![]() и
и
![]() называютсяэквивалентнымипри базе
называютсяэквивалентнымипри базе
![]() ;
это обозначается так:
;
это обозначается так:
![]()
Если

то величина
![]() имеет
меньший порядок ростапри базе
имеет
меньший порядок ростапри базе
![]() ,
чем величина
,
чем величина
![]() .
Этот факт записывается так:
.
Этот факт записывается так:
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Наконец, если при некотором
![]() имеет
место соотношение
имеет
место соотношение
![]()
то будем говорить, что величина
![]() имеетпорядок роста, равный
имеетпорядок роста, равный
![]() ,
относительно величины
,
относительно величины
![]() .
.
Пример 5.7При
![]() величины
величины
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() --
бесконечно большие. При этом
--
бесконечно большие. При этом
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() имеет
порядок
имеет
порядок
![]() относительно
относительно
![]() ,
,
![]() имеет
порядок 3 относительно
имеет
порядок 3 относительно
![]() и
порядок 6 относительно
и
порядок 6 относительно
![]() ,
,
![]() имеет
порядок 4 относительно
имеет
порядок 4 относительно
![]() и
порядок
и
порядок
![]() относительно
относительно
![]() .
.
В качестве простого упражнения докажите
упомянутые соотношения; легко увидеть
между функциями
![]() ,
,
![]() также
много других соотношений.
также
много других соотношений.
Пример 5.8При
![]() рассмотрим
функции
рассмотрим
функции
![]() (
(![]() )
и
)
и
![]() (
(![]() ).
Покажем, что при всех таких
).
Покажем, что при всех таких
![]() и
и
![]() имеет
место соотношение
имеет
место соотношение
![]()
то есть любая степень
![]() имеет
меньший порядок роста при
имеет
меньший порядок роста при
![]() ,
чем растущая экспонента
,
чем растущая экспонента
![]() .
.
Для этого рассмотрим предел
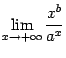 .
К этому пределу можно применить правило
Лопиталя:
.
К этому пределу можно применить правило
Лопиталя:
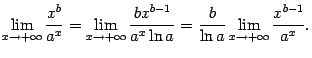
Если при этом
![]() ,
то последний предел берётся от бесконечно
малой и равен 0; если же
,
то последний предел берётся от бесконечно
малой и равен 0; если же
![]() ,
то правило Лопиталя можно применить
ещё раз и, быть может, неоднократно. В
конечном счёте получим
,
то правило Лопиталя можно применить
ещё раз и, быть может, неоднократно. В
конечном счёте получим
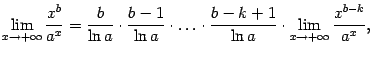
где
![]() (напомним,
что через
(напомним,
что через
![]() обозначается
ближайшее целое число, не меньшее
обозначается
ближайшее целое число, не меньшее
![]() ).
Поскольку
).
Поскольку
![]() ,
в числителе дроби стоит невозрастающая
функция, а знаменатель стремится к
,
в числителе дроби стоит невозрастающая
функция, а знаменатель стремится к
![]() ,
так что предел равен 0, что и требовалось
получить.
,
так что предел равен 0, что и требовалось
получить.
Упражнение
5.1Докажите, что функция
![]() имеет
при
имеет
при
![]() больший
порядок роста, чем
больший
порядок роста, чем
![]() ,
при любом
,
при любом
![]() ,
и, тем более, чем любой многочлен
,
и, тем более, чем любой многочлен
![]()
Пример 5.9При
![]() рассмотрим
функции
рассмотрим
функции
![]() (
(
![]() )
и
)
и
![]() (
(![]() ).
Покажем, что при всех таких
).
Покажем, что при всех таких
![]() и
и
![]() имеет
место соотношение
имеет
место соотношение
![]()
то есть логарифм имеет меньший порядок
роста при
![]() ,
чем любая положительная степень
,
чем любая положительная степень
![]() .
.
Для доказательства вычислим предел
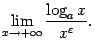 Поскольку
это предел отношения двух бесконечно
больших, можно применить правило
Лопиталя:
Поскольку
это предел отношения двух бесконечно
больших, можно применить правило
Лопиталя:
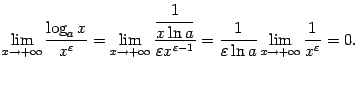
Упражнение
5.2Докажите, что
![]() при
любом, как угодно малом
при
любом, как угодно малом
![]() имеет
больший порядок роста при
имеет
больший порядок роста при
![]() ,
чем любая, сколь угодно большая степень
логарифма
,
чем любая, сколь угодно большая степень
логарифма
![]() ,
(
,
(![]() ,
,
![]() ).
).
Упражнение
5.3Докажите, что при
![]() степенные
функции
степенные
функции
![]() ,
,
![]() ,
имеют тем больший порядок роста, чем
больше значение
,
имеют тем больший порядок роста, чем
больше значение
![]() .
.
Упражнение
5.4Докажите, что
![]() при
любом, как угодно малом
при
любом, как угодно малом
![]() имеет
больший порядок роста при
имеет
больший порядок роста при
![]() ,
чем любая, сколь угодно большая степень
логарифма
,
чем любая, сколь угодно большая степень
логарифма
![]() ,
(
,
(![]() ,
,
![]() ).
).
Упражнение
5.5Выясните, какая из функций имеет
больший порядок роста при
![]() :
а)
:
а)
![]() или
или
![]() ?
б)
?
б)
![]() или
или
![]() ?
?
Пример 5.10Рассмотрим функцию
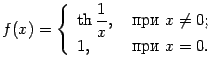 Эта
функция непрерывна справа в точке
Эта
функция непрерывна справа в точке
![]() .
Найдём её производную справа в точке
0, сделав при этом замену
.
Найдём её производную справа в точке
0, сделав при этом замену
![]() :
:
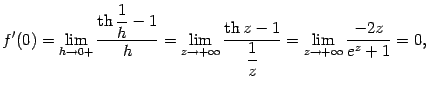
поскольку, как мы выяснили выше, экспонента
![]() растёт
быстрее
растёт
быстрее
![]() при
при
![]() .
.
Во всех остальных точках
![]() производная
вычисляется с помощью правил
дифференцирования:
производная
вычисляется с помощью правил
дифференцирования:
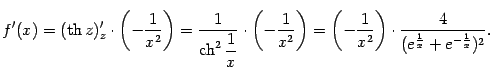
При
![]() это
выражение имеет предел
это
выражение имеет предел
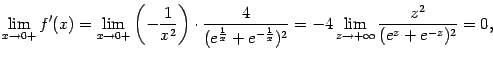
поскольку степень в числителе дроби имеет меньший порядок роста, чем экспонента в знаменателе.
Таким образом, получили, что
![]() ,
то есть производная оказалась непрерывной
справа в точке
,
то есть производная оказалась непрерывной
справа в точке
![]() .
.
Из того, что функция
![]() --
нечётная, нетрудно найти, чему будет
равна производная слева в точке 0 у
функции
--
нечётная, нетрудно найти, чему будет
равна производная слева в точке 0 у
функции
![]() ,
если её переопределить в нуле так, чтобы
она оказалась непрерывной слева. У этой
функции производная слева также будет
существовать во всех точках
,
если её переопределить в нуле так, чтобы
она оказалась непрерывной слева. У этой
функции производная слева также будет
существовать во всех точках
![]() ,
причём эта левая производная будет
всюду непрерывна слева.
,
причём эта левая производная будет
всюду непрерывна слева.
Пример 5.11Рассмотрим функцию
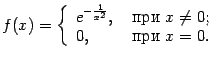
При
![]() её
производная равна, как нетрудно
подсчитать,
её
производная равна, как нетрудно
подсчитать,
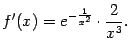
При
![]() мы
найдём производную, исходя из определения:
мы
найдём производную, исходя из определения:
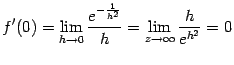
(мы применили формулу
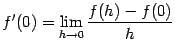 ,
а затем сделали замену
,
а затем сделали замену
![]() ).
Легко видеть, что предел производной
также будет равен 0:
).
Легко видеть, что предел производной
также будет равен 0:
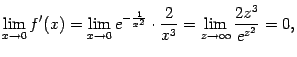
так как
![]() при
при
![]() растёт
быстрее любой степени. Таким образом,
растёт
быстрее любой степени. Таким образом,
![]() --
функция, непрерывная на всей числовой
оси:
--
функция, непрерывная на всей числовой
оси:
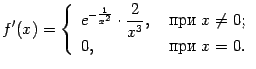
Аналогично можно убедиться, что

непрерывная на
![]() функция,
и вообще, при любом номере
функция,
и вообще, при любом номере
![]() производная
производная
![]() имеет
вид
имеет
вид

где
![]() --
некоторый многочлен переменного
--
некоторый многочлен переменного
![]() .
Легко видеть, что эта функция непрерывна
при
.
Легко видеть, что эта функция непрерывна
при
![]() .
.
Таким образом, мы получили важный пример
функции, которая всюду имеет производные
любого порядка, и при этом в точке 0 все
эти производные равны 0, в то время как
сама функция отлична от 0 при всех
![]() .
.
Упражнение 5.6Рассмотрите функцию
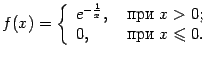
Покажите, что все её производные
существуют при всех
![]() и
непрерывны; при этом
и
непрерывны; при этом
![]() для
любого
для
любого
![]() .
.
Алгебраические структуры
Современная алгебра как раздел математики занимается вопросами, связанными с множествами, на которых заданы некоторые операции. Причем с точки зрения алгебры совершенно безразлично, из каких элементов состоит множество, важно лишь, какими свойствами обладают имеющиеся на этом множестве операции. Чаще всего под операцией подразумевается правило (закон), по которому двум элементам из множества, взятым в определенном порядке, сопоставляется третий элемент из этого множества. Такие операции называются бинарными.
Если, например, взять множество
действительных чисел, то операциями
являются сложение и умножение чисел.
Если взять множество квадратных матриц,
то для них тоже определены операции
сложения и умножения. Но в этом случае,
в отличие от множества чисел, умножение
обладает другими свойствами, например,
оно некоммутативно, и не всегда можно
решить уравнение
![]() .
.
Как правило, в алгебре бинарная операция
называется или сложением, или умножением
и для нее используются обычные обозначения
"+" или "![]() ", но это не означает, что операция
непременно обладает теми же свойствами
сложения или умножения, к которым мы
привыкли в школе. В начале, чтобы избежать
недоразумений, будем обозначать операцию
каким-нибудь экзотическим символом,
например "
", но это не означает, что операция
непременно обладает теми же свойствами
сложения или умножения, к которым мы
привыкли в школе. В начале, чтобы избежать
недоразумений, будем обозначать операцию
каким-нибудь экзотическим символом,
например "![]() ", то есть
", то есть
![]() --
результат применения операции к элементам
--
результат применения операции к элементам
![]() и
и
![]() ,
причем
,
причем
![]() --
первый элемент (первый операнд),
--
первый элемент (первый операнд),
![]() --
второй (второй операнд).
--
второй (второй операнд).
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример 16.1Пусть множество
![]() состоит
только из двух элементов. Один обозначим
состоит
только из двух элементов. Один обозначим
![]() ,
а другой обозначим
,
а другой обозначим
![]() ,
то есть
,
то есть
![]() .
Тогда можно образовать с учетом порядка
элементов только четыре пары:
.
Тогда можно образовать с учетом порядка
элементов только четыре пары:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Пусть
.
Пусть
![]()
Это пример множества, на котором введена одна операция. На первый взгляд данный пример может показаться очень искусственным, лишенным всякого смысла. Однако это не так, он используется в математической логике, это операция исключающего илиилисложение по модулю два.
Если на произвольном множестве задать произвольно некторую операцию, то как правило, ничего интересного из этого образования извлечь не удастся. Поэтому на операции накладываются дополнительные ограничения, и в зависимости от этих ограничений получаются разные алгебраические структуры, то есть разные типы множеств с операциями. Далее мы рассмотрим несколько алгебраических структур, а именно, группы, кольца, поля, линейные пространства.

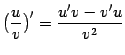
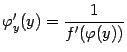
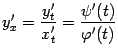 (см. ниже)
(см. ниже)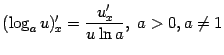 ,
,