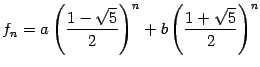- •Функции и их графики Конспекты, лекции, задачи
- •Первый способ задания функции: табличный
- •Clx.Ru - реклама в интернет
- •Упражнения
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
- •Сводка основных результатов о производных
- •Формула Тейлора теория и практика в примерах Многочлен Тейлора
- •Исследование функций и построение графиков Асимптоты графика функции
- •Достаточные условия локального экстремума
- •Примеры исследования функций и построения графиков
Первый способ задания функции: табличный
Если множество
![]() конечно
и состоит из
конечно
и состоит из![]() элементов
элементов![]() ,
то функцию можно задать перечислением,
указав, какие значения она принимает
на каждом элементе
,
то функцию можно задать перечислением,
указав, какие значения она принимает
на каждом элементе![]() .
Часто это делают в виде таблицы:
.
Часто это делают в виде таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
В верхней строке таблицы перечисляются
все
![]() элементов
конечного множества
элементов
конечного множества![]() ,
а в нижней -- соответствующие им
значения функции. Разумеется, таблицу
можно расположить и в два столбца вместо
двух строк.
,
а в нижней -- соответствующие им
значения функции. Разумеется, таблицу
можно расположить и в два столбца вместо
двух строк.
Пример 1.10В отделе кадров составляют таблицу,
в которой в первом столбце содержатся
фамилии и инициалы работников, а во
втором -- серии и номера их паспортов.
Такая таблица задаёт функцию![]() --
соответствие между множеством
--
соответствие между множеством![]() работников
предприятия и множеством
работников
предприятия и множеством![]() кодов
(код -- это серия и номер) паспортов.
Полученная таблица может выглядеть,
например, так:
кодов
(код -- это серия и номер) паспортов.
Полученная таблица может выглядеть,
например, так:
|
Фамилия И.О. |
Паспорт: серия, |
номер |
|
Абрамов В.П. |
II-СИ |
356531 |
|
Бархударов Ш.Х. |
VII-ПЮ |
785305 |
|
Виноградов А.В. |
XII-ЧФ |
015628 |
|
Гусева Т.И. |
IV-БШ |
764285 |
|
... |
... |
|
![]()
![]() CLX.ru
- реклама в интернет Определённая
таким способом функция
CLX.ru
- реклама в интернет Определённая
таким способом функция![]() --
это инъекция, так как ни у каких двух
человек не могут оказаться паспорта с
одинаковым кодом (серия, номер).
--
это инъекция, так как ни у каких двух
человек не могут оказаться паспорта с
одинаковым кодом (серия, номер).
Другая форма таблицы удобна для функции
![]() ,
заданной на прямом произведении двух
множеств
,
заданной на прямом произведении двух
множеств![]() и
и![]() ,
то есть когда
,
то есть когда![]() ,
причём множества
,
причём множества![]() и
и![]() конечные:
конечные:![]() и
и![]() .
Перечислим все элементы множества
.
Перечислим все элементы множества![]() по
вертикали, а
по
вертикали, а![]() --
по горизонтали. В пересечениях строки
и столбца, содержащих элементы
--
по горизонтали. В пересечениях строки
и столбца, содержащих элементы![]() и
и![]() ,
укажем значение функции
,
укажем значение функции![]() ,
где
,
где![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как мы видим, задание такой функции
эквивалентно заданию прямоугольной
таблицы -- матрицы размера
![]() ,
элементами которой являются элементы
множества
,
элементами которой являются элементы
множества![]() .
.
Пример 1.11В теории игр (одной из областей
математики) рассматривается, в частности,
такая задача. При взаимодействии двух
партнёров![]() и
и![]() каждый
из них может получить выигрыш, зависящий
от вариантов действий каждого партнёра.
Пусть множества вариантов действий
(эти варианты называютсястратегиями)
партнёров конечны:
каждый
из них может получить выигрыш, зависящий
от вариантов действий каждого партнёра.
Пусть множества вариантов действий
(эти варианты называютсястратегиями)
партнёров конечны:![]() может
выбирать одну из стратегий из множества
может
выбирать одну из стратегий из множества![]() ,
а
,
а![]() --
из множества
--
из множества![]() .
Если
.
Если![]() выбрал
стратегию
выбрал
стратегию![]() ,
а
,
а![]() --
стратегию
--
стратегию![]() ,
то однозначно определены выигрыши: у
первого партнёра он равен числу
,
то однозначно определены выигрыши: у
первого партнёра он равен числу![]() ,
а у второго -- числу
,
а у второго -- числу![]() .
Рассмотрим функцию
.
Рассмотрим функцию![]() ,
такую что
,
такую что
![]()
Эта функция называется функцией выигрышейилиплатёжным отображениемигры. Её можно полностью задать, сведя все данные в таблицу вида
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть задав одну матрицу, элементы
которой -- пары чисел
![]() ,
или же задав две числовые матрицы
,
или же задав две числовые матрицы![]() и
и![]() размера
размера![]() :
:
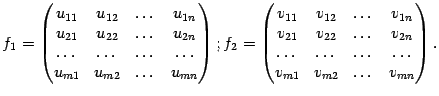
Второй способ задания функции: с помощью формулы
Если множество
![]() бесконечно,
то способ перечисления значений уже не
годится. В этом случае функция
бесконечно,
то способ перечисления значений уже не
годится. В этом случае функция
![]() может
быть задана некоторой формулой,
позволяющей по каждому значению аргумента
может
быть задана некоторой формулой,
позволяющей по каждому значению аргумента
![]() найти
соответствующее ему значение
найти
соответствующее ему значение
![]() ,
например:
,
например:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание
1.3Функции, заданныеодной и той
жеформулой, но наразныхмножествах
![]() ,
считаютсяразличными. Так, функция
,
считаютсяразличными. Так, функция
![]() при
при
![]() и
функция
и
функция
![]() при
при
![]() --
это дверазныефункции, так как
функция
--
это дверазныефункции, так как
функция
![]() устанавливает
соответствие между точками множества
устанавливает
соответствие между точками множества
![]() и
некоторыми точками числовой прямой, а
функция
и
некоторыми точками числовой прямой, а
функция
![]() --
между точкамидругогомножества
--
между точкамидругогомножества
![]() и
точками числовой прямой. Конечно, две
эти функции -- "близкие родственники",
так как
и
точками числовой прямой. Конечно, две
эти функции -- "близкие родственники",
так как
![]() при
всех
при
всех
![]() .
.
Определение
1.6Если дана функция
![]() ,
и
,
и
![]() ,
то мы можем получить новую функцию,
рассматривая значения функции
,
то мы можем получить новую функцию,
рассматривая значения функции
![]() только
на элементах
только
на элементах
![]() .
Эта функция
.
Эта функция
![]() определена
равенством
определена
равенством
![]() при
при
![]() .
Функция
.
Функция
![]() называетсяограничениемфункции
называетсяограничениемфункции
![]() на
подмножество
на
подмножество
![]() её
области определения
её
области определения
![]() и
обозначается
и
обозначается
![]() ,
то есть
,
то есть
![]() .
.
Пример 1.12Пусть
![]() --
числовая плоскость и функция
--
числовая плоскость и функция![]() задана формулой
задана формулой
![]()
Рассмотрим на плоскости
![]() подмножество --
прямую линию
подмножество --
прямую линию
![]() ,
заданную уравнением
,
заданную уравнением
![]() .
Тогда мы можем рассмотреть в качестве
аргументов функции
.
Тогда мы можем рассмотреть в качестве
аргументов функции
![]() точки
только прямой
точки
только прямой
![]() .
Ограничение
.
Ограничение
![]() определено
только при
определено
только при
![]() ,
поэтому его, кроме исходной формулы
,
поэтому его, кроме исходной формулы
![]()
можно задать такими формулами:
|
|
(1.1) |
(так как
![]() на
прямой
на
прямой
![]() ),
или
),
или
|
|
(1.2) |
(так как
![]() на
прямой
на
прямой
![]() ).
Во всех точках
).
Во всех точках
![]() прямой
прямой
![]() все
три формулы дают одно и то же значение
функции
все
три формулы дают одно и то же значение
функции
![]() .
Мы видим, что формула (1.1) даёт для
.
Мы видим, что формула (1.1) даёт для
![]() те
же значения, что функцияодногопеременного
те
же значения, что функцияодногопеременного
![]() :
:
![]() ,
а формула (1.2) -- те же значения, что
функция одного переменного
,
а формула (1.2) -- те же значения, что
функция одного переменного
![]() :
:
![]() .
.
Две последние функции называются
параметризациямиограничения
![]() .
.
Пример 1.13Пусть
![]() --
функция, заданная во всех точках плоскости
--
функция, заданная во всех точках плоскости
![]() .
Пусть
.
Пусть
![]() --
прямая
--
прямая
![]() на
плоскости
на
плоскости
![]() .
Тогда функция
.
Тогда функция
![]() равна
равна
![]() .
Формально ограничение зависит от точек
.
Формально ограничение зависит от точек
![]() плоскости
плоскости
![]() ,
но только таких, что
,
но только таких, что
![]() .
Поэтому задание этого ограничения
.
Поэтому задание этого ограничения
![]() эквивалентно
заданию числовой функцииодного
переменного
эквивалентно
заданию числовой функцииодного
переменного
![]() .
Функция
.
Функция
![]() --
это одна из возможных параметризаций
функции
--
это одна из возможных параметризаций
функции
![]() .
.
Замечание
1.4Во многих учебных примерах при
задании функции
![]() при
помощи формулы не указывают область
определения
при
помощи формулы не указывают область
определения
![]() .
При этом по умолчанию предполагается,
что область определения
.
При этом по умолчанию предполагается,
что область определения
![]() --
максимально допустимая, то есть она
состоит из всех таких значений аргумента
--
максимально допустимая, то есть она
состоит из всех таких значений аргумента
![]() ,
для которых задающее функцию
,
для которых задающее функцию
![]() выражение
выражение
![]() имеет
смысл. При этом могут возникнуть трудности
с выяснением того, какова же именно
область
имеет
смысл. При этом могут возникнуть трудности
с выяснением того, какова же именно
область
![]() ,
если в этом возникнет необходимость.
,
если в этом возникнет необходимость.
Пример 1.14Пусть функция
![]() задана
формулой
задана
формулой
![]()
По умолчанию считается, что области
![]() принадлежат
все те точки
принадлежат
все те точки
![]() ,
что
,
что
![]() .
Разумеется, для каждой заданной точки
.
Разумеется, для каждой заданной точки
![]() проверить
это условие несложно, однако описать
множество
проверить
это условие несложно, однако описать
множество
![]() в
виде объединения промежутков числовой
оси мы не сможем ввиду того, что
затрудняемся решить "в явном виде"
данное неравенство.
в
виде объединения промежутков числовой
оси мы не сможем ввиду того, что
затрудняемся решить "в явном виде"
данное неравенство.
Если
![]() --
это множество натуральных чисел
--
это множество натуральных чисел
![]() ,
то функция
,
то функция
![]() называетсяпоследовательностью. Так как
называетсяпоследовательностью. Так как
![]() содержит
бесконечное множество чисел
содержит
бесконечное множество чисел
![]() ,
то задать
,
то задать
![]() в
виде таблицы значений
в
виде таблицы значений
![]() ,
где
,
где
![]() ,
вообще говоря, нельзя. Однако если
функция
,
вообще говоря, нельзя. Однако если
функция
![]() легко
угадывается по своим значениям
легко
угадывается по своим значениям
![]() при
небольших
при
небольших
![]() ,
её часто задают, выписывая таблицу
нескольких первых значений.
,
её часто задают, выписывая таблицу
нескольких первых значений.
Пример 1.15Пусть
![]() .
Тогда, скорее всего, имеется в виду, что
.
Тогда, скорее всего, имеется в виду, что
![]() при
любом
при
любом
![]() .
Эта формула не противоречит выписанным
значениям
.
Эта формула не противоречит выписанным
значениям
![]() и
очень проста. По-видимому, именно её и
имели в виду при выписывании первых
членов последовательности. Однако можно
подобрать и другие формулы, то есть
указать другие функции, для которых
получаются те же первые значения
и
очень проста. По-видимому, именно её и
имели в виду при выписывании первых
членов последовательности. Однако можно
подобрать и другие формулы, то есть
указать другие функции, для которых
получаются те же первые значения
![]() ,
но, быть может, другие значения
,
но, быть может, другие значения
![]() .
.
Упражнение
1.1Придумайте другую формулу,
дающую те же самые значения
![]() ,
но при всех прочих
,
но при всех прочих
![]() (
(
![]() )
дающую значения, не равные
)
дающую значения, не равные
![]() .
.
Указание: попробуйте, например,
отыскать эту формулу в виде
![]() ,
подобрав коэффициенты
,
подобрав коэффициенты
![]() так,
чтобы формула была верна при
так,
чтобы формула была верна при
![]() .
Получится система трёх линейных уравнений
для трёх неизвестных
.
Получится система трёх линейных уравнений
для трёх неизвестных
![]() ,
рещив которую, вы найдёте, что
,
рещив которую, вы найдёте, что
![]() .
.
В некоторых случаях члены последовательности,
то есть значения
![]() для
для
![]() ,
удобно не задавать при помощи указания
явной зависимости
,
удобно не задавать при помощи указания
явной зависимости
![]() ,
а вычислятьрекуррентно, то есть
вычислять каждый последующий член по
значениям нескольких предыдущих:
,
а вычислятьрекуррентно, то есть
вычислять каждый последующий член по
значениям нескольких предыдущих:
![]()
Пример 1.16Последовательностьчисел Фибоначчи
![]() задаётся
так: два первых члена полагают равными
единице (
задаётся
так: два первых члена полагают равными
единице (
![]() ),
а при
),
а при
![]() вычисляют
вычисляют
![]() по
формуле
по
формуле
![]() .
Таким образом,
.
Таким образом,
![]() и т. д.
и т. д.
Упражнение
1.2Подберите коэффициенты
![]() и
и
![]() в
формуле
в
формуле
|
|
(1.3) |
так, чтобы при
![]() и
и
![]() число
число
![]() было
числом Фибоначчи. Докажите, что тогда
формула (1.3)
даёт значение
было
числом Фибоначчи. Докажите, что тогда
формула (1.3)
даёт значение
![]() ,
равное числу Фибоначчи и при всех
,
равное числу Фибоначчи и при всех
![]() .
.
Пусть
 (это
один из корней уравнения
(это
один из корней уравнения
![]() ,
служащегохарактеристическим уравнениемвозвратной последовательности
,
служащегохарактеристическим уравнениемвозвратной последовательности
![]() ).
Покажите, что
).
Покажите, что
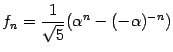
при всех
![]() (формула
Бине); выведите из этой формулы, что
(формула
Бине); выведите из этой формулы, что
![]() --
это ближайшее к
--
это ближайшее к
![]() целое
число.
целое
число.
Обзор некоторых элементарных функций
Для напоминания и повторения приведём обзор некоторых функций, изучаемых в школьной программе.
1. Линейная функция.Это функция вида
![]() .
Число
.
Число
![]() называетсяугловым коэффициентом, а число
называетсяугловым коэффициентом, а число
![]() --свободным членом. Графиком
--свободным членом. Графиком
![]() линейной
функции служит прямая на координатной
плоскости
линейной
функции служит прямая на координатной
плоскости
![]() ,
не параллельная оси
,
не параллельная оси
![]() .
.
Угловой коэффициент
![]() равен
тангенсу угла
равен
тангенсу угла
![]() наклона
графика
наклона
графика
![]() к
горизонтальному направлению --
положительному направлению оси
к
горизонтальному направлению --
положительному направлению оси
![]() .
.

Рис.1.8.График линейной функции -- прямая
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
2. Квадратичная функция.Это функция
вида
![]() (
(![]() ).
).
Графиком
![]() квадратичной
функции служитпараболас осью,
параллельной оси
квадратичной
функции служитпараболас осью,
параллельной оси
![]() .
При
.
При
![]() вершина
параболы оказывается в точке
вершина
параболы оказывается в точке
![]() .
.
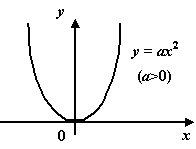
Рис.1.9.Парабола
![]() (
(![]() )
)
В общем случае вершина лежит в точке
![]() .
Если
.
Если
![]() ,
то "рога" параболы направлены
вверх, если
,
то "рога" параболы направлены
вверх, если
![]() ,
то вниз.
,
то вниз.
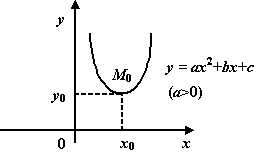
Рис.1.10.Парабола
с вершиной в точке
![]() (
(![]() )
)
3. Степенная функция.Это функция
вида
![]() ,
,
![]() .
Рассматриваются такие случаи:
.
Рассматриваются такие случаи:
а). Если
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ;
если число
;
если число
![]() --
чётное, то и функция
--
чётное, то и функция
![]() --
чётная (то есть
--
чётная (то есть
![]() при
всех
при
всех
![]() );
если число
);
если число
![]() --
нечётное, то и функция
--
нечётное, то и функция
![]() --
нечётная (то есть
--
нечётная (то есть
![]() при
всех
при
всех
![]() ).
).

Рис.1.11.График
степенной функции при
![]()
б). Если
![]() ,
,
![]() ,
то
,
то
![]() .
Ситуация с чётностью и нечётностью при
этом такая же, как и для
.
Ситуация с чётностью и нечётностью при
этом такая же, как и для
![]() :
если
:
если
![]() --
чётное число, то и
--
чётное число, то и
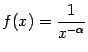 --
чётная функция; если
--
чётная функция; если
![]() --
нечётное число, то и
--
нечётное число, то и
![]() --
нечётная функция.
--
нечётная функция.
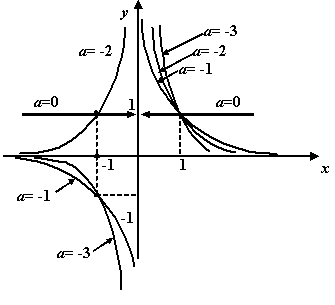
Рис.1.12.График
степенной функции при
![]()
Снова заметим, что
![]() при
всех
при
всех
![]() .
Если
.
Если
![]() ,
то
,
то
![]() при
всех
при
всех
![]() ,
кроме
,
кроме
![]() (выражение
(выражение
![]() не
имеет смысла).
не
имеет смысла).
в). Если
![]() --
не целое число, то, по определению, при
--
не целое число, то, по определению, при
![]() :
:
![]() ;
тогда
;
тогда
![]() ,
,
![]() .
.
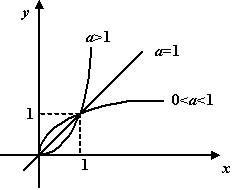
Рис.1.13.График
степенной функции при
![]()
При
![]() ,
по определению,
,
по определению,
![]() ;
тогда
;
тогда
![]() .
.
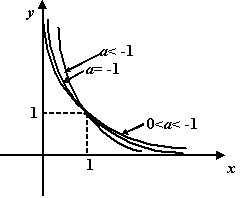
Рис.1.14.График
степенной функции при
![]()
4. Многочлен.Это функция вида
![]() ,
где
,
где
![]() ,
,
![]() .
Число
.
Число
![]() называетсястепеньюмногочлена. При
называетсястепеньюмногочлена. При
![]() и
и
![]() многочлены
являются соответственно линейной
функцией и квадратичной функцией
(квадратным трёхчленом) и рассмотрены
выше. При
многочлены
являются соответственно линейной
функцией и квадратичной функцией
(квадратным трёхчленом) и рассмотрены
выше. При
![]() и
и
![]() (
(
![]() )
получается степенная функция, которую
мы также рассмотрели выше. В общем случае
)
получается степенная функция, которую
мы также рассмотрели выше. В общем случае
![]() ;
при чётном значении степени
;
при чётном значении степени
![]() характерный
вид графика таков:
характерный
вид графика таков:
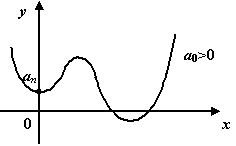
Рис.1.15.График
многочлена чётной степени при
![]()