Упражнения

Упражнение 1.6Пусть,,,. Тогда определены композициии. Докажите, что приимеет место равенство. Выясните также, чему равна функцияи каков её график.

Упражнение 1.7Вспомните материал школьного курса математики и постройте графики следующих функций. Найдите области определения и области значений этих функций.

а) ;

CLX.ru - реклама в интернет

б) ;

в) ;

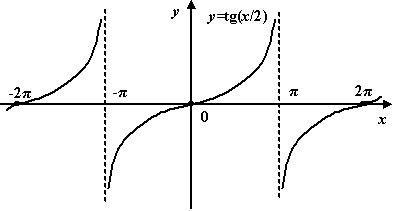
г) ;

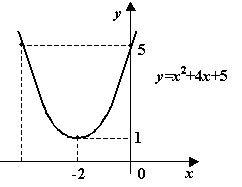
д) ;

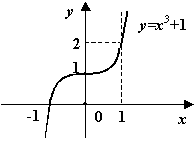
е) ;

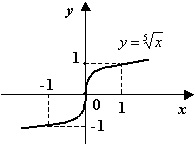
ж) ;

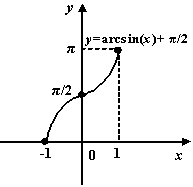
CLX.ru - реклама в интернет

з) ;

и) ;

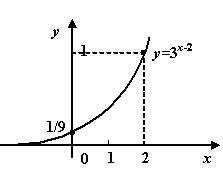
к) ;

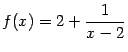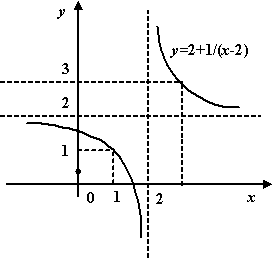
л) ;

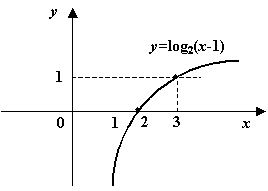
м) ;

н) .

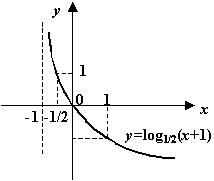
Ответы:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к) ;

л) ;

м) ;

н) .

Упражнение 1.8Найдите области определения и области значений следующих функций:

а) ;

б) ;

в) ;

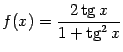г) ;

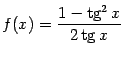д) ;

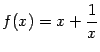е) ;

ж) ;

з) ;

и) ;

к) ;

л) ;

м) .

Какие из этих функций из области в областьявляются биекциями?

Ответы:

Биекциями являются функции пп. е), з), и), л), пpичём все эти четыpе функции-- тождественные отобpажения:

пpи соответствующих областях . Все остальные функции-- не биекции.

а) ;

б) ;

в) (заметим, чтопpи.

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к) ;

л) ;

м) .

Упражнение 1.9Постройте графики функций:

а)

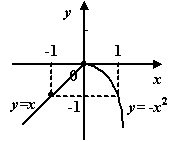
б)

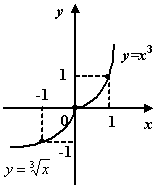
в) ;

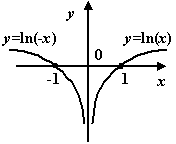
г)

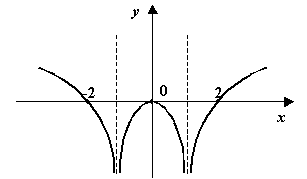
д)

е) ;

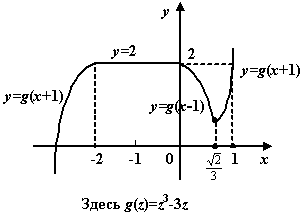
ж) ;

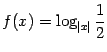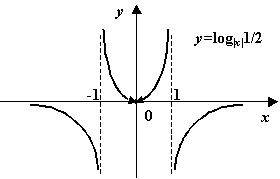
з) ; p class=pic>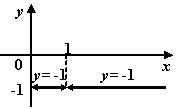

и) .

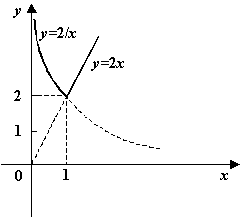
Найдите области опpеделения и области значений этих функций. Какие из этих функций являются биекциями? Если-- биекция, найдите обратную функциюи постройте её график.

Ответы:

Биекцией является только функция п.б), пpи этом

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) .

Упражнение 1.10Последовательностьзадана формулой. Найдите такие числаи, что для любого,, выполняется рекуррентная формула.

Упражнение 1.11Последовательностьзадана рекуррентной формулойпри, причем,. Найдите такие числаи, что при всехвыполняется формула.

Упражнение 1.12Пусть первые члены последовательноститаковы:,,. Найти такие формулы, чторавняется заданным числам при n=1,2,3, причем при некоторыхформула имеет вид:

а) ;

б) ;

в) ;

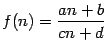г) .

Упражнение 1.13Приведите примеры и постройте графики функций, обладающих следующими свойствами:

а) , причем-- биекция;

б) , причеми каждое своё значениефункция принимает ровно по два раза, то есть для любогосуществуют ровно две точкии(), такие что;

в) , причем-- биекция;

г) , причем-- сюръекция и каждое целое значениепринимается ровно по одному разу, а каждое нецелое значение-- ровно по два раза.

д) , причем-- сюръекция и каждое целое значениепринимается ровно по два раза, а каждое нецелое значение-- ровно по одному разу.

е) , причемпринимает все вещественные значения, кроме целых чётных, и каждое целое нечётное значение принимается ровно по два раза, а каждое нецелое значение-- ровно по одному разу.

Пределы при разных условиях. Некоторые частные случаи

Пусть задана некоторая меняющаяся величина , зависящая от переменного . Предположим, что это переменное можно менять так, что выполняется некотороеусловие : переменное "приближается" ("стремится") к чему-нибудь (что это означает, мы уточним позже при помощи строгих определений). Тогда встаёт вопрос о том, не ведёт ли себя величина каким-либо "правильным" образом, тоже "стремясь" к чему-нибудь, например, к числу . Если это так, то это "что-то" называетсяпределомвеличины при данном условии для и обозначается

Дадим теперь строгие определения предела в некоторых частных случаях, а потом перейдём к обсуждению общего определения.

Определение 2.1Предел функции при .

CLX.ru - реклама в интернет

Пусть -- это функция вещественного переменного , определённая во всех точках интервала , кроме, быть может, точки . Дадим определение предела величины при условии, что стремится к точке . Это условие кратко обозначается . Стремление к означает, что при своём изменении оказывается во всё более узких окрестностях, окружающих точку , но не совпадает с , то есть значение становится всё меньше и меньше, приближаясь к 0, но нулём не становится. При этом может оказаться, что соответствующие значения становятся всё ближе и ближе к некоторому фиксированному числу , причём для любой, сколь угодно малой, окрестности числа можно указать, насколько близко должен подойти к , чтобы значения уже попадали в эту окрестность числа . Тогда число есть предел функции при условии , что записывается так:

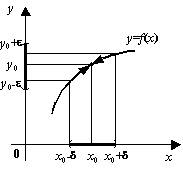
Рис.2.1.Предел при

Формализуем сказанное для придания большей математической ясности. Любая окрестность точки (симметричная относительно ) характеризуется её полушириной , то есть имеет вид интервала . Если значение попало в такую -окрестность, то это означает, что . Любая окрестность точки , не содержащая самой точки (и симметричная относительно ),-- это объединение двух смежных интервалов . Попадание точки в эту окрестность означает, что выполнено неравенство и . Равенство означает тогда, что

для любого, сколь угодно малого, числа можно найти такое число (зависящее от ),что при будет .

CLX.ru - реклама в интернет

При этом число называетсяпределом функции при условии . Тот факт, что , записывают ещё в виде

Пример 2.1Пусть и рассматривается функция . Покажем, что

Для этого фиксируем произвольное число , задающее окрестность , и выясним, при каких значения функции будут попадать в эту окрестность точки1.

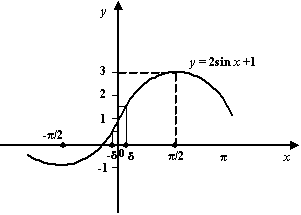
Рис.2.2.График

Попадание значений в окрестность означает, что выполняется неравенство , то есть . При этом нас интересуют только те решения этого неравенства, которые лежат вблизи точки . Решая неравенство, получаем, что оно выполняется при . Таким образом, если взять (это число больше 0), то при будет выполнено неравенство , что и означает, что предел равен числу 1: , или .

Рассмотрим теперь другой важный случай предела.

Определение 2.2Предел последовательности при .

Пусть дана бесконечная последовательность чисел, занумерованных по порядку:

(Эту последовательность можно рассматривать как функцию , определённую при всех натуральных значениях аргумента .) Дадим определение предела последовательности при условии, что номер неограниченно растёт (это условие обозначается ). Стремление к бесконечности означает, что при своём изменении номер становится большим любого наперёд заданного числа , то есть начинает выполняться неравенство . Если при этом числа становятся всё ближе к некоторому фиксированному числу , то это число-- предел последовательности, что записывается так:

Рис.2.3.Последовательность и её предел

Формализуем сказанное. Множества чисел , заданные условиями , можно назвать окрестностями бесконечности. Равенство означает тогда, что

для любого, сколь угодно малого, числа можно найти такое число (зависящее от ),что при (то есть в достаточно далёкой окрестности бесконечностибудет выполняться неравенство .

При этом число называетсяпределом последовательности при условии . Тот факт, что , записывают также в виде

Пример 2.2Покажем, что предел последовательности 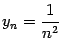равен 0.

Рис.2.4.Последовательность

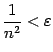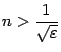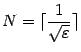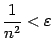Фиксируем произвольное число и подберём число в зависимости от так, чтобы при выполнялось неравенство , то есть . Решая это неравенство, получаем, что оно выполняется при . Значит, достаточно выбрать в качестве натуральное число, ближайшее к справа на вещественной оси, то есть , и тогда при любом неравенство будет верным. Это означает, что

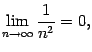
или .

Совершенно аналогично определению предела последовательности выглядит следующее определение.

Определение 2.3Предел функции при условии .

Определим окрестности бесконечности как множества точек , заданные неравенствами , то есть лучи . Потребуем, чтобы для любой, сколь угодно малой, окрестности точки можно было найти такую окрестность бесконечности , что при попадании в эту окрестность, то есть при , соответствующее значение попадает в заданную вначале окрестность точки , то есть выполняется неравенство . Выполнение этого требования будет означать, что -- предел функции при условии , то есть

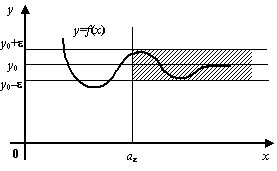
Рис.2.5.Предел при

Тот факт, что , записывают ещё в виде

Пример 2.3Покажем, что предел функци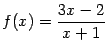и при равен числу 3.

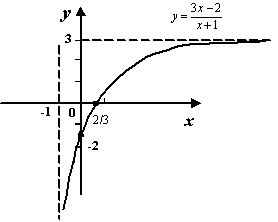
Рис.2.6.График функции

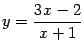
Фиксируем и подберём по этому числу такое число , что при любом выполняется неравенство

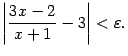
Сразу будем считать, что -- неотрицательное число. Неравенство можно записать в виде 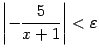или 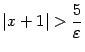. Так как , то и неравенство имеет вид 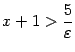, откуда 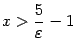. Если теперь взять число равным (или равным 0, если эта разность отрицательна), то при будет выполняться неравенство 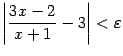; это означает, что

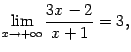
или .

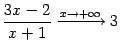Упражнение 2.1Опираясь на свою интуицию и здравый смысл, сформулируйте определение предела функции при условии . Для этого ответьте на предварительный вопрос: какие множества естественно назвать окрестностями ?

Рис.2.7.Предел при

Пользуясь этим определением, покажите, что .

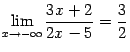Общее определение предела

Заметим, что во всех определениях предыдущего пункта ключевым оказывалось определение набора тех множеств, в которые последовательно, при своём изменении в соответствии с рассматриваемым условием, попадает переменное (или ), от которого зависит изменяющаяся величина (или ). В случае условия эти множества имеют вид ; в случае -- вид ; в случае -- вид . Назовём ихокончаниями базыпредела при данном условии, а полный набор таких окончаний--базой предела. Базу предела будем обозначать так же, как само условие, а именно, , , и т.п. Таким образом,