Исследование функций и построение графиков Асимптоты графика функции

Назовём асимптотамипрямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1Вертикальной асимптотойграфика функцииназывается вертикальная прямая, еслиилипри каком-либо из условий:,,. Заметим, что мы при этом не требуем, чтобы точкапринадлежала области определения функции, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:или, где.

        Пример 7.1Рассмотрим функцию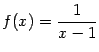. Графикимеет вертикальную асимптоту, поскольку привыполняется условие, а также привыполняется условие.

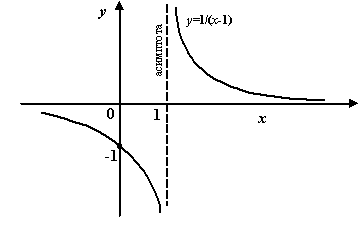
Рис.7.1.Вертикальная асимптота функции CLX.ru - реклама в интернет

        Пример 7.2Рассмотрим функцию. Её график имеет вертикальную асимптоту, так какпри. То, что прифункцияне стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямаяявлялась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать,при.)

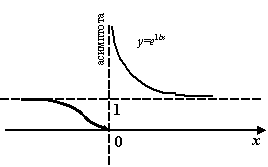
Рис.7.2.Вертикальная асимптота функции

        Пример 7.3Рассмотрим функцию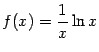. Прямаяявляется вертикальной асимптотой графика, так какпри. Заметим, что слева от точкифункция вообще не определена.

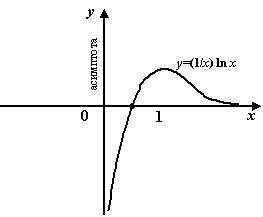
Рис.7.3.Вертикальная асимптота функции

        Пример 7.4График функци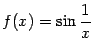ине имеет привертикальной асимптоты, так как-- ограниченная (числом 1) и, следовательно, локально ограниченная прии не стремящаяся к бесконечности функция. Хотя аргумент синуса -- функция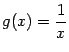-- имеет вертикальную асимптоту.

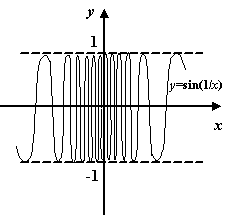
Рис.7.4.График функции 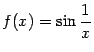не имеет вертикальной асимптоты

        Пример 7.5Прямаяне является вертикальной асимптотой графика функции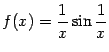, поскольку здесь нельзя утверждать, что приилифункция стремится к бесконечности. При некоторых малых значенияхзначениямогут быть как угодно велики, однако при других малыхфункция обращается в 0: так, при() значения функции равныи стремятся к бесконечности при, а при всехвида() значения функции равны 0. В то же время как те, так и другие точкипри увеличениипопадают всё ближе и ближе к точке 0. Значит, функцияне является бесконечно большой при, и прямая-- не асимптота.

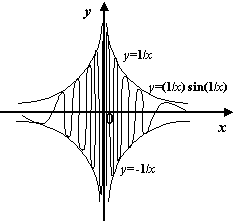
Рис.7.5.График функции не имеет вертикальной асимптоты

Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности.

        Определение 7.2Наклонной асимптотойграфика функцииприназывается прямая, если выполнены два условия: 1) некоторый лучцеликом содержится в; 2) расстояние по вертикали между графиком и прямой стремится к 0 при:

(7.1)

Наклонной асимптотойграфика функцииприназывается прямая, если 1) некоторый лучцеликом содержится в; 2) расстояние по вертикали между графиком и прямой стремится к 0 при:

    

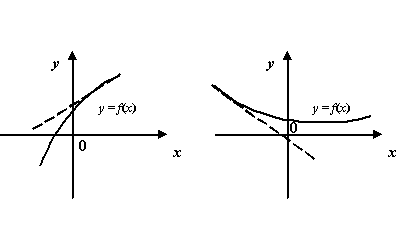
Рис.7.6.Графики функций, имеющие наклонные асимптоты при и при

В случае, если наклонная асимптота расположена горизонтально, то есть при , она называетсягоризонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямаяявляется горизонтальной асимптотой графикаприили, если

или

соответственно.

        Пример 7.6Рассмотрим функцию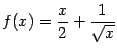. График этой функции имеет наклонную асимптотупри. Действительно,

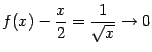при

Однако эта функция не определена ни на каком луче вида , так что её график не может иметь асимптоты при.

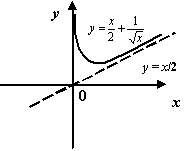
Рис.7.7.Наклонная асимптота функции

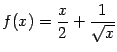
        Пример 7.7График функции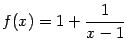имеет горизонтальную асимптотукак при, так и при, поскольку, очевидно,при. Можно сказать также, что асимптота приу этого графика совпадает с асимптотой при.

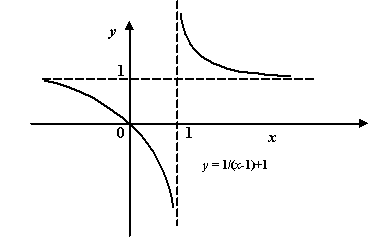
Рис.7.8.Горизонтальная асимптота функции

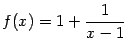
Аналогично определению наклонной асимптоты можно дать также более общее определение:

        Определение 7.3Линияназываетсяасимптотической линиейграфика функциипри(или при), если обе эти функции определены на некотором луче(или луче) и разность ординат графиков стремится к 0 при(или при, соответственно).

Если функция -- линейная, то есть график-- наклонная прямая, то асимптотическая линия -- это наклонная асимптота. Однако и другие линии бывает естественно рассматривать в качестве асимптотических.

        Пример 7.8Рассмотрим функцию. Приграфик этой функции имеет асимптотическую линию, поскольку разность междуи, равная, очевидно,, стремится к 0 при.

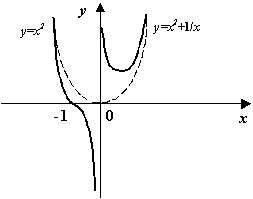
Рис.7.9.Асимптотическая линия графика функции

        Замечание 7.1Функцииивходят в определение асимптотической линии симметрично: если график-- асимптотическая линия для графика, то и-- асимптотическая линия для. На практике, однако, естественно считать асимптотической линией тот из двух графиков, который задаётся более простой формулой и вид которого известен.

        Пример 7.9Рассмотрим функцию. Так какпри, то естественно рассматривать графиккак асимптотическую линию придля графика исследуемой функции.

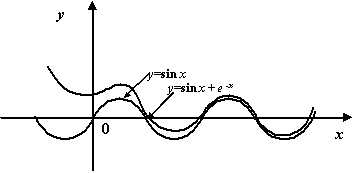
Рис.7.10.Асимптотическая линия для графика функциипри

Вернёмся к наклонным асимптотам -- прямым линиям с уравнением . Для их нахождения в тех случаях, когда значенияине очевидны, можно применять следующую теорему.

Теорема 7.1Прямая служит наклонной асимптотой для графикапри(или при) в том и только том случае, когда

(7.2)

и

(7.3)

(соответственно, есл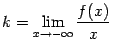и

и

Таким образом, для нахождения наклонной (или горизонтальной, если получится ) асимптоты достаточно найти два указанных пределаи, затем,. Прямаябудет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.

        Доказательствотеоремы.     Докажем теорему в случае; доказательство припроводится совершенно аналогично.

Перепишем условие (7.1), задающее асимптоту, в виде

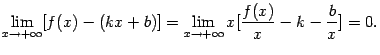
Так как первый множитель , то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть

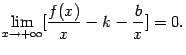
Но 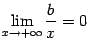и, так что

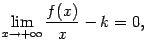
откуда следует равенство (7.2). Теперь числоуже известно.

Подставляя это число в формулу (7.1), находим, что

откуда следует равенство (7.3).

        Пример 7.10Найдём наклонные асимптоты графика.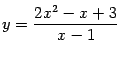

Попробуем отыскивать сразу оба предела, и при , и при.

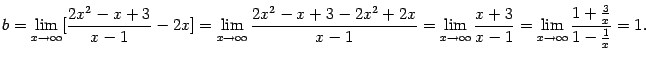
Итак, и при , и приимееми, так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение, то есть, фактически, асимптота только одна.

Рис.7.11.График 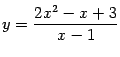и его наклонная асимптота

        Замечание 7.2Из определения асимптоты не следует, что если асимптоты прии придля одного и того же графика существуют, то они непременно совпадают. Это могут быть и различные прямые, как показывает следующий простой пример.

        Пример 7.11Рассмотрим график. Приграфик приближается к горизонтальной асимптоте, а при-- к другой горизонтальной асимптоте.

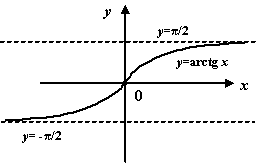
Рис.7.12.График арктангенса имеет две разных горизонтальных асимптоты

Различными могут оказаться и не обязательно горизонтальные асимптоты:

        Пример 7.12Рассмотрим функцию. Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.

Сначала найдём асимптоту при. Согласно доказанной теореме, имеем:

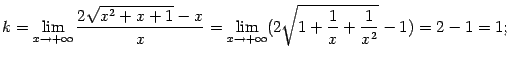
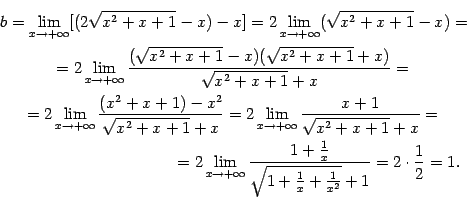
Таким образом, при наклонной асимптотой служит прямая.

Теперь найдём асимптоту при . Имеем:

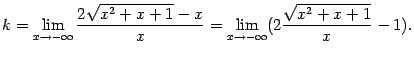
Поскольку , мы можем считать, что в допредельном выражении. В полученной дроби поделим числитель и знаменатель на положительное число. Тогда под корнем нужно будет поделить на, и получится:

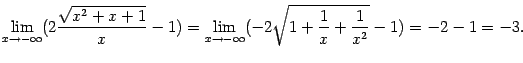
Вычисление проведите сами в качестве упражнения. При этом получается, так что наклонная асимптота приимеет уравнение.

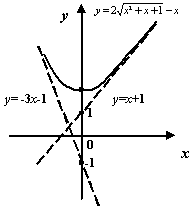
Рис.7.13.График и его две наклонных асимптоты

        Замечание 7.3Если графикимеет асимптоту(например, при) и существует предел производной:

то. Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты¹⁷.

Однако асимптота может существовать и в случае, когда производная не имеет никакого предела при. Дело в том, что значениямогут совершать мелкие, но частые колебания относительно ординаты асимптоты, так что значения производной могут при этом испытывать незатухающие колебания. Проиллюстрируем эту возможность следующим примером.

        Пример 7.13Рассмотрим функцию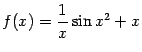. Очевидно, что прямая-- это асимптота графикапри, так как первое слагаемое имеет предел, равный 0, при. Однако вычисление производной даёт

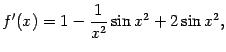
а эта функция при росте совершает колебания, причём при большихвторое слагаемое становится пренебрежимо малым, и значенияколеблются примерно междуи 3. Следовательно, производная не имеет предела при.

Если же рассмотреть функцию 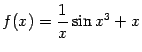, то её производная оказывается даже неограниченной на любом луче вида

Возрастание и убывание функции

Возрастание и убывание дифференцируемой функции связано со знаком её производной. Напомним, что функция называетсявозрастающейна интервале , если для любых двух точек из неравенства следует, что ;убывающейна интервале , если из неравенства следует, что ;невозрастающейна интервале , если из неравенства следует, что , инеубывающейна интервале , если из неравенства следует, что .

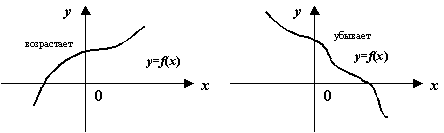
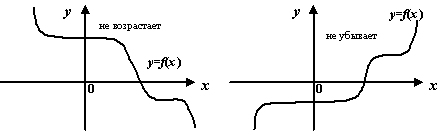
Рис.7.15.Графики возрастающей, убывающей, невозрастающей и неубывающей функцийCLX.ru - реклама в интернет

Очевидно, что функция возрастает тогда и только тогда, когда убывает функция ; аналогичное утверждение связывает неубывающую функцию с невозрастающей.

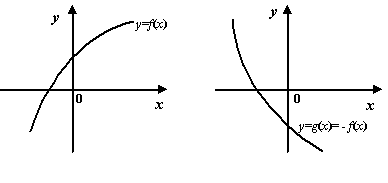
Рис.7.16.Графики функций и

Теорема 7.2Пусть функция дифференцируема на интервале и при всех . Тогда возрастает на . Если же при всех , то не убывает на .

Аналогично, если при всех , то убывает на , а если при всех , то не возрастает на .

 

        Доказательство.     В силу предыдущего замечания, теорему достаточно доказывать только для случаев и . Пусть при всех и , . Применим к отрезку формулу конечных приращений:

 

 

где . В правой части и , так что , откуда , что означает возрастание функции.

Точно так же, если , то получаем , откуда , что означает неубывание функции.

Имеет место и утверждение, "почти обратное" к предыдущей теореме:

        Теорема 7.3Если дифференцируемая функция не убывает на интервале , то при всех ; если же функция не возрастает на , то при .

 

        Доказательство.     Фиксируем точку и рассмотрим предел, который равен производной:

 

 

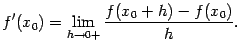
При достаточно малых точка попадёт в интервал , при этом , откуда . Значит, числитель неотрицателен, а знаменатель положителен, и дробь неотрицательна. По теореме о переходе к пределу в неравенстве, получаем , что и требовалось получить.

Вторая часть утверждения теоремы доказывается аналогично.     

Заметим, что усилить утверждение теоремы нельзя: из того, что функция возрастает на не следует строгого неравенства для производной. Действительно, в этом нас убеждает простой пример:

        Пример 7.15Рассмотрим функцию . Эта функция дифференцируема всюду и возрастает на всей оси : из следует, что . Однако неверно, что при всех : действительно, производная обращается в 0 при .

 

Итак, всё, что мы можем гарантировать в случае строгого возрастания (как и в случае нестрогого возрастания, то есть неубывания) -- это нестрогое неравенство .

Практический смысл полученных утверждений о связи возрастания и убывания со знаком производной -- в том, что для того, чтобы найти интервалы возрастания функции , надо решить относительно неравенство , а чтобы найти интервалы убывания -- решить неравенство .

        Пример 7.16Рассмотрим функцию . Её производная такова:

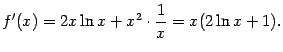
Интервал возрастания функции можно найти из неравенства

При решении этого неравенства учтём, что в области определения функции , так что нужно решать неравенство . Отсюда 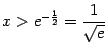. Таким образом, функция возрастает на интервале 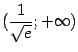. Нетрудно видеть, что при 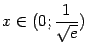выполняется обратное неравенство , так что на этом интервале функция убывает.

 

Рис.7.17.График функции

Если два интервала возрастания функции примыкают друг к другу, то есть имеют вид и , и функция непрерывна в точке , то эти два смежных интервала можно объединить: функция будет возрастать на . То же, разумеется, относится и к смежным интервалам убывания функции.

Рис.7.18.Объединение двух смежных интервалов возрастания функции

        Пример 7.17Рассмотрим функцию . Её производная имеет вид

Решая неравенство , получаем: ; при функция, очевидно, непрерывна, так что возрастает на объединённом интервале, то есть при . Решение неравенства даёт только один интервал ; на нём функция убывает.

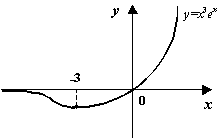
Рис.7.19.График функции

Геометрический смысл связи знака производной с направлением изменения функции легко виден из геометрического смысла производной: если угловой коэффициент касательной к графику (равный производной) положителен, то угол наклона касательной -- острый, что соответствует графику возрастающей функции. Если же угловой коэффициент отрицателен, то угол наклона касательной -- тупой, и тогда функция убывает.

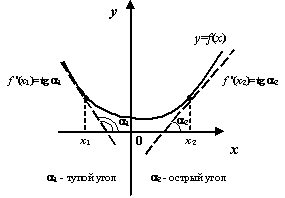
Рис.7.20.Связь угла наклона касательной с направлением изменения функции

Экстремум функции и необходимое условие экстремума

Напомним определение локального экстремума функции.

        Определение 7.4Пусть функция определена в некоторой окрестности , , некоторой точки своей области определения. Точка называетсяточкой локального максимума, если в некоторой такой окрестности выполняется неравенство (), иточкой локального минимума, если .

Понятия локальный максимумилокальный минимумобъединяются терминомлокальный экстремум.

Следующая теорема даёт необходимое условиетого, чтобы точка была точкой локального экстремума функции .

        Теорема 7.4Если точка  -- это точка локального экстремума функции , и существует производная в этой точке , то .

Доказательствоэтой теоремы сразу же следует из теоремы Ферма (см. гл. 5).

Утверждение теоремы можно переформулировать так:

если функция имеет локальный экстремум в точке , то либо 1) , либо 2) производная не существует.

CLX.ru - реклама в интернет

Точка называетсякритической точкойфункции , если непрерывна в этой точке и либо , либо не существует. В первом случае (то есть при ) точка называется такжестационарной точкойфункции .

Итак, локальный экстремум функции может наблюдаться лишь в одной из критических точек этой функции.

        Пример 7.18Рассмотрим функцию . Её производная существует при всех и равна . Следовательно, все критические точки -- стационарные и задаются уравнением . Это уравнение можно записать в виде ; оно имеет единственный корень : это единственная стационарная точка. Записав функцию в виде , легко увидеть, что в стационарной точке функция имеет минимум, равный .

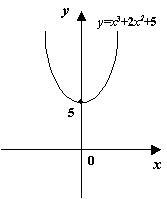
Рис.7.21.График функции

        Пример 7.19Рассмотрим функцию . Как и в предыдущем примере, производная существует при всех ; она равна . Все критические точки функции -- стационарные; таких точек три: .

Записав функцию в виде , легко увидеть, что в точках функция имеет минимум, так как в этих точках выражение обращается в 0, и

Если же мы запишем функцию в виде , то убедимся, что точка -- точка локального максимума, поскольку при малых выражение положительно, и

    

Рис.7.22.График функции

        Пример 7.20Рассмотрим функцию . Производная этой функции существует при всех , кроме : при и ; при и . Значит, единственная критическая точка -- та, в которой производная не существует, то есть . В этой точке, как легко видеть, имеет минимум.

        Пример 7.21Рассмотрим функцию

Заметим, что функция непрерывна при всех . Её производная равна

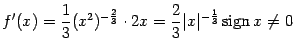
при и не существует при . Значит, единственная критическая точка функции -- это . Поскольку при и , то -- точка минимума.

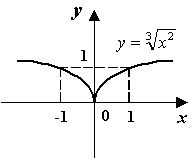
Рис.7.23.График функции

Не следует думать, что любая критическая точка функции даёт либо локальный максимум, либо локальный минимум. В некоторых критических точках экстремума может не оказаться вовсе.

        Пример 7.22Рассмотрим функцию . Её производная равна

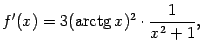
она существует при всех . Уравнение имеет решение -- это единственная критическая точка функции . Однако не является точкой локального экстремума, поскольку при всех и при всех .

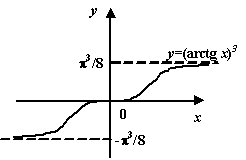
Рис.7.24.График функции

Пусть требуется отыскать максимальное и минимальное значения функции , непрерывной на замкнутом отрезке . Согласно сказанному выше, если точка экстремума (максимума либо минимума) -- это внутренняя точка отрезка, то эта точка обязана быть критической. Следовательно, точка экстремума на -- это либо критическая точка, либо один из концов отрезка.

Отсюда следует такой способ поиска максимума и минимума функции на : надо найти список "подозрительных" точек, включив в него: а) концы отрезка, то есть точки и ; б) стационарные точки, то есть все решения уравнения ; в) критические точки, не являющиеся стационарными, то есть те точки отрезка, в которых функция непрерывна, но производная не существует. Как правило, в этот список "подозрительных" точек входит конечное число точек. Во всех этих точках можно вычислить значение функции; максимальное и минимальное значение функции на отрезке будут содержаться в этом наборе значений, и их можно будет легко отыскать, а заодно установить и те значения , при которых эти экстремальные значения достигаются.

        Пример 7.23Найдём наибольшее и наименьшее значения функции

на отрезке .

Имеем: . Производная существует при всех , так что все критические точки функции являются стационарными, а стационарные точки задаются уравнением . Это квадратное уравнение имеет корни и ; первый корень не попадает на расматриваемый отрезок , а второй попадает. Поэтому список "подозрительных" точек таков: (оба конца отрезка и стационарная точка).

Вычисляем значения функции во всех точках списка:

Поэтому