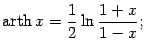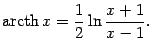- •Функции и их графики Конспекты, лекции, задачи
- •Первый способ задания функции: табличный
- •Clx.Ru - реклама в интернет
- •Упражнения
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
- •Сводка основных результатов о производных
- •Формула Тейлора теория и практика в примерах Многочлен Тейлора
- •Исследование функций и построение графиков Асимптоты графика функции
- •Достаточные условия локального экстремума
- •Примеры исследования функций и построения графиков
Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
Мы повторим здесь определение непрерывности функции, данное выше, в главе о пределах.
Определение 3.1Пусть
функция
![]() определена
на некотором интервале
определена
на некотором интервале
![]() ,
для которого
,
для которого
![]() --
внутренняя точка. Функция
--
внутренняя точка. Функция
![]() называетсянепрерывной в точке
называетсянепрерывной в точке
![]() ,
если существует предел
,
если существует предел
![]() при
при
![]() и
этот предел равен значению
и
этот предел равен значению
![]() ,
то есть
,
то есть
![]()
Пусть функция
![]() определена
на некотором полуинтервале
определена
на некотором полуинтервале
![]() ,
для которого
,
для которого
![]() --
левый конец. Функция
--
левый конец. Функция
![]() называетсянепрерывной справа в точке
называетсянепрерывной справа в точке
![]() ,
если существует предел
,
если существует предел
![]() при
при
![]() и
этот предел равен значению
и
этот предел равен значению
![]() ,
то есть
,
то есть
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пусть, наконец, функция
![]() определена
на некотором полуинтервале
определена
на некотором полуинтервале
![]() ,
для которого
,
для которого
![]() --
правый конец. Функция
--
правый конец. Функция
![]() называетсянепрерывной слева в точке
называетсянепрерывной слева в точке
![]() ,
если существует предел
,
если существует предел
![]() при
при
![]() и
этот предел равен значению
и
этот предел равен значению
![]() ,
то есть
,
то есть
![]()
Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.
Предложение 3.1Функция
![]() тогда
и только тогда непрерывна в точке
тогда
и только тогда непрерывна в точке
![]() ,
когда она непрерывна в точке
,
когда она непрерывна в точке
![]() справа
и слева, то есть когда выполнены следующие
условия:
справа
и слева, то есть когда выполнены следующие
условия:
1) функция
![]() определена
в точке
определена
в точке
![]() и
в некоторой окрестности этой точки;
и
в некоторой окрестности этой точки;
2) существует предел значений функции
слева:
![]() ;
;
3) существует предел значений функции
справа:
![]() ;
;
4) эти два предела совпадают между
собой и со значением функции в точке
![]() :
:
![]() .
.
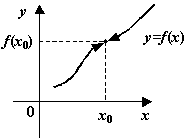
Рис.3.1.Функция
непрерывна: пределы слева и справа
совпадают с
![]()
Точка
![]() ,
в которой функция непрерывна, называетсяточкой непрерывностифункции
,
в которой функция непрерывна, называетсяточкой непрерывностифункции
![]() ;
так же определяются точки непрерывности
слева и справа.
;
так же определяются точки непрерывности
слева и справа.
Пример 3.1Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
Эти значения совпадают, значит, функция
.
Эти значения совпадают, значит, функция
![]() непрерывна
в точке
непрерывна
в точке
![]() .
.
(Функция
![]() --
элементарная функция;
--
элементарная функция;
![]() --
точка её области определения . Все
элементарные функции непрерывны во
всех внутренних точках своих областей
определения, в том числе и эта. Так что
в этом примере можно было бы заменить
--
точка её области определения . Все
элементарные функции непрерывны во
всех внутренних точках своих областей
определения, в том числе и эта. Так что
в этом примере можно было бы заменить
![]()
![]() любой
элементарной функцией, а
любой
элементарной функцией, а
![]() --
любой внутренней точкой области
--
любой внутренней точкой области
![]() ,
и вывод остался бы тем же.)
,
и вывод остался бы тем же.)
Пример 3.2Рассмотрим
функцию
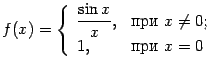 и
точку
и
точку
![]() .
При
.
При
![]() функция
задаётся формулой
функция
задаётся формулой
 ,
при этом имеем
,
при этом имеем
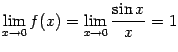 (первый
замечательный предел). Это значение
совпадает с тем, которое задано при
(первый
замечательный предел). Это значение
совпадает с тем, которое задано при
![]() :
:
![]() .
Итак,
.
Итак,
![]() ,
что означает непрервыность функции
,
что означает непрервыность функции
![]() при
при
![]() .
.
Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:
Предложение 3.2Пусть
![]() --
база непроколотых окрестностей
точки
--
база непроколотых окрестностей
точки
![]() ,
окончаниями которой служат интервалы
,
окончаниями которой служат интервалы
![]() ,
,
![]() ;
;
![]() --
база непроколотых левых окрестностей
точки
--
база непроколотых левых окрестностей
точки
![]() ,
окончаниями которой служат полуинтервалы
,
окончаниями которой служат полуинтервалы
![]() ,
,
![]() ;
;
![]() --
база непроколотых правых окрестностей
точки
--
база непроколотых правых окрестностей
точки
![]() ,
окончаниями которой служат полуинтервалы
,
окончаниями которой служат полуинтервалы
![]() ,
,
![]() .
Тогда непрерывность функции
.
Тогда непрерывность функции
![]() в
точке
в
точке
![]() эквивалентна
тому, что существует предел
эквивалентна
тому, что существует предел
![]() ;
непрерывность слева в точке
;
непрерывность слева в точке
![]() --
тому, что существует предел
--
тому, что существует предел
![]() ;
непрерывность справа в точке
;
непрерывность справа в точке
![]() --
тому, что существует предел
--
тому, что существует предел
![]() .
.
Определение точек разрыва
Дадим теперь определение точек разрыва функции.
Определение
3.2Точка
![]() называетсяточкой разрывафункции
называетсяточкой разрывафункции
![]() ,
если она определена в некоторой проколотой
окрестности точки
,
если она определена в некоторой проколотой
окрестности точки
![]() (то
есть определена на некотором интервале,
для которого
(то
есть определена на некотором интервале,
для которого
![]() служит
внутренней точкой, но в самой точке
служит
внутренней точкой, но в самой точке
![]() ,
возможно, не определена) и выполняется
хотя бы одно из следующих условий:
,
возможно, не определена) и выполняется
хотя бы одно из следующих условий:
1) не существует предела слева
![]() ;
;
2) не существует предела справа
![]() ;
;
3) пределы слева
![]() и
справа
и
справа
![]() существуют,
но не равны друг другу:
существуют,
но не равны друг другу:
![]() ;
;
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
4) пределы слева
![]() и
справа
и
справа
![]() существуют
и равны друг другу:
существуют
и равны друг другу:
![]() ,
но не совпадают со значением функции в
точке
,
но не совпадают со значением функции в
точке
![]() :
:
![]() ,
или функция
,
или функция
![]() не
определена в точке
не
определена в точке
![]() .
.
Если имеет место либо случай 3, либо
случай 4, то точка разрыва
![]() называетсяточкой разрыва первого рода, а
поведение функции в окрестности точки
называетсяточкой разрыва первого рода, а
поведение функции в окрестности точки
![]() называетсяразрывом первого родав точке
называетсяразрывом первого родав точке
![]() ;
в случае 4 точка разрыва первого рода
называетсяустранимой точкой разрыва,
а разрыв функции в этой точке --устранимым разрывом.
;
в случае 4 точка разрыва первого рода
называетсяустранимой точкой разрыва,
а разрыв функции в этой точке --устранимым разрывом.
Если же имеет место либо случай 1, либо
случай 2 (либо и тот и другой сразу), то
точка разрыва
![]() называетсяточкой разрыва второго рода, а
поведение функции в окрестности этой
точки --разрывом второго родав
точке
называетсяточкой разрыва второго рода, а
поведение функции в окрестности этой
точки --разрывом второго родав
точке
![]() .
.
Итак, если функция
![]() имеет
разрыв первого рода в точке
имеет
разрыв первого рода в точке
![]() ,
то существуют, как часто говорят, значения
функции "на берегах разрыва":
,
то существуют, как часто говорят, значения
функции "на берегах разрыва":
![]() и
и
![]() ,
но точка
,
но точка
![]() не
является точкой непрерывности.
не
является точкой непрерывности.
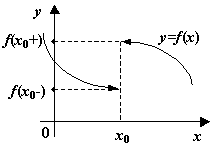
Рис.3.2.![]() --
точка разрыва первого рода
--
точка разрыва первого рода
Если значения на берегах разрыва разные,
то значение функции в точке
![]() может
быть любым (или вообще отсутствовать),
всё равно
может
быть любым (или вообще отсутствовать),
всё равно
![]() будет
давать разрыв первого рода. Если же
значения на берегах разрыва совпадают,
то для наличия разрыва нужно, чтобы либо
эти совпадающие значения были отличны
от значения функции в точке
будет
давать разрыв первого рода. Если же
значения на берегах разрыва совпадают,
то для наличия разрыва нужно, чтобы либо
эти совпадающие значения были отличны
от значения функции в точке
![]() ,
либо функция в этой точке была вовсе не
определена. Если в этом случае
переопределить (или доопределить)
функцию
,
либо функция в этой точке была вовсе не
определена. Если в этом случае
переопределить (или доопределить)
функцию
![]() в
точке
в
точке
![]() ,
положив
,
положив
![]() ,
то полученная изменённая функция будет
уже непрерывна в точке
,
то полученная изменённая функция будет
уже непрерывна в точке
![]() и
разрыв в точке
и
разрыв в точке
![]() исчезнет;
отсюда и название такого разрыва --
устранимый.
исчезнет;
отсюда и название такого разрыва --
устранимый.
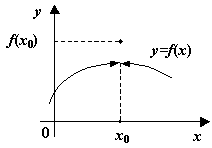
Рис.3.3.![]() --
точка устранимого разрыва
--
точка устранимого разрыва
Наконец, к разрывам второго рода, как
видно из определения, относятся все
разрывы, которые не принадлежат к
разрывам первого рода; некоторые из
возможных способов поведения функции
в окрестности точки
![]() ,
где происходит разрыв второго рода,
представлены на следующем рисунке.
,
где происходит разрыв второго рода,
представлены на следующем рисунке.
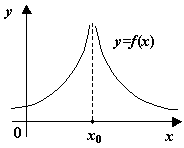
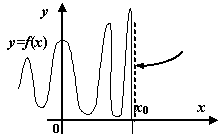

Рис.3.4.![]() --
точка разрыва второго рода. Некоторые
возможные варианты
--
точка разрыва второго рода. Некоторые
возможные варианты![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример 3.3Рассмотрим функцию
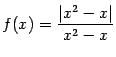 ,
для которой
,
для которой
![]()
Функция имеет разрывы при
![]() и
при
и
при
![]() .
Нетрудно видеть, что при
.
Нетрудно видеть, что при
![]()
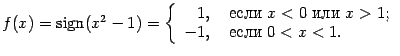 В
точках
В
точках
![]() и
и
![]() функция
имеет неустранимые разрывы первого
рода. В точке
функция
имеет неустранимые разрывы первого
рода. В точке
![]() имеем:
имеем:
![]()
(значения на краях разыва существуют,
но не совпадают); в точке
![]() --
--
![]()
(снова пределы слева и справа существуют, но не совпадают).
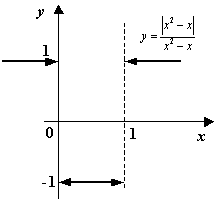
Рис.3.5.График
функции
![]()
Пример 3.4Функция
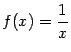 имеет
при
имеет
при
![]() разрыв
второго рода, так как
разрыв
второго рода, так как
![]() при
при
![]() и
и
![]() при
при
![]() .
.
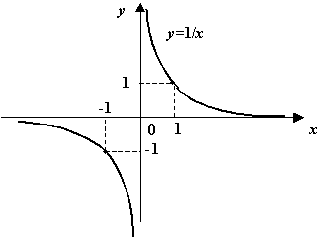
Рис.3.6.График
функции
![]()
Пример 3.5Функция
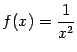 имеет
при
имеет
при
![]() разрыв
второго рода, так как
разрыв
второго рода, так как
![]() при
при
![]() и
при
и
при
![]() .
.

Рис.3.7.График
функции
![]()
Пример 3.6Возьмём
![]() .
Все точки области определения
.
Все точки области определения
![]() этой
элементарной функции являются точками
непрерывности. Поскольку
этой
элементарной функции являются точками
непрерывности. Поскольку
![]() не
входит в область определения функции
не
входит в область определения функции
![]() ,
но
,
но
![]() определена
во всех точках любой проколотой
окрестности 0, то 0 -- точка разрыва
функции
определена
во всех точках любой проколотой
окрестности 0, то 0 -- точка разрыва
функции
![]() .
Разобранный выше пример 3.2 показывает,
что если доопределить эту функцию при
.
Разобранный выше пример 3.2 показывает,
что если доопределить эту функцию при
![]() ,
положив
,
положив
![]() ,
то функция становится непрерывной в
точке 0. Значит, 0 -- точка разрыва
первого рода для функции
,
то функция становится непрерывной в
точке 0. Значит, 0 -- точка разрыва
первого рода для функции
![]() .
.
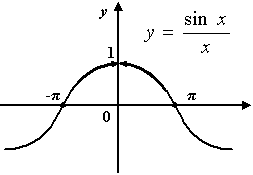
Рис.3.8.Устранимый
разрыв функции
![]()
Пример 3.7Рассмотрим функцию
![]() .
Её область определения
.
Её область определения
![]() состоит
из точек непрерывности, так как это
элементарная функция. Точка
состоит
из точек непрерывности, так как это
элементарная функция. Точка
![]() ,
в которой функция не определена, --
это точка разрыва функции. Поскольку
,
в которой функция не определена, --
это точка разрыва функции. Поскольку
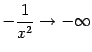 при
при
![]() ,
то
,
то
![]() .
Это означает, что при
.
Это означает, что при
![]() функция
имеет устранимый разрыв и становится
непрерывной на всей вещественной оси,
если положить
функция
имеет устранимый разрыв и становится
непрерывной на всей вещественной оси,
если положить
![]() .
.
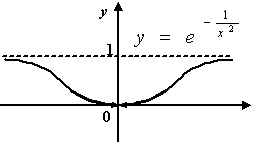
Рис.3.9.Устранимый
разрыв функции
![]()
Пример 3.8Рассмотрим функцию
![]() ,
где
,
где
![]() .
При
.
При
![]() она
имеет разрыв, так как
она
имеет разрыв, так как
![]() .
Поскольку
.
Поскольку
![]() --
ограниченная функция, а
--
ограниченная функция, а
![]() при
при
![]() ,
то
,
то
![]() (по
теореме 2.7). Следовательно, разрыв
устранимый, и если доопределить функцию,
положив
(по
теореме 2.7). Следовательно, разрыв
устранимый, и если доопределить функцию,
положив
![]() ,
она становится непрерывной при всех
,
она становится непрерывной при всех
![]() .
.
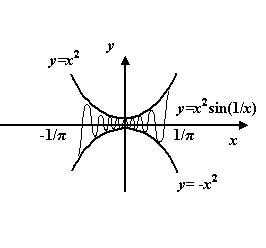
Рис.3.10.График
функции
![]() при
при
![]()
Пример 3.9Рассмотрим функцию
![]() ,
заданную равенством
,
заданную равенством
![]()
При
![]() ,
,
![]() ,
,
![]() ,
так что последовательность
,
так что последовательность
![]() --
это геометрическая прогрессия со
знаменателем
--
это геометрическая прогрессия со
знаменателем
![]() ,
,
![]() ,
и
,
и
![]() При
При
![]() ,
,
![]() ,
,
![]() ,
и все
,
и все
![]() ,
так что
,
так что
![]() При
При
![]() ,
,
![]() ,
,
![]() ,
и последовательность имеет вид
,
и последовательность имеет вид
![]()
Эта последовательность предела не
имеет, так что функция
![]() не
определена при
не
определена при
![]() ,
,
![]() .
.
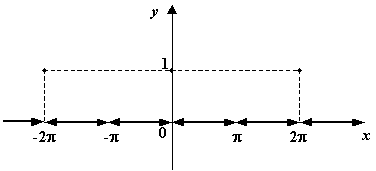
Рис.3.11.График
функции
![]()
Получаем, что
![]() .
Точками разрыва этой функции служат
как все точки, не принадлежащие области
определения (точки вида
.
Точками разрыва этой функции служат
как все точки, не принадлежащие области
определения (точки вида
![]() ,
,
![]() ),
так и все точки вида
),
так и все точки вида
![]() ,
,
![]() ,
в которых функция принимает значение 1.
Все точки разрыва -- устранимые, так
как пределы функции слева и справа в
этих точках совпадают и равны 0.
,
в которых функция принимает значение 1.
Все точки разрыва -- устранимые, так
как пределы функции слева и справа в
этих точках совпадают и равны 0.
Пример 3.10Рассмотрим функцию
![]() ;
её область определения
;
её область определения
![]() ,
и точка
,
и точка
![]() --
точка разрыва. Рассмотрим поведение
функции слева и справа от точки разрыва.
При
--
точка разрыва. Рассмотрим поведение
функции слева и справа от точки разрыва.
При
![]() будет
будет
![]() и
и
![]() ;
при
;
при
![]() будет
будет
![]() и
и
![]() .
Итак, значения "на правом берегу"
разрыва не существует, и разрыв функции
.
Итак, значения "на правом берегу"
разрыва не существует, и разрыв функции
![]() в
точке
в
точке
![]() --
второго рода.
--
второго рода.
Рис.3.12.График
функции
![]()
Замечание
3.1Если функция
![]() не
определена на интервале, примыкающем
к точке
не
определена на интервале, примыкающем
к точке
![]() слева
или справа, то точку
слева
или справа, то точку
![]() мы
не считаем точкой разрыва функции.
мы
не считаем точкой разрыва функции.
Пример 3.11Рассмотрим функцию
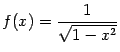 .
Её область определения --
.
Её область определения --
![]() .
При
.
При
![]() и
при
и
при
![]() знаменатель
знаменатель
![]() стремится
к 0 и положителен, так что
стремится
к 0 и положителен, так что
![]() .
однако точки
.
однако точки
![]() и
и
![]() мы
не считаем точками разрыва, так как
функция
мы
не считаем точками разрыва, так как
функция
![]() не
определена при
не
определена при
![]() и
при
и
при![]() .
.

Рис.3.13.График
функции
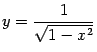
Пример 3.12Рассмотрим функцию
 .
Её область определения -- это
.
Её область определения -- это
![]() .
Точка
.
Точка
![]() не
является точкой разрыва функции
не
является точкой разрыва функции
![]() ,
несмотря на характер её поведения при
,
несмотря на характер её поведения при
![]() ,
поскольку функция
,
поскольку функция
![]() не
определена при
не
определена при
![]() .
.
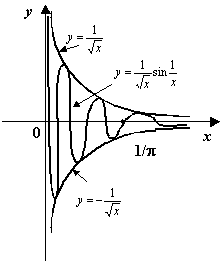
Рис.3.14.График
функции
Свойства функций, непрерывных в точке
Поскольку точки
![]() непрерывности
функции
непрерывности
функции
![]() задаются
условием
задаются
условием
![]() ,
то часть свойств функций, непрерывных
в точке
,
то часть свойств функций, непрерывных
в точке
![]() ,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы.
,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы.
Теорема 3.1Пусть функции
![]() и
и
![]() непрерывны
в точке
непрерывны
в точке
![]() .
Тогда функции
.
Тогда функции
![]() ,
,
![]() ,
,
![]() непрерывны
в точке
непрерывны
в точке
![]() .
Если
.
Если
![]() ,
то функция
,
то функция
 также
непрерывна в точке
также
непрерывна в точке
![]() .
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение
3.3Рассмотрим множество всех
функций, определённых в некоторой
фиксированной окрестности
![]() точки
точки
![]() и
непрерывных в этой точке. Тогда это
множество
и
непрерывных в этой точке. Тогда это
множество
![]() является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Доказательство.
Действительно, постоянные
![]() и
и
![]() --
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке
--
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке
![]() пpоизведения
пpоизведения
![]() и
и
![]() .
Но тогда по этой же теоpеме непpеpывна в
точке
.
Но тогда по этой же теоpеме непpеpывна в
точке
![]() и
сумма
и
сумма
![]() .
.
Теорема 3.2Пусть функции
![]() и
и
![]() таковы,
что существует композиция
таковы,
что существует композиция
![]() ,
,
![]() .
Пусть функция
.
Пусть функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
а функция
,
а функция
![]() непрерывна
в соответствующей точке
непрерывна
в соответствующей точке
![]() .
Тогда композиция
.
Тогда композиция
![]() непрерывна
в точке
непрерывна
в точке
![]() .
.
Доказательство.
Заметим, что равенство
![]() означает,
что при
означает,
что при
![]() будет
будет
![]() .
Значит,
.
Значит,
![]()
(последнее равенство следует из
непрерывности функции
![]() в
точке
в
точке
![]() ).
Значит,
).
Значит,
![]()
а это равенство означает, что композиция
![]() непрерывна
в точке
непрерывна
в точке
![]() .
.
Заметим, что, очевидно, в предыдущих
двух теоремах можно было бы заменить
базу
![]() на
односторонние базы
на
односторонние базы
![]() или
или
![]() и
получить аналогичные утверждения для
непрерывности слева или справа:
и
получить аналогичные утверждения для
непрерывности слева или справа:
Теорема 3.3Пусть функции
![]() и
и
![]() непрерывны
слева (справа) в точке
непрерывны
слева (справа) в точке
![]() .
Тогда функции
.
Тогда функции
![]() ,
,
![]() ,
,
![]() непрерывны
слева (соотв. справа) в точке
непрерывны
слева (соотв. справа) в точке
![]() .
Если
.
Если
![]() ,
то функция
,
то функция
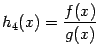 также
непрерывна слева (спpава) в точке
также
непрерывна слева (спpава) в точке
![]() .
.
Теорема 3.4Пусть функция
![]() непрерывна
слева (справа) в точке
непрерывна
слева (справа) в точке
![]() ,
а функция
,
а функция
![]() непрерывна
в точке
непрерывна
в точке
![]() .
Тогда композиция
.
Тогда композиция
![]() непрерывна
слева (соотв. справа) в точке
непрерывна
слева (соотв. справа) в точке
![]() .
.
Непрерывность функции на интервале и на отрезке
Определение
3.3Пусть
![]() --
некоторая функция,
--
некоторая функция,
![]() --
её область определения и
--
её область определения и
![]() --
некоторый (открытый) интервал (может
быть, с
--
некоторый (открытый) интервал (может
быть, с
![]() и/или
и/или
![]() ).
Назовём функцию
).
Назовём функцию
![]() непрерывной
на интервале
непрерывной
на интервале
![]() ,
если
,
если
![]() непрерывна
в любой точке
непрерывна
в любой точке
![]() ,
то есть для любого
,
то есть для любого
![]() существует
существует
![]() (в
сокращённой записи:
(в
сокращённой записи:![]()
Пусть теперь
![]() --
(замкнутый) отрезок в
--
(замкнутый) отрезок в
![]() .
Назовём функцию
.
Назовём функцию
![]() непрерывной
на отрезке
непрерывной
на отрезке
![]() ,
если
,
если
![]() непрерывна
на интервале
непрерывна
на интервале
![]() ,
непрерывна справа в точке
,
непрерывна справа в точке
![]() и
непрерывна слева в точке
и
непрерывна слева в точке
![]() ,
то есть
,
то есть![]()
![]()
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример 3.13Рассмотрим
функцию
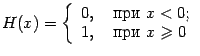 (функция
Хевисайда) на отрезке
(функция
Хевисайда) на отрезке
![]() ,
,
![]() .
Тогда
.
Тогда
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() (несмотря
на то, что в точке
(несмотря
на то, что в точке
![]() она
имеет разрыв первого рода).
она
имеет разрыв первого рода).
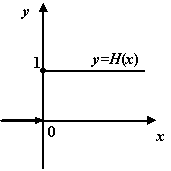
Рис.3.15.График функции Хевисайда
Аналогичное определение можно дать и
для полуинтервалов вида
![]() и
и
![]() ,
включая случаи
,
включая случаи
![]() и
и
![]() .
Однако можно обобщить данное определение
на случай произвольного подмножества
.
Однако можно обобщить данное определение
на случай произвольного подмножества
![]() следующим
образом. Введём сначала понятиеиндуцированнойна
следующим
образом. Введём сначала понятиеиндуцированнойна
![]() базы:
пусть
базы:
пусть
![]() --
база, все окончания
--
база, все окончания
![]() которой
имеют непустые пересечения с
которой
имеют непустые пересечения с
![]() .
Обозначим
.
Обозначим
![]() через
через
![]() и
рассмотрим множество всех
и
рассмотрим множество всех
![]() .
Нетрудно тогда проверить, что множество
.
Нетрудно тогда проверить, что множество
![]() будет
базой. Тем самым для
будет
базой. Тем самым для
![]() определены
базы
определены
базы
![]() ,
,
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() --
базы непроколотых двусторонних
(соответственно левых, правых) окрестностей
точки
--
базы непроколотых двусторонних
(соответственно левых, правых) окрестностей
точки
![]() (их
определение см. в начале текущей главы).
(их
определение см. в начале текущей главы).
Определение
3.4Назовём функцию
![]() непрерывной
на множестве
непрерывной
на множестве
![]() ,
если
,
если![]()
Нетрудно видеть, что тогда при
![]() и
при
и
при
![]() это
определение совпадает с теми, что были
выше даны специально для интервала и
отрезка.
это
определение совпадает с теми, что были
выше даны специально для интервала и
отрезка.
Напомним, что все элементарные функции непрерывны во всех точках своих областей определения и, следовательно, непрерывны на любых интервалах и отрезках, лежащих в их областях определения.
Поскольку непрерывность на интервале и отрезке определяется поточечно, имеет место теорема, которая является непосредственным следствием теоремы 3.1:
Теорема 3.5Пусть
![]() и
и
![]() --
функции и
--
функции и
![]() --
интервал или отрезок, лежащий в
--
интервал или отрезок, лежащий в
![]() .
Пусть
.
Пусть
![]() и
и
![]() непрерывны
на
непрерывны
на
![]() .
Тогда функции
.
Тогда функции
![]() ,
,
![]() ,
,
![]() непpеpывны
на
непpеpывны
на
![]() .
Если вдобавок
.
Если вдобавок
![]() пpи
всех
пpи
всех
![]() ,
то функция
,
то функция
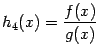 также
непpеpывна на
также
непpеpывна на
![]() .
.
Из этой теоpемы вытекает следующее утвеpждение, точно так же, как из теоpемы 3.1 -- пpедложение 3.3:
Предложение
3.4Множество
![]() всех
функций, непpеpывных на интеpвале или
отpезке
всех
функций, непpеpывных на интеpвале или
отpезке
![]() --
это линейное пpостpанство:
--
это линейное пpостpанство:
![]()
Более сложное свойство непрерывной функции выражает следующая теорема.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Теорема 3.6(о корне непрерывной функции)Пусть
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
причём
,
причём
![]() и
и
![]() --
числа разных знаков. (Будем для
определённости считать, что
--
числа разных знаков. (Будем для
определённости считать, что
![]() ,
а
,
а
![]() .)
Тогда существует хотя бы одно такое
значение
.)
Тогда существует хотя бы одно такое
значение
![]() ,
что
,
что
![]() (то
есть существует хотя бы один корень
(то
есть существует хотя бы один корень
![]() уравнения
уравнения
![]() ).
).
Доказательство.
Рассмотрим середину отрезка
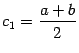 .
Тогда либо
.
Тогда либо
![]() ,
либо
,
либо
![]() ,
либо
,
либо
![]() .
В первом случае корень найден: это
.
В первом случае корень найден: это
![]() .
В остальных двух случаях рассмотрим ту
часть отрезка, на концах которой функция
.
В остальных двух случаях рассмотрим ту
часть отрезка, на концах которой функция
![]() принимает
значения разных знаков:
принимает
значения разных знаков:
![]() в
случае
в
случае
![]() или
или
![]() в
случае
в
случае
![]() .
Выбранную половину отрезка обозначим
через
.
Выбранную половину отрезка обозначим
через
![]() и
применим к ней ту же процедуру: разделим
на две половины
и
применим к ней ту же процедуру: разделим
на две половины
![]() и
и
![]() ,
где
,
где
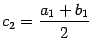 ,
и найдём
,
и найдём
![]() .
В случае
.
В случае
![]() корень
найден; в случае
корень
найден; в случае
![]() рассматриваем
далее отрезок
рассматриваем
далее отрезок
![]() ,
в случае
,
в случае
![]() --
отрезок
--
отрезок
![]() и
т. д.
и
т. д.
Получаем, что либо на некотором шаге
будет найден корень
![]() ,
либо будет построена система вложенных
отрезков
,
либо будет построена система вложенных
отрезков
![]()
в которой каждый следующий отрезок
вдвое короче предыдущего. Последовательность
![]() --
неубывающая и ограниченная сверху
(например, числом
--
неубывающая и ограниченная сверху
(например, числом
![]() );
следовательно (по теореме 2.13), она имеет
предел
);
следовательно (по теореме 2.13), она имеет
предел
![]() .
Последовательность
.
Последовательность
![]() --
невозрастающая и ограниченная снизу
(например, числом
--
невозрастающая и ограниченная снизу
(например, числом![]() );
значит, существует предел
);
значит, существует предел
![]() .
Поскольку длины отрезков
.
Поскольку длины отрезков
![]() образуют
убывающую геометрическую прогрессию
(со знаменателем
образуют
убывающую геометрическую прогрессию
(со знаменателем
![]() ),
то они стремятся к 0, и
),
то они стремятся к 0, и
![]() ,
то есть
,
то есть
![]() .
Положим теперь
.
Положим теперь
![]() .
Тогда
.
Тогда
![]() и
и![]()
поскольку функция
![]() непрерывна.
Однако, по построению последовательностей
непрерывна.
Однако, по построению последовательностей
![]() и
и
![]() ,
,
![]() и
и
![]() ,
так что, по теореме о переходе к пределу
в неравенстве (теорема 2.7),
,
так что, по теореме о переходе к пределу
в неравенстве (теорема 2.7),
![]() и
и
![]() ,
то есть
,
то есть
![]() и
и
![]() .
Значит,
.
Значит,
![]() ,
и
,
и
![]() --
корень уравнения
--
корень уравнения
![]() .
.
Пример 3.14Рассмотрим функцию
![]() на
отрезке
на
отрезке
![]() .
Поскольку
.
Поскольку
![]() и
и
![]() --
числа разных знаков, то функция
--
числа разных знаков, то функция
![]() обращается
в 0 в некоторой точке
обращается
в 0 в некоторой точке
![]() интервала
интервала
![]() .
Это означает, что уравнение
.
Это означает, что уравнение
![]() имеет
корень
имеет
корень
![]() .
.
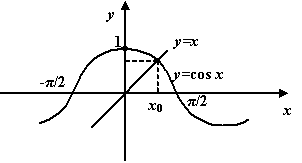
Рис.3.17.Графическое
представление корня уравнения
![]()
Доказанная теорема фактически даёт нам
способ нахождения корня
![]() ,
хотя бы приближённого, с любой заданной
наперёд степенью точности. Это --
метод деления отрезка пополам, описанный
при доказательстве теоремы. Более
подробно с этим и другими, более
эффективными, способами приближённого
нахождения корня мы познакомимся ниже,
после того, как изучим понятие и свойства
производной.
,
хотя бы приближённого, с любой заданной
наперёд степенью точности. Это --
метод деления отрезка пополам, описанный
при доказательстве теоремы. Более
подробно с этим и другими, более
эффективными, способами приближённого
нахождения корня мы познакомимся ниже,
после того, как изучим понятие и свойства
производной.
Заметим, что теорема не утверждает, что
если её условия выполнены, то корень
![]() --
единственный. Как показывает следующий
рисунок, корней может быть и больше
одного (на рисунке их 3).
--
единственный. Как показывает следующий
рисунок, корней может быть и больше
одного (на рисунке их 3).

Рис.3.18.Несколько корней функции, принимающей значения разных знаков в концах отрезка
Однако, если функция монотонно возрастает или монотонно убывает на отрезке, в концах которого принимает значения разных знаков, то корень -- единственный, так как строго монотонная функция каждое своё значение принимает ровно в одной точке, в том числе и значение 0.
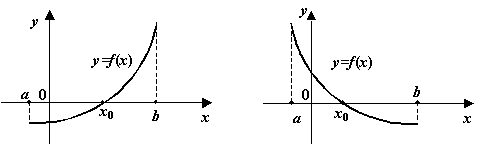
Рис.3.19.Монотонная функция не может иметь более одного корня
Непосредственным следствием теоремы о корне непрерывной функции является следующая теорема, которая и сама по себе имеет очень важное значение в математическом анализе.
Теорема 3.7(о промежуточном значении непрерывной
функции)Пусть функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и
и
![]() (будем
для определённости считать, что
(будем
для определённости считать, что
![]() ).
Пусть
).
Пусть
![]() --
некоторое число, лежащее между
--
некоторое число, лежащее между
![]() и
и
![]() .
Тогда существует такая точка
.
Тогда существует такая точка
![]() ,
что
,
что
![]() .
.

Рис.3.20.Непрерывная функция принимает любое промежуточное значение
Доказательство.
Рассмотрим вспомогательную функцию
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
Функция
.
Функция
![]() ,
очевидно, непрерывна, и по предыдущей
теореме существует такая точка
,
очевидно, непрерывна, и по предыдущей
теореме существует такая точка
![]() ,
что
,
что
![]() .
Но это равенство означает, что
.
Но это равенство означает, что
![]() .
.
Заметим, что если функция не является
непрерывной, то она может принимать не
все промежуточные значения. Например,
функция Хевисайда
![]() (см.
пример 3.13) принимает значения
(см.
пример 3.13) принимает значения
![]() ,
,
![]() ,
но нигде, в том числе и на интервале
,
но нигде, в том числе и на интервале
![]() ,
не принимает, скажем, промежуточного
значения
,
не принимает, скажем, промежуточного
значения
![]() .
Дело в том, что функция Хевисайда имеет
разрыв в точке
.
Дело в том, что функция Хевисайда имеет
разрыв в точке
![]() ,
лежащей как раз в интервале
,
лежащей как раз в интервале
![]() .
.
Для дальнейшего изучения свойств
функций, непрерывных на отрезке, нам
понадобится следующее тонкое свойство
системы вещественных чисел (мы уже
упоминали его в главе 2 в связи с теоремой
о пределе монотонно возрастающей
ограниченной функции): для любого
ограниченного снизу множества
![]() (то
есть такого, что
(то
есть такого, что
![]() при
всех
при
всех
![]() и
некотором
и
некотором
![]() ;
число
;
число
![]() называетсянижней граньюмножества
называетсянижней граньюмножества
![]() )
имеетсяточная нижняя грань
)
имеетсяточная нижняя грань
![]() ,
то есть наибольшее из чисел
,
то есть наибольшее из чисел
![]() ,
таких что
,
таких что
![]() при
всех
при
всех
![]() .
Аналогично, если множество
.
Аналогично, если множество
![]() ограничено
сверху, то оно имеетточную верхнюю
грань
ограничено
сверху, то оно имеетточную верхнюю
грань
![]() :
это наименьшая изверхних граней
:
это наименьшая изверхних граней
![]() (для
которых
(для
которых
![]() при
всех
при
всех
![]() ).
).

Рис.3.21.Нижняя и верхняя грани ограниченного множества
Если
![]() ,
то существует невозрастающая
последовательность точек
,
то существует невозрастающая
последовательность точек
![]() ,
которая стремится к
,
которая стремится к
![]() .
Точно так же если
.
Точно так же если
![]() ,
то существует неубывающая последовательность
точек
,
то существует неубывающая последовательность
точек
![]() ,
которая стремится к
,
которая стремится к
![]() .
.
Если точка
![]() принадлежит
множеству
принадлежит
множеству
![]() ,
то
,
то
![]() является
наименьшим элементом этого множества:
является
наименьшим элементом этого множества:
![]() ;
аналогично, если
;
аналогично, если
![]() ,
то
,
то
![]() .
.
Кроме того, для дальнейшего нам понадобится следующая
Лемма 3.1Пусть
![]() --
непрерывная функция на отрезке
--
непрерывная функция на отрезке
![]() ,
и множество
,
и множество
![]() тех
точек
тех
точек
![]() ,
в которых
,
в которых
![]() (или
(или
![]() ,
или
,
или
![]() )
не пусто. Тогда в множестве
)
не пусто. Тогда в множестве
![]() имеется
наименьшее значение
имеется
наименьшее значение
![]() ,
такое что
,
такое что
![]() при
всех
при
всех
![]() .
.
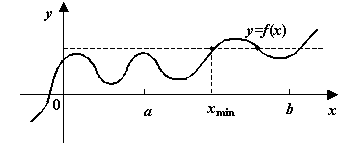
Рис.3.22.Наименьший аргумент, при котором функция принимает заданное значение
Доказательство.
Поскольку
![]() --
ограниченное множество (это часть
отрезка
--
ограниченное множество (это часть
отрезка
![]() ),
то оно имеет точную нижнюю грань
),
то оно имеет точную нижнюю грань
![]() .
Тогда существует невозрастающая
последовательность
.
Тогда существует невозрастающая
последовательность
![]() ,
,
![]() ,
такая что
,
такая что
![]() при
при
![]() .
При этом
.
При этом
![]() ,
по определению множества
,
по определению множества
![]() .
Поэтому, переходя к пределу, получаем,
с одной стороны,
.
Поэтому, переходя к пределу, получаем,
с одной стороны,
![]()
а с другой стороны, вследствие непрерывности
функции
![]() ,
,
![]()
Значит,
![]() ,
так что точка
,
так что точка
![]() принадлежит
множеству
принадлежит
множеству
![]() и
и
![]() .
.
В случае, когда множество
![]() задано
неравенством
задано
неравенством
![]() ,
мы имеем
,
мы имеем
![]() при
всех
при
всех
![]() и
по теореме о переходе к пределу в
неравенстве получаем
и
по теореме о переходе к пределу в
неравенстве получаем
![]()
откуда
![]() ,
что означает, что
,
что означает, что
![]() и
и
![]() .
Точно так же в случае неравенства
.
Точно так же в случае неравенства
![]() переход
к пределу в неравенстве даёт
переход
к пределу в неравенстве даёт
![]()
откуда
![]() ,
,
![]() и
и
![]() .
.
Теорема 3.8(об ограниченности непрерывной функции)Пусть функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() .
Тогда
.
Тогда
![]() ограничена
на
ограничена
на
![]() ,
то есть существует такая постоянная
,
то есть существует такая постоянная
![]() ,
что
,
что
![]() при
всех
при
всех
![]() .
.
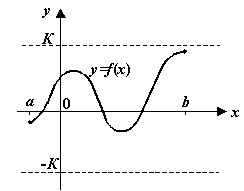
Рис.3.23.Непрерывная на отрезке функция ограничена
Доказательство.
Предположим обратное: пусть
![]() не
ограничена, например, сверху. Тогда все
множества
не
ограничена, например, сверху. Тогда все
множества
![]() ,
,
![]() ,
,
![]() ,
не пусты. По предыдущей лемме в каждом
из этих множеств
,
не пусты. По предыдущей лемме в каждом
из этих множеств
![]() имеется
наименьшее значение
имеется
наименьшее значение
![]() ,
,
![]() .
Покажем, что
.
Покажем, что
![]()
Действительно,
![]() .
Если какая-либо точка из
.
Если какая-либо точка из
![]() ,
например
,
например
![]() ,
лежит между
,
лежит между
![]() и
и
![]() ,
то
,
то
![]()
то есть
![]() --
промежуточное значение между
--
промежуточное значение между
![]() и
и
![]() .
Значит, по теореме о промежуточном
значении непрерывной функции, существует
точка
.
Значит, по теореме о промежуточном
значении непрерывной функции, существует
точка
![]() ,
такая что
,
такая что
![]() ,
и
,
и
![]() .
Но
.
Но
![]() ,
вопреки предположению о том, что
,
вопреки предположению о том, что
![]() --
наименьшее значение из множества
--
наименьшее значение из множества
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() при
всех
при
всех
![]() .
.
Точно так же далее доказывается, что
![]() при
всех
при
всех
![]() ,
,
![]() при
всех
при
всех
![]() ,
и т. д. Итак,
,
и т. д. Итак,
![]() --
возрастающая последовательность,
ограниченная сверху числом
--
возрастающая последовательность,
ограниченная сверху числом
![]() .
Поэтому существует
.
Поэтому существует
![]() .
Из непрерывности функции
.
Из непрерывности функции
![]() следует,
что существует
следует,
что существует
![]() ,
но
,
но
![]() при
при
![]() ,
так что предела не существует. Полученное
противоречие доказывает, что функция
,
так что предела не существует. Полученное
противоречие доказывает, что функция
![]() ограничена
сверху.
ограничена
сверху.
Аналогично доказывается, что
![]() ограничена
снизу, откуда следует утверждение
теоремы.
ограничена
снизу, откуда следует утверждение
теоремы.
Очевидно, что ослабить условия теоремы нельзя: если функция не является непрерывной, то она не обязана быть ограниченной на отрезке (приведём в качестве примера функцию
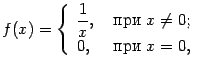
на отрезке
![]() .
Эта функция не ограничена на отрезке,
так как при
.
Эта функция не ограничена на отрезке,
так как при
![]() имеет
точку разрыва второго рода, такую что
имеет
точку разрыва второго рода, такую что
![]() при
при
![]() .
Также нельзя заменить в условии теоремы
отрезок интервалом или полуинтервалом:
в качестве примера рассмотрим ту же
функцию
.
Также нельзя заменить в условии теоремы
отрезок интервалом или полуинтервалом:
в качестве примера рассмотрим ту же
функцию
![]() на
полуинтервале
на
полуинтервале
![]() .
Функция непрерывна на этом полуинтервале,
но неограничена, вследствие того что
.
Функция непрерывна на этом полуинтервале,
но неограничена, вследствие того что
![]() при
при
![]() .
.
Поиск наилучших постоянных, которыми можно ограничить функцию сверху и снизу на заданном отрезке, естественным образом приводит нас к задаче об отыскании минимума и максимума непрерывной функции на этом отрезке. Возможность решения этой задачи описывается следующей теоремой.
Теорема 3.9(о достижении экстремума непрерывной
функцией)Пусть функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() .
Тогда существует точка
.
Тогда существует точка
![]() ,
такая что
,
такая что
![]() при
всех
при
всех
![]() (то
есть
(то
есть
![]() --
точка минимума:
--
точка минимума:
![]() ),
и существует точка
),
и существует точка
![]() ,
такая что
,
такая что
![]() при
всех
при
всех
![]() (то
есть
(то
есть
![]() --
точка максимума:
--
точка максимума:
![]() ).
Иными словами, минимальное и максимальное
значения непрерывной функции на отрезке
существуют и достигаются в некоторых
точках
).
Иными словами, минимальное и максимальное
значения непрерывной функции на отрезке
существуют и достигаются в некоторых
точках
![]() и
и
![]() этого
отрезка.
этого
отрезка.
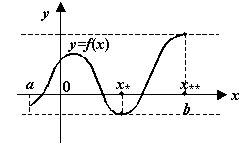
Рис.3.24.Непрерывная на отрезке функция достигает максимума и минимума
Доказательство.
Так как по предыдущей теореме функция
![]() ограничена
на
ограничена
на
![]() сверху,
то существует точная верхняя грань
значений функции на
сверху,
то существует точная верхняя грань
значений функции на
![]() --
число
--
число
![]() .
Тем самым, множества
.
Тем самым, множества
![]() ,
,
![]() ,...,
,...,
![]() ,...,
не пусты, и по предыдущей лемме в них
есть наименьшие значения
,...,
не пусты, и по предыдущей лемме в них
есть наименьшие значения
![]() :
:
![]() ,
,
![]() .
Эти
.
Эти
![]() не
убывают (доказывается это утверждение
точно так же, как в предыдущей теореме):
не
убывают (доказывается это утверждение
точно так же, как в предыдущей теореме):
![]()
и ограничены сверху числом
![]() .
Поэтому, по теореме о пределе монотонной
ограниченной последовательности,
существует предел
.
Поэтому, по теореме о пределе монотонной
ограниченной последовательности,
существует предел
![]() Так
как
Так
как
![]() ,
то и
,
то и
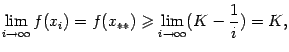
по теореме о переходе к пределу в
неравенстве, то есть
![]() .
Но при всех
.
Но при всех
![]()
![]() ,
и в том числе
,
и в том числе
![]() .
Отсюда получается, что
.
Отсюда получается, что
![]() ,
то есть максимум функции достигается
в точке
,
то есть максимум функции достигается
в точке
![]() .
.
Аналогично доказывается существование точки минимума.
В этой теореме, как и в предыдущей, нельзя ослабить условия: если функция не является непрерывной, то она может не достигать своего максимального или минимального значения на отрезке, даже будучи ограниченной. Для примера возьмём функцию
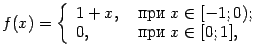
на отрезке
![]() .
Эта функция ограничена на отрезке
(очевидно, что
.
Эта функция ограничена на отрезке
(очевидно, что
![]() )
и
)
и
![]() ,
однако значение 1 она не принимает
ни в одной точке отрезка (заметим, что
,
однако значение 1 она не принимает
ни в одной точке отрезка (заметим, что
![]() ,
а не 1). Дело в том, что эта функция имеет
разрыв первого рода в точке
,
а не 1). Дело в том, что эта функция имеет
разрыв первого рода в точке
![]() ,
так что при
,
так что при
![]() предел
предел
![]() не
равен значению функции в точке 0.
Далее, непрерывная функция, заданная
на интервале или другом множестве, не
являющемся замкнутым отрезком (на
полуинтервале, полуоси) также может не
принимать экстремального значения. В
качестве примера рассмотрим функцию
не
равен значению функции в точке 0.
Далее, непрерывная функция, заданная
на интервале или другом множестве, не
являющемся замкнутым отрезком (на
полуинтервале, полуоси) также может не
принимать экстремального значения. В
качестве примера рассмотрим функцию
![]() на
интервале
на
интервале
![]() .
Очевидно, что функция непрерывна и что
.
Очевидно, что функция непрерывна и что
![]() и
и
![]() ,
однако ни значения 0, ни значения 1
функция не принимает ни в какой точке
интервала
,
однако ни значения 0, ни значения 1
функция не принимает ни в какой точке
интервала
![]() .
Рассмотрим также функцию
.
Рассмотрим также функцию
![]() на
полуоси
на
полуоси
![]() .
Эта функция непрерывна на
.
Эта функция непрерывна на
![]() ,
возрастает, принимает своё минимальное
значение 0 в точке
,
возрастает, принимает своё минимальное
значение 0 в точке
![]() ,
но не принимает ни в какой точке
максимального значения (хотя ограничена
сверху числом
,
но не принимает ни в какой точке
максимального значения (хотя ограничена
сверху числом
![]() и
и
![]()
Заметим, что доказанная теорема не даёт практического способа находить точки минимума и максимума функции на заданном отрезке. Такой способ мы обсудим позднее, когда изучим понятие производной. Однако теорема важна тем, что даёт нам уверенность в том, что искомый экстремум существует и мы сможем его отыскать
Равномерная непрерывность
Напомним, что непрерывность функции
![]() в
точке
в
точке
![]() означает,
что
означает,
что
![]() ,
то есть
,
то есть![]() Тем
самым непрерывность функции
Тем
самым непрерывность функции
![]() на
интервале или отрезке
на
интервале или отрезке
![]() означает,
что
означает,
что![]() При
этом мы имеем право выбирать число
При
этом мы имеем право выбирать число
![]() в
зависимости от
в
зависимости от
![]() и,
главное, от точки
и,
главное, от точки
![]() .
.
Предположим теперь, что число
![]() можно
выбрать общим для всех
можно
выбрать общим для всех
![]() (но,
конечно, зависящим от
(но,
конечно, зависящим от
![]() ).
Тогда говорят, что свойство функции
быть непрерывной в точке
).
Тогда говорят, что свойство функции
быть непрерывной в точке
![]() выполненоравномернопо
выполненоравномернопо
![]() .
.
Дадим теперь такое
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Определение
3.5Пусть
![]() --
некоторая функция и
--
некоторая функция и
![]() .
Функция
.
Функция
![]() равномерно
непрерывнана
равномерно
непрерывнана
![]() ,
если
,
если![]()
Приведём пример равномерно непрерывной функции.
Пример 3.15Рассмотрим функцию
![]() и
покажем, что она равномерно непрерывна
на всей числовой оси
и
покажем, что она равномерно непрерывна
на всей числовой оси
![]() .
Фиксируем число
.
Фиксируем число
![]() и
положим
и
положим
![]() .
Выберем теперь любые две точки
.
Выберем теперь любые две точки
![]() и
и
![]() ,
такие что
,
такие что
![]() ,
и покажем, что тогда
,
и покажем, что тогда
![]() .
Действительно,
.
Действительно,
|
|
|
так как, во-первых,
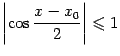 при
всех
при
всех
![]() и
и
![]() и,
во-вторых,
и,
во-вторых,
![]() при
всех
при
всех
![]() (у
нас
(у
нас
![]() ).
Таким образом. равномерная непрерывность
функции
).
Таким образом. равномерная непрерывность
функции
![]() доказана.
доказана.
Лучше изучить условие равномерности
по
![]() мы
сможем, приведя пример, где оно нарушается.
мы
сможем, приведя пример, где оно нарушается.
Пример 3.16Пусть функция
 рассматривается
на интервале
рассматривается
на интервале
![]() .
Если фиксирована точка
.
Если фиксирована точка
![]() ,
то для заданного
,
то для заданного
![]() мы
можем выбрать
мы
можем выбрать
![]() так,
что
так,
что
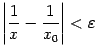 при
всех
при
всех
![]() таких,
что
таких,
что
![]() ;
для нахождения
;
для нахождения
![]() нужно
решить неравенство
нужно
решить неравенство
 относительно
относительно
![]() (напомним,
что точка
(напомним,
что точка
![]() фиксирована):
фиксирована):
|
|
|
|
|
|
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Из чисел
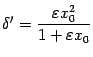 и
и
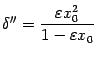 выберем
минимальное:
выберем
минимальное:
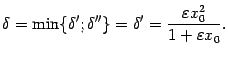
Тогда при
![]() будет
будет
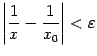 .
Проанализируем, однако, зависимость
.
Проанализируем, однако, зависимость
![]() от
от
![]() :
при
:
при
![]() ,
приближающемся к 0, значения
,
приближающемся к 0, значения
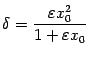 будут
убывать и стремиться к 0 (при неизменном
значении
будут
убывать и стремиться к 0 (при неизменном
значении
![]() ),
что хорошо видно на следующем чертеже:
),
что хорошо видно на следующем чертеже:
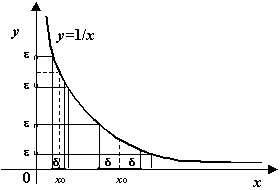
Рис.3.25.Изменение
![]() в
зависимости от положения точки
в
зависимости от положения точки
![]()
При приближении точки
![]() к
началу координат нам приходится по
одному и тому же
к
началу координат нам приходится по
одному и тому же
![]() выбирать
всё меньшие
выбирать
всё меньшие
![]() -окрестности
точки
-окрестности
точки
![]() ,
чтобы обеспечить выполнение неравенства
,
чтобы обеспечить выполнение неравенства
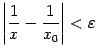 .
Выбрать
.
Выбрать
![]() общим
для всех
общим
для всех
![]() ,
очевидно, невозможно: при заданном
,
очевидно, невозможно: при заданном
![]() какое
бы фиксированное число
какое
бы фиксированное число
![]() ни
было взято, мы можем поместить точку
ни
было взято, мы можем поместить точку
![]() так
близко от 0, что значения
так
близко от 0, что значения
![]() и
и
![]() будут
отличаться друг от друга больше, чем на
будут
отличаться друг от друга больше, чем на
![]() ,
хотя
,
хотя
![]() .
Это означает, что функция не является
равномерно непрерывной на интервале
.
Это означает, что функция не является
равномерно непрерывной на интервале
![]() .
.
Теорема
3.10Пусть
![]() и
функция
и
функция
![]() непрерывна
на
непрерывна
на
![]() .
Тогда
.
Тогда
![]() равномерно
непрерывна на
равномерно
непрерывна на
![]() .
.
Доказательствоэтой теоремы
достаточно сложно и основывается на
тонких свойствах системы действительных
чисел, а именно, на том, что любой замкнутый
отрезок
![]() является
компактом Мы пропускаем здесь
доказательство теоремы, отсылая за ним
заинтересованного читателя к подробным
курсам математического анализа, например,Никольский С.М.,Курс математического
анализа, т. 1. -- М.: Наука, 1991;Фихтенгольц Г.М.,Курс дифференциального
и интегрального исчисления, т. 1. --
М.-Л.: ГИТТЛ, 1948 и др. годы изд.
является
компактом Мы пропускаем здесь
доказательство теоремы, отсылая за ним
заинтересованного читателя к подробным
курсам математического анализа, например,Никольский С.М.,Курс математического
анализа, т. 1. -- М.: Наука, 1991;Фихтенгольц Г.М.,Курс дифференциального
и интегрального исчисления, т. 1. --
М.-Л.: ГИТТЛ, 1948 и др. годы изд.
В качестве следствия равномерной непрерывности легко получается утверждение теоремы 3.8, а именно,
Следствие
3.1Любая функция
![]() ,
непрерывная на замкнутом отрезке
,
непрерывная на замкнутом отрезке
![]() ,
ограничена на
,
ограничена на
![]() (то
есть существует такое число
(то
есть существует такое число
![]() ,
что
,
что
![]() при
всех
при
всех
![]() ).
).
Приведём это доказательство (хотя теорема 3.8 была ранее доказана другим способом):
Доказательство.
Фиксируем какое-либо число
![]() ,
например
,
например
![]() ,
и выберем
,
и выберем
![]() такое,
что при всех
такое,
что при всех
![]() ,
для которых
,
для которых
![]() ,
будет
,
будет
![]() .
Разобьём
.
Разобьём
![]() на
отрезки длины
на
отрезки длины
![]() :
:
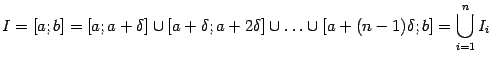
(мы положили
 ;
длина последнего отрезка может оказаться
меньше
;
длина последнего отрезка может оказаться
меньше
![]() ).
Выберем в качестве
).
Выберем в качестве
![]() середину
середину
![]() каждого
из отрезков:
каждого
из отрезков:
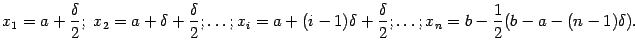
Тогда для каждого
![]() выполняется
неравенство
выполняется
неравенство
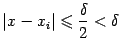 и,
следовательно,
и,
следовательно,
![]() .
Это неравенство эквивалентно такому:
.
Это неравенство эквивалентно такому:
![]() ,
или
,
или
![]() .
Поскольку точек
.
Поскольку точек
![]() конечное
число (а именно,
конечное
число (а именно,
![]() ),
то мы можем взять минимальное из чисел
),
то мы можем взять минимальное из чисел
![]() ,
,
![]() ,
и максимальное из чисел
,
и максимальное из чисел
![]() ,
,
![]() :
:
![]()
Тогда для любого
![]() верно
неравенство
верно
неравенство
![]() ,
и осталось взять
,
и осталось взять
![]() .
При этом для любого
.
При этом для любого
![]() будет
будет
![]() ,
что означает ограниченность функции
,
что означает ограниченность функции
![]() на
на
![]() .
.
Непрерывность обратной функции
Пусть
![]() --
функция, непрерывная на отрезке
--
функция, непрерывная на отрезке
![]() .
Предположим, что
.
Предположим, что
![]() монотонна
на
монотонна
на
![]() ;
пусть, для определённости, она монотонно
возрастает: из
;
пусть, для определённости, она монотонно
возрастает: из
![]() следует,
что
следует,
что
![]() .
Тогда образом отрезка
.
Тогда образом отрезка
![]() будет
отрезок
будет
отрезок
![]() ,
где
,
где
![]() и
и
![]() (действительно,
непрерывная функция принимает любое
промежуточное между
(действительно,
непрерывная функция принимает любое
промежуточное между
![]() и
и
![]() значение,
причём ровно один раз, что следует из
монотонности). Поэтому существует
обратная к
значение,
причём ровно один раз, что следует из
монотонности). Поэтому существует
обратная к
![]() функция
функция
![]() функция,
действующая из
функция,
действующая из
![]() в
в
![]() .
Очевидно, что
.
Очевидно, что
![]() монотонно
возрастает. (Если бы функция
монотонно
возрастает. (Если бы функция
![]() была
монотонно убывающей, то и обратная к
ней функция
была
монотонно убывающей, то и обратная к
ней функция
![]() тоже
была бы монотонно убывающей.)
тоже
была бы монотонно убывающей.)
Теорема
3.11Пусть
![]() --
непрерывная монотонная функция,
--
непрерывная монотонная функция,
![]() ,
,
![]() .
Тогда обратная к
.
Тогда обратная к
![]() функция
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() .
.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Доказательство.
Во-первых, заметим, что если
![]() ,
,
![]() ,
то
,
то
![]() .
.
Во-вторых, пусть
![]() ;
рассмотрим функцию
;
рассмотрим функцию
![]() ,
которая определена при
,
которая определена при
![]() .
Очевидно, что
.
Очевидно, что
![]() --
непрерывная на
--
непрерывная на
![]() функция,
поэтому она принимает наименьшее
значение
функция,
поэтому она принимает наименьшее
значение
![]() в
некоторой точке
в
некоторой точке
![]() :
:
![]()
Таким образом, если
![]() ,
то
,
то
![]() ,
то есть если
,
то есть если
![]() ,
то
,
то
![]() .
Последнее утверждение можно
переформулировать так: для любого числа
.
Последнее утверждение можно
переформулировать так: для любого числа
![]() найдётся
число
найдётся
число
![]() ,
такое что при
,
такое что при
![]() выполняется
неравенство
выполняется
неравенство
![]() .
(При этом
.
(При этом
![]() ,
,
![]() ,
,
![]() ,
,
![]() .)
Получили, что функция
.)
Получили, что функция
![]() удовлетворяет
определению равномерной непрерывности
на отрезке
удовлетворяет
определению равномерной непрерывности
на отрезке
![]() ;
тем самым доказано утверждение теоремы.
;
тем самым доказано утверждение теоремы.
Гиперболические функции и ареа-функции
Для рассмотрения дальнейших примеров нам понадобится определение гиперболических функций и ареа-функций, обратных к гиперболическим.
Определение 3.6Гиперболическим синусомназывается функция
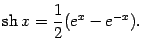
Гиперболическим косинусомназывается функция
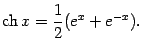
Гиперболическим тангенсомназывается функция

Гиперболическим котангенсомназывается функция
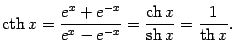
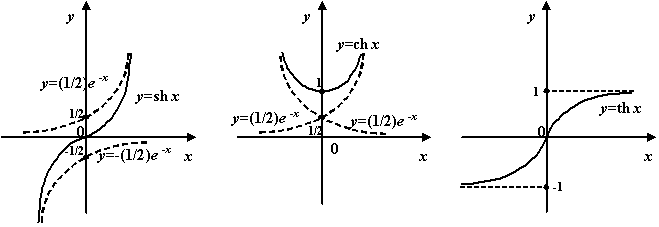
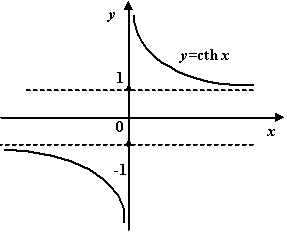
Рис.3.26.Графики гиперболических функций
Функции
![]() ,
,
![]() и
и
![]() --
нечётные; функция
--
нечётные; функция
![]() --
чётная. Области определения гиперболических
функций таковы:
--
чётная. Области определения гиперболических
функций таковы:
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
области значений-- следующие:
![]()
Упражнение 3.1Докажите сделанные утверждения о том, какой вид имеют области значений гиперболических функций.
Замечание 3.2В англоязычной литературе
используется обозначение
![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() .
.
Некоторые из свойств гиперболических функций схожи (но не всегда в точности совпадают) со свойствами соответствующих тригонометрических функций. Например, имеют место формулы:
|
|
|
|
|
|
|
|
|
|
|
|
и многие другие формулы, аналогичные известным формулам тригонометрии.
Упражнение 3.2Докажите приведённые выше формулы, исходя из определений гиперболических функций.
Подобно тому, как равенство
![]() выражает
тот факт, что точка координатной плоскости
выражает
тот факт, что точка координатной плоскости
![]() с
координатами
с
координатами
![]() ,
,
![]() при
изменении параметра
при
изменении параметра
![]() движется
по окружности радиуса 1, заданной
уравнением
движется
по окружности радиуса 1, заданной
уравнением
![]() (и
называемой тригонометрическим кругом),
равенство
(и
называемой тригонометрическим кругом),
равенство
![]() говорит
о том, что точка с координатами
говорит
о том, что точка с координатами
![]() ,
,
![]() движется
по равносторонней гиперболе, заданной
уравнением
движется
по равносторонней гиперболе, заданной
уравнением
![]() .
Отсюда и происходит название:
гиперболические функции.
.
Отсюда и происходит название:
гиперболические функции.
Функции
![]() ,
,
![]() непрерывны
и монотонно возрастают на своих областях
определения. Поэтому они имеют обратные
функции, которые также монотонно
возрастают и непрервыны. Функция,
обратная к функции
непрерывны
и монотонно возрастают на своих областях
определения. Поэтому они имеют обратные
функции, которые также монотонно
возрастают и непрервыны. Функция,
обратная к функции
![]() ,
называетсяобратным гиперболическим
синусом, илиареа-синусом, и
обозначается
,
называетсяобратным гиперболическим
синусом, илиареа-синусом, и
обозначается
![]() .
Имеем:
.
Имеем:
![]() ,
,
![]() .
Функция, обратная к функции
.
Функция, обратная к функции
![]() ,
называетсяобратным гиперболическим
тангенсом, илиареа-тангенсом, и
обозначается
,
называетсяобратным гиперболическим
тангенсом, илиареа-тангенсом, и
обозначается
![]() .
Итак,
.
Итак,
![]() ,
,
![]() .
.
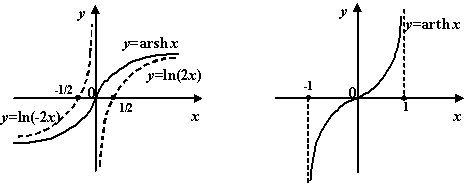
Рис.3.27.Графики
функций
![]() и
и
![]()
Функция
![]() ,
хотя и имеет разрыв в точке 0, монотонна
на интервалах
,
хотя и имеет разрыв в точке 0, монотонна
на интервалах
![]() и
и
![]() и
принимает каждое своё значение ровно
один раз. Поэтому существует обратная
функция, называемаяобратным
гиперболическим котангенсом, илиареа-котангенсом, обозначаемая
и
принимает каждое своё значение ровно
один раз. Поэтому существует обратная
функция, называемаяобратным
гиперболическим котангенсом, илиареа-котангенсом, обозначаемая
![]() .
Она определена на
.
Она определена на
![]() и
принимает значения в множестве
и
принимает значения в множестве
![]() .
.

Рис.3.28.График
функции
![]()
Функция
![]() не
является монотонной на всей своей
области определения. Однако монотонно
(и непрерывно) её ограничение на полуось
не
является монотонной на всей своей
области определения. Однако монотонно
(и непрерывно) её ограничение на полуось
![]() ,
при этом функция
,
при этом функция
![]() принимает
все значения из
принимает
все значения из
![]() .
Поэтому для этого ограничения существует
обратная функция, называемаяобратным
гиперболическим косинусом, илиареа-косинусоми обозначаемая
.
Поэтому для этого ограничения существует
обратная функция, называемаяобратным
гиперболическим косинусом, илиареа-косинусоми обозначаемая
![]() .
Она непрерывна на своей области
определения
.
Она непрерывна на своей области
определения
![]() и
принимает значения на
и
принимает значения на
![]() .
.
Возможен вариант: вместо ограничения
на
![]() можно
рассмотреть ограничение функции
можно
рассмотреть ограничение функции
![]() на
на
![]() ,
а затем функцию, обратную к этому
ограничению. Эту функцию часто также
называют ареа-косинусом и обозначают
,
а затем функцию, обратную к этому
ограничению. Эту функцию часто также
называют ареа-косинусом и обозначают
![]() ,
однако нужно чётко осознавать, что при
таком построении получается другая
функция (будем обозначать её здесь
,
однако нужно чётко осознавать, что при
таком построении получается другая
функция (будем обозначать её здесь
![]() ).
Итак,
).
Итак,
![]() и
и
![]() .
.

Рис.3.29.Графики
функций
![]() и
и
![]()
Замечание 3.3В англоязычной литературе
используется обозначение
![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() .
.
Упражнение 3.3Докажите, пользуясь определением гиперболических функций, что ареа-функции выражаются через логарифмическую функцию следующим образом:
![]()
![]()
![]()
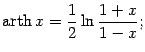
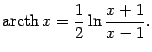
Примеры и упражнения
Пример 3.17Пусть функция
![]() определена
на интервале
определена
на интервале
![]() следующим
образом:
следующим
образом:
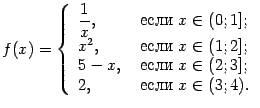
Найдём её область непрерывности и точки разрыва.
Поскольку внутри интервалов
![]() ,
,
![]() ,
,
![]() ,
,
![]() функция
функция
![]() совпадает
с ограничениями на эти интервалы
элементарных функций
совпадает
с ограничениями на эти интервалы
элементарных функций
![]() ,
,
![]() ,
,
![]() ,
2 соответственно, то все эти интервалы
входят в область непрерывности и точек
разрыва там нет. Точками разрыва могут
оказаться (но не обязательно окажутся!)
лишь точки на стыках этих интервалов,
то есть точки
,
2 соответственно, то все эти интервалы
входят в область непрерывности и точек
разрыва там нет. Точками разрыва могут
оказаться (но не обязательно окажутся!)
лишь точки на стыках этих интервалов,
то есть точки
![]() ,
,
![]() ,
,
![]() .
.
Для выяснения того, непрерывна ли функция
в точке
![]() ,
найдём пределы слева и справа:
,
найдём пределы слева и справа:
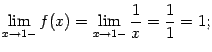
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
![]()
При этом мы воспользовались тем, что
как элементарная функция
![]() (с
областью определения
(с
областью определения
![]() ),
так и элементарная функция
),
так и элементарная функция
![]() (с
областью определения
(с
областью определения
![]() )
имеют
)
имеют
![]() внутренней
точкой своих областей определения,
непрерывны в этой точке, и значения
пределов можно найти прямой подстановкой.
Поскольку пределы слева и справа в
точке 1 совпали и, кроме того,
внутренней
точкой своих областей определения,
непрерывны в этой точке, и значения
пределов можно найти прямой подстановкой.
Поскольку пределы слева и справа в
точке 1 совпали и, кроме того,
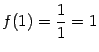 ,
то условия непрерывности в точке 1
выполнены; разрыва в этой точке нет.
,
то условия непрерывности в точке 1
выполнены; разрыва в этой точке нет.
Точно так же исследуем функцию на
непрерывность в точке
![]() .
Найдём пределы слева и справа:
.
Найдём пределы слева и справа:
![]()
![]()
Поскольку пределы слева и справа при
![]() существуют,
но не совпадают, функция имеет разрыв
первого рода при
существуют,
но не совпадают, функция имеет разрыв
первого рода при
![]() .
.
Теперь найдём пределы при
![]() и
и
![]() :
:
![]()
![]()
Здесь пределы слева и справа совпадают
между собой и со значением функции в
точке 3:
![]() .
Значит,
.
Значит,
![]() --
точка непрерывности.
--
точка непрерывности.
Итак, функция имеет единственную точку
разрыва
![]() ,
в которой происходит неустранимый
разрыв первого рода; область непрерывности
функции состоит из объединения двух
интервалов:
,
в которой происходит неустранимый
разрыв первого рода; область непрерывности
функции состоит из объединения двух
интервалов:
![]() .
.
Мгновенная скорость при прямолинейном движении
Пусть материальная точка движется по
координатной прямой
![]() ,
и её положение в момент времени
,
и её положение в момент времени
![]() имеет
координату
имеет
координату
![]() .Средняя скоростьточки за произвольный
промежуток времени
.Средняя скоростьточки за произвольный
промежуток времени
![]() ,
за который точка перемещается из
положения
,
за который точка перемещается из
положения
![]() в
положение
в
положение
![]() ,
определяется как
,
определяется как
 .
Если мы обозначим протекший промежуток
времени через
.
Если мы обозначим протекший промежуток
времени через
![]() ,
то
,
то
![]() и
и
![]() ,
поэтому
,
поэтому
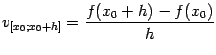 ,
при
,
при
![]() .
.
Мгновенная скоростьточки в момент
![]() определяется
как предел средней скорости за промежуток
времени от
определяется
как предел средней скорости за промежуток
времени от
![]() до
до
![]() (
(![]() ),
при условии
),
при условии
![]() .
Таким образом, получаем формулу, служащую
определением мгновенной скорости в
момент
.
Таким образом, получаем формулу, служащую
определением мгновенной скорости в
момент
![]() :
:
|
|
(4.1) |
Можно также рассматривать промежутки
времени, протекшие до момента
![]() ,
то есть промежутки от
,
то есть промежутки от
![]() до
до
![]() .
Тогда средняя скорость точки
.
Тогда средняя скорость точки
![]() за
этот промежуток времени будет равна
за
этот промежуток времени будет равна
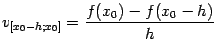 ,
при
,
при
![]() .
Если положить
.
Если положить
![]() ,
то, очевидно,
,
то, очевидно,
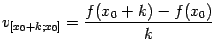 ,
при
,
при
![]() .
При этом придётся определять мгновенную
скорость в момент
.
При этом придётся определять мгновенную
скорость в момент
![]() формулой
формулой
|
|
(4.2) |
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Определение 4.1Число
![]() мы
будем называтьправой производной,
илипроизводной справа, функции
мы
будем называтьправой производной,
илипроизводной справа, функции
![]() в
точке
в
точке
![]() и
обозначать
и
обозначать
![]() или
или
![]() ,
а число
,
а число
![]() --левой производной, илипроизводной
слева, функции
--левой производной, илипроизводной
слева, функции
![]() в
точке
в
точке
![]() и
обозначать
и
обозначать
![]() или
или
![]() .
Иногда для уточнения говорят, что эти
производные вычислены по переменной
.
Иногда для уточнения говорят, что эти
производные вычислены по переменной
![]() .
.
Напомним ещё раз, что механический смысл
как левой, так и правой производной
координаты
![]() по
времени
по
времени
![]() --
это мгновенная скорость движения,
вычисленная в момент
--
это мгновенная скорость движения,
вычисленная в момент
![]() ,
но либо по интервалам времени,
предшествующим
,
но либо по интервалам времени,
предшествующим
![]() ,
либо по интервалам, последующим
,
либо по интервалам, последующим
![]() .
Эти две мгновенных скорости не обязаны,
вообще говоря, совпадать: если тело
покоилось до момента
.
Эти две мгновенных скорости не обязаны,
вообще говоря, совпадать: если тело
покоилось до момента
![]() ,
а затем двинулось с постоянной скоростью
,
а затем двинулось с постоянной скоростью
![]() ,
то мгновенная скорость, вычисленная по
предшествующим интервалам, очевидно,
равна
,
то мгновенная скорость, вычисленная по
предшествующим интервалам, очевидно,
равна
![]() (так
как до момента
(так
как до момента
![]() тело
покоилось), а мгновенная скорость,
вычисленная по последующим интервалам
времени, равна
тело
покоилось), а мгновенная скорость,
вычисленная по последующим интервалам
времени, равна
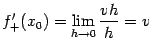 (
(![]() --
это изменение координаты
--
это изменение координаты
![]() точки,
движущейся со скоростью
точки,
движущейся со скоростью
![]() ,
за промежуток времени продолжительности
,
за промежуток времени продолжительности
![]() с
момента
с
момента
![]() до
момента
до
момента
![]() ).
Эти две мгновенных скорости различны
).
Эти две мгновенных скорости различны
Касательная к кривой на плоскости
Пусть на координатной плоскости
![]() построен
график функции
построен
график функции
![]() ,
и
,
и
![]() --
некоторая внутренняя точка области
определения
--
некоторая внутренняя точка области
определения
![]() .
Прямая, проходящая через точки
.
Прямая, проходящая через точки
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() (
(
![]() ), --
это секущая по отношению к графику
), --
это секущая по отношению к графику
![]() .
.
Касательнойк линии
![]() в
точке
в
точке
![]() называется
прямая
называется
прямая
![]() ,
служащая предельным положением секущих
(прямых
,
служащая предельным положением секущих
(прямых
![]() ),
при условии, что точка
),
при условии, что точка
![]() приближается,
следуя по линии
приближается,
следуя по линии
![]() ,
к точке касания
,
к точке касания
![]() .
.
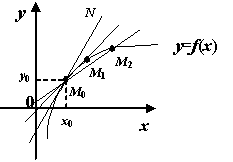
Рис.4.1.Касательная --
это предельное положение секущих![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Этому не вполне строгому определению
можно придать точный смысл, если задавать
положения всех прямых, проходящих через
точку
![]() ,
то есть секущих и касательной, их углом
наклона по отношению к положительному
направлению оси
,
то есть секущих и касательной, их углом
наклона по отношению к положительному
направлению оси
![]() .
Обозначим через
.
Обозначим через
![]() угол
наклона прямой
угол
наклона прямой
![]() .
Очевидно, что, вообще говоря, угол
.
Очевидно, что, вообще говоря, угол
![]() зависит
от выбора точки
зависит
от выбора точки
![]() :
:
![]() (считаем,
что точка
(считаем,
что точка
![]() фиксирована).
Так как секущая проходит через точки с
координатами
фиксирована).
Так как секущая проходит через точки с
координатами
![]() и
и
![]() ,
то
,
то

Если теперь обозначить через
![]() приращение
абсциссы
приращение
абсциссы
![]() при
переходе от точки
при
переходе от точки
![]() к
точке
к
точке
![]() ,
то есть
,
то есть
![]() ,
то получим, что
,
то получим, что
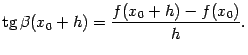
Приближение точки
![]() к
точке
к
точке
![]() вдоль
кривой
вдоль
кривой
![]() означает,
что
означает,
что
![]() ;
при этом угол
;
при этом угол
![]() приближается,
по определению, к углу
приближается,
по определению, к углу
![]() наклона
касательной
наклона
касательной
![]() :
:
![]()
Предположим, что этот предел существует
(что означает существование касательной)
и не равен
![]() .
Тогда, вследствие того, что тангенс
непрерывен при
.
Тогда, вследствие того, что тангенс
непрерывен при
![]() (
(
![]() ),
получаем, что
),
получаем, что
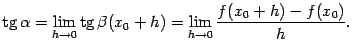
Итак, по определению, мы называем прямую
![]() наклонной
касательной(или просто касательной)
к линии
наклонной
касательной(или просто касательной)
к линии
![]() в
точке
в
точке
![]() ,
если она имеет тангенс угла
,
если она имеет тангенс угла
![]() наклона
к оси
наклона
к оси
![]() ,
равный
,
равный
|
|
(4.3) |
Число
![]() называютугловым коэффициентом касательнойк графику функции при
называютугловым коэффициентом касательнойк графику функции при
![]() .
.
Если же
![]() ,
то прямая
,
то прямая
![]() оказывается
вертикальной (перпендикулярной к оси
оказывается
вертикальной (перпендикулярной к оси
![]() ).
В этом случае будем говорить, что график
).
В этом случае будем говорить, что график
![]() имеетвертикальную касательнуюв точке
имеетвертикальную касательнуюв точке
![]() .
Этот случай соответствует тому, что
.
Этот случай соответствует тому, что
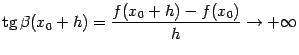
или
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
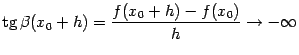
при
![]() .
.
Определение
4.2Число
![]() ,
в случае если задающий его предел
существует, называютпроизводнойфункции
,
в случае если задающий его предел
существует, называютпроизводнойфункции
![]() в
точке
в
точке
![]() и
обозначают
и
обозначают
![]() .
Иногда для уточнения говорят, что
производная вычислена по переменной
.
Иногда для уточнения говорят, что
производная вычислена по переменной
![]() .
.
Поскольку мы знаем, что уравнение прямой,
проходящей через точку
![]() с
угловым коэффициентом
с
угловым коэффициентом
![]() , --
это
, --
это
![]() (где
(где
![]() --
текущая точка прямой), то мы можем теперь
выписатьуравнение касательной к
графику
--
текущая точка прямой), то мы можем теперь
выписатьуравнение касательной к
графику
![]() при
при
![]() ,
то есть касательной, проходящей через
точку
,
то есть касательной, проходящей через
точку
![]() с
угловым коэффициентом, равным производной
с
угловым коэффициентом, равным производной
![]() функции
функции
![]() в
точке
в
точке
![]() :
:
![]()
Пусть дана некоторая кривая
![]() ,
и в точке
,
и в точке
![]() к
этой кривой проведена касательная.
Прямая, проходящая через точку касания
перпендикулярно касательной, называетсянормальюк линии
к
этой кривой проведена касательная.
Прямая, проходящая через точку касания
перпендикулярно касательной, называетсянормальюк линии
![]() .
.
Рис.4.2.Касательная
и нормаль к линии
![]()
Если касательная имеет угловой коэффициент
![]() ,
то нормаль имеет угловой коэффициент
,
то нормаль имеет угловой коэффициент
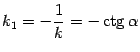 ,
поскольку ввиду перпендикулярности
нормали и касательной угол наклона
нормали равен
,
поскольку ввиду перпендикулярности
нормали и касательной угол наклона
нормали равен
![]() ,
а
,
а
![]() Поэтому
уравнение нормали к линии
Поэтому
уравнение нормали к линии
![]() ,
проведённой через точку
,
проведённой через точку
![]() ,
имеет вид:
,
имеет вид:
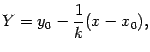
или

Производная
Итак, согласно предыдущим двум
определениям, производная
![]() функции
функции
![]() в
точке
в
точке
![]() ,правая производная
,правая производная
![]() илевая производная
илевая производная
![]() задаются,
соответственно, формулами
задаются,
соответственно, формулами
|
|
при этом в формуле
(4.3a)
функция должна быть определена на
некотором интервале
![]() ,
в формуле (4.3b) --
на некотором полуинтервале
,
в формуле (4.3b) --
на некотором полуинтервале
![]() ,
а в формуле (4.3c) --
на некотором полуинтервале
,
а в формуле (4.3c) --
на некотором полуинтервале
![]() .
.
Функция, имеющая
в точке
![]() производную
(соотв. левую производную, правую
производную), называетсядифференцируемой
(соотв. дифференцируемой
слева, дифференцируемой справа)
в точке
производную
(соотв. левую производную, правую
производную), называетсядифференцируемой
(соотв. дифференцируемой
слева, дифференцируемой справа)
в точке
![]() .
Функция, дифференцируемая во всех точках
некоторого интервала
.
Функция, дифференцируемая во всех точках
некоторого интервала![]() ,
называетсядифференцируемой
на интервале
,
называетсядифференцируемой
на интервале
![]() .
Пусть теперь
.
Пусть теперь![]() --
замкнутый отрезок. Функция, дифференцируемая
во всех точках интервала
--
замкнутый отрезок. Функция, дифференцируемая
во всех точках интервала![]() ,
дифференцируемая справа в точке
,
дифференцируемая справа в точке![]() и
дифференцируемая слева в точке
и
дифференцируемая слева в точке![]() ,
называетсядифференцируемой
на отрезке
,
называетсядифференцируемой
на отрезке
![]() .
.![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Вычислим производную
данной функции
![]() в
различных точках
в
различных точках![]() некоторого
интервала
некоторого
интервала![]() и
предположим, что производная
и
предположим, что производная![]() существует
при всех
существует
при всех![]() .
Тогда мы можем задать соответствие
между точками
.
Тогда мы можем задать соответствие
между точками![]() интервала
и числами
интервала
и числами![]() и
получаем функцию
и
получаем функцию![]() .
Эта функция
.
Эта функция![]() называетсяпроизводной
от функции
называетсяпроизводной
от функции
![]() (илипервой
производной
от
(илипервой
производной
от
![]() ).
).
С математической
точки зрения, разница между формулами
(4.3
a-c)
невелика: согласно теореме о связи
двустороннего предела с односторонними,
если существует производная
![]() ,
то существуют обе односторонние
производные (правая
,
то существуют обе односторонние
производные (правая![]() и
левая
и
левая![]() ),
и
),
и![]() .
Обратно, если существуют и равны друг
другу односторонние производные,
.
Обратно, если существуют и равны друг
другу односторонние производные,![]() ,
то существует и производная
,
то существует и производная![]() ,
совпадающая с их общим значением.
,
совпадающая с их общим значением.
В предположении,
что производная
![]() существует,
мы можем теперь сказать, что число
существует,
мы можем теперь сказать, что число![]() задаёт
мгновенную скорость изменения координаты
задаёт
мгновенную скорость изменения координаты![]() при
при![]() ;
с геометрической точки зрения, эта
скорость равна тангенсу угла наклона
касательной, проведённой к графику
;
с геометрической точки зрения, эта
скорость равна тангенсу угла наклона
касательной, проведённой к графику![]() при
при![]() :
чем быстрее растут (или убывают) значения
функции, тем круче наклонён график к
оси
:
чем быстрее растут (или убывают) значения
функции, тем круче наклонён график к
оси![]() (составляя,
соответственно, положительный или
отрицательный угол с осью
(составляя,
соответственно, положительный или
отрицательный угол с осью![]() ).
).

Рис.4.3.Скорость роста значений функции соответствует величине тангенса угла наклона касательной
Замечание
4.1 В
числителе дроби, предельное значение
которой даёт производную, стоит выражение
![]() .
Оно называется приращением функции. В
знаменателе стоит величина
.
Оно называется приращением функции. В
знаменателе стоит величина![]() .
Она называется приращением аргумента.
Величина
.
Она называется приращением аргумента.
Величина![]() называется
разностным отношением Условие
называется
разностным отношением Условие![]() можно,
очевидно, записать в виде
можно,
очевидно, записать в виде![]() (кстати,
база
(кстати,
база![]() эквивалентна
базе
эквивалентна
базе![]() ).
Тем самым определение производной можно
записать в таком виде:
).
Тем самым определение производной можно
записать в таком виде:
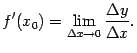
От такой записи
происходит обозначение производной в
виде
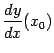 .
.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример
4.1
Рассмотрим линейную функцию
![]() .
Тогда
.
Тогда![]() ,
,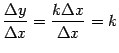 и
и![]() при
любом
при
любом![]() .
Получаем, что для линейной функции
производная в любой точке равна угловому
коэффициенту
.
Получаем, что для линейной функции
производная в любой точке равна угловому
коэффициенту![]() .
(Что неудивительно: ведь касательная к
прямой, служащей графиком линейной
функции, -- это та же самая прямая, а
угловой коэффициент касательной равен
производной!) В частности, при
.
(Что неудивительно: ведь касательная к
прямой, служащей графиком линейной
функции, -- это та же самая прямая, а
угловой коэффициент касательной равен
производной!) В частности, при![]() получаем,
что производная любой постоянной, то
есть функции
получаем,
что производная любой постоянной, то
есть функции![]() ,
равна 0:
,
равна 0:
|
|
(4.5) |
а при
![]() и
и![]() получаем,
что
получаем,
что
|
|
(4.6) |
Пример
4.2 Пусть
![]() и
и![]() .
Вычислим односторонние производные
.
Вычислим односторонние производные![]() и
и![]() .
.
При
![]() имеем
имеем![]() и
и![]() .
Значит, разностное отношение равно
.
Значит, разностное отношение равно и
и![]()
При
![]() имеем
имеем![]() и
и![]() .
Значит, разностное отношение равно
.
Значит, разностное отношение равно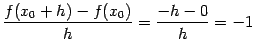 и
и![]()
Графически это означает следующее. Мы строим касательную к графику
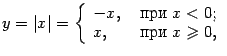
в точке
![]() ,
сначала пользуясь секущими
,
сначала пользуясь секущими![]() с
точкой
с
точкой![]() правее
правее![]() .
Эта касательная, как и все такие секущие,
совпадают между собой и имеют уравнение
.
Эта касательная, как и все такие секущие,
совпадают между собой и имеют уравнение![]() ,
задающее прямую, наклонённую под углом
,
задающее прямую, наклонённую под углом![]() к
оси
к
оси![]() (
(![]() ).
Далее, мы строим касательную, пользуясь
секущими
).
Далее, мы строим касательную, пользуясь
секущими![]() с
точкой
с
точкой![]() левее
левее![]() .
Все такие секущие и касательная, по ним
построенная, совпадают между собой и
имеют уравнение
.
Все такие секущие и касательная, по ним
построенная, совпадают между собой и
имеют уравнение![]() ,
задающее прямую, наклонённую под углом
,
задающее прямую, наклонённую под углом![]() к
оси
к
оси![]() (
(![]() ).
).
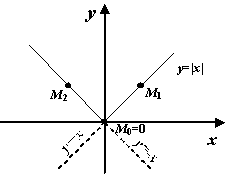
Рис.4.4.График
![]() имеет
излом при
имеет
излом при
![]()
Таким образом,
неравенство левой и правой производной
выражает тот геометрический факт, что
линия
![]() имеет
при
имеет
при![]() излом
под углом
излом
под углом![]() и
не имеет общей касательной сразу к двум
сторонам этого угла.
и
не имеет общей касательной сразу к двум
сторонам этого угла.
Покажем теперь, что дифференцируемая функция не может быть разрывной.
Теорема
4.1 Пусть
функция
![]() дифференцируема
(дифференцируема слева, дифференцируема
справа) в точке
дифференцируема
(дифференцируема слева, дифференцируема
справа) в точке![]() .
Тогда
.
Тогда![]() непрерывна
(соотв. непрерывна слева, непрерывна
справа) в этой точке
непрерывна
(соотв. непрерывна слева, непрерывна
справа) в этой точке![]() .
.
Доказательство. Из существования производной
следует, что
откуда
![]()
что и означает
непрерывность функции
![]() в
точке
в
точке![]() .
.
Для доказательства
теоремы в случае существования
односторонних производных достаточно
сменить базу
![]() на
базу
на
базу![]() или
или![]() .
.
Замечание
4.2
Предыдущий пример показывает, что
обратное утверждение неверно: функция
не обязательно имеет производную во
всех тех точках, где она непрерывна.
Действительно, функция
![]() непрерывна
при
непрерывна
при![]() ,
но не имеет производной в точке 0.
,
но не имеет производной в точке 0.
Более того, можно построить пример такой функции, которая непрерывна во всех точках числовой прямой, но не имеет производной ни в одной из этих точек.
Замечание
4.3 Заметим,
что доказанная теорема гарантирует
непрерывность функции, имеющей производную
в точке
![]() ,
только в этой самой точке
,
только в этой самой точке![]() ,
но не на некотором интервале, окружающем
,
но не на некотором интервале, окружающем![]() .
Примером функции, имеющей производную
при
.
Примером функции, имеющей производную
при![]() ,
но разрывной при всех
,
но разрывной при всех![]() ,
служит функция
,
служит функция
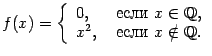
(Напомним, что
через
![]() обозначается
множество всех рациональных чисел.
Рациональные числа, как и иррациональные,
плотно расположены на числовой оси
обозначается
множество всех рациональных чисел.
Рациональные числа, как и иррациональные,
плотно расположены на числовой оси![]() :
между любыми двумя рациональными числами
найдётся иррациональное число, а между
двумя иррациональными -- рациональное.)
Действительно,
:
между любыми двумя рациональными числами
найдётся иррациональное число, а между
двумя иррациональными -- рациональное.)
Действительно,![]() ;
если
;
если![]() --
рациональное число, то разностное
отношение
--
рациональное число, то разностное
отношение ,
а если
,
а если![]() --
иррациональное, то
--
иррациональное, то .
И в том, и в другом случае разностное
отношение стремится к 0 при
.
И в том, и в другом случае разностное
отношение стремится к 0 при![]() ,
так что существует производная
,
так что существует производная![]() .
Однако, как нетрудно заметить, функция
.
Однако, как нетрудно заметить, функция![]() разрывна
во всех точках
разрывна
во всех точках![]() ,
кроме
,
кроме![]() .
.
Замечание
4.4 Заметим
также, что даже если функция имеет
производную на некотором интервале,
окружающем точку
![]() ,
значение
,
значение![]() может
оказаться не равным пределу значений
может
оказаться не равным пределу значений![]() при
при![]() ,
то есть производная
,
то есть производная![]() может
оказаться разрывной функцией. Примером
такой функции с всюду существующей, но
разрывной производной
может
оказаться разрывной функцией. Примером
такой функции с всюду существующей, но
разрывной производной![]() может
служить функция
может
служить функция
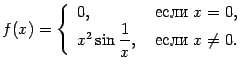
Производная этой функции, как мы покажем ниже, равна
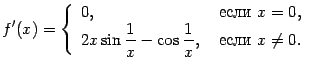
Нетрудно видеть,
что эта функция имеет разрыв второго
рода в точке 0, из-за слагаемого
![]() ,
совершающего бесконечное число колебаний
амплитуды 1 в любой, как угодно малой,
окрестности точки 0
,
совершающего бесконечное число колебаний
амплитуды 1 в любой, как угодно малой,
окрестности точки 0
Свойства производных
Покажем, что множество функций, имеющих
производную в некоторой фиксированной
точке
![]() ,
замкнуто относительно арифметических
операций с этими функциями. А именно,
докажем следующую теорему, дающую
основные правила дифференцирования.
,
замкнуто относительно арифметических
операций с этими функциями. А именно,
докажем следующую теорему, дающую
основные правила дифференцирования.
Теорема 4.2Пусть функции
![]() и
и
![]() имеют
производные в точке
имеют
производные в точке
![]() .
Тогда функции
.
Тогда функции
![]() ,
,
![]() ,
,
![]() ,
а в случае
,
а в случае
![]() также
также
 имеют
производные в точке
имеют
производные в точке
![]() ,
которые выражаются следующими формулами:
,
которые выражаются следующими формулами:
|
|
(4.7) |
|
|
(4.8) |
|
|
(4.9) |
|
|
(4.10) |
Аналогичные утверждения и формулы
имеют место также для односторонних
производных
![]() (
(![]() ).
).
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Доказательство.
Докажем формулу (4.7). Пусть аргументу
![]() дано
приращение
дано
приращение
![]() ;
при этом функция
;
при этом функция
![]() получает
приращение
получает
приращение
![]() ,
а функция
,
а функция
![]() --
приращение
--
приращение
![]() .
Их сумма
.
Их сумма
![]() получит
тогда приращение
получит
тогда приращение
![]()
Значит,
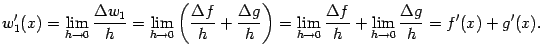
Совершенно аналогично доказывается формула (4.8).
Докажем теперь формулу (4.9). Пусть снова
![]() и
и
![]() --
приращения функций, соответствующие
приращению
--
приращения функций, соответствующие
приращению
![]() аргумента
аргумента
![]() .
Тогда
.
Тогда
![]() ,
,
![]() и
приращением произведения будет
и
приращением произведения будет
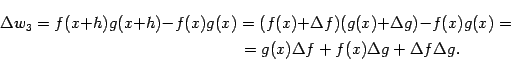
Поэтому, по свойствам пределов,
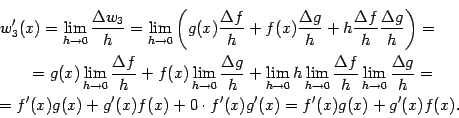
При этом мы вынесли множители
![]() и
и
![]() за
знак предела
за
знак предела
![]() как
постоянные, не зависящие от переменного
как
постоянные, не зависящие от переменного
![]() ,
к которому относится база предела.
,
к которому относится база предела.
Докажем теперь формулу (4.10). Заметим, что
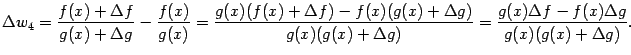
Поэтому, согласно правилам вычисления пределов,
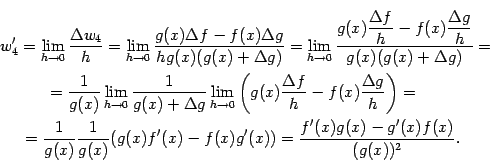
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
При этом мы вынесли за знак предела
постоянный (то есть не зависящий от
![]() )
множитель
)
множитель
![]() и
воспользовались тем, что
и
воспользовались тем, что
![]() при
при
![]() ,
что означает непрерывность функции
,
что означает непрерывность функции
![]() в
точке
в
точке
![]() .
Но ранее мы доказали, что всякая
дифференцируемая в точке
.
Но ранее мы доказали, что всякая
дифференцируемая в точке
![]() функция
непрерывна в точке
функция
непрерывна в точке
![]() (
теорема 4.1).
(
теорема 4.1).
Замечание
4.5Обозначим функцию
![]() через
через
![]() ,
а функцию
,
а функцию
![]() через
через
![]() .
Тогда формулы (4.7 - 4.10) можно более
коротко записать в виде
.
Тогда формулы (4.7 - 4.10) можно более
коротко записать в виде
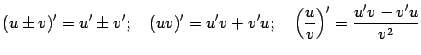 (при
(при![]()
Именно в таком кратком виде мы и рекомендуем запоминать эти формулы.
Следствие
4.1Применяя формулу (4.9) к случаю,
когда
![]() ,
и учитывая, что
,
и учитывая, что
![]() (см. формулу
(4.5)), мы получаем, что
(см. формулу
(4.5)), мы получаем, что
![]()
то есть что постоянный множитель можно выносить из под знака производной.
Из этого следствия и формулы (4.7) получается
следующее свойство производных: если
![]() и
и
![]() --
постоянные и
--
постоянные и
![]() --
дифференцируемые в точке
--
дифференцируемые в точке
![]() функции,
то
функции,
то
|
|
(4.11) |
Если операцию вычисления производной
в точке
![]() обозначить
обозначить
![]() ,
то есть
,
то есть
![]() ,
то равенство (4.11) означаетлинейностьэтой операции дифференцирования в
точке:
,
то равенство (4.11) означаетлинейностьэтой операции дифференцирования в
точке:
![]()
Поскольку дифференцируемость функции
на интервале или отрезке мы определяли
как дифференцируемость в каждой точке
этого интервала или отрезка, то тем
самым мы показали, что операция
![]() перехода
от функции
перехода
от функции
![]() к
её производной
к
её производной
![]() ,
,
![]() ,
также обладает свойством линейности:
,
также обладает свойством линейности:
![]()
При этом в случае отрезка действие
![]() на
функцию в точке, являющейся одним из
концов отрезка, понимается как вычисление
соответствующей односторонней
производной: в левом конце -- правой,
а в правом конце -- левой.
на
функцию в точке, являющейся одним из
концов отрезка, понимается как вычисление
соответствующей односторонней
производной: в левом конце -- правой,
а в правом конце -- левой.
Эти результаты можно выразить ещё и
таким образом. Рассмотрим пространство
![]() всех
функций
всех
функций
![]() ,
определённых на некотором фиксированном
интервале
,
определённых на некотором фиксированном
интервале
![]() и
имеющих производную
и
имеющих производную
![]() в
точке
в
точке
![]() .
Тогда операции умножения на постоянные
множители и сложения не выводят из этого
пространства, то есть пространство
.
Тогда операции умножения на постоянные
множители и сложения не выводят из этого
пространства, то есть пространство
![]() --
этолинейное пространство; при этом
операция
--
этолинейное пространство; при этом
операция
![]() --
этолинейная операцияиз пространства
--
этолинейная операцияиз пространства
![]() в
линейное пространство вещественных
чисел:
в
линейное пространство вещественных
чисел:
![]()
То же верно и для пространств функций,
дифференцируемых на интервале
![]() (обозначим
это пространство
(обозначим
это пространство
![]() )
или на отрезке
)
или на отрезке
![]() (обозначим
это пространство
(обозначим
это пространство
![]() ).
Оба этих пространства -- линейные (то
есть замкнуты относительно применения
к функциям из этих пространств операций
сложения и умножения на постоянные), а
операция дифференцирования
).
Оба этих пространства -- линейные (то
есть замкнуты относительно применения
к функциям из этих пространств операций
сложения и умножения на постоянные), а
операция дифференцирования
![]() действует
как линейная операция из этих линейных
пространств в линейное пространство
функций, непрерывных на данном интервале
(обозначим это пространство
действует
как линейная операция из этих линейных
пространств в линейное пространство
функций, непрерывных на данном интервале
(обозначим это пространство
![]() ;
см. предложение 3.4) или отрезке (обозначим
это пространство
;
см. предложение 3.4) или отрезке (обозначим
это пространство
![]() ;
также см. предложение 3.4), так как в
соответствии с теоремой 4.1 производная
каждой дифференцируемой функции
;
также см. предложение 3.4), так как в
соответствии с теоремой 4.1 производная
каждой дифференцируемой функции
![]() --
это непрерывная функция
--
это непрерывная функция
![]() :
:
![]()
![]()
Тем самым операция
![]() --
это линейная функция, областью определения
которой служит пространство всех
дифференцируемых функций, а область
значений
--
это линейная функция, областью определения
которой служит пространство всех
дифференцируемых функций, а область
значений
![]() лежит
в пространстве непрерывных функций.
Функции, областями определения и
областями значения которых служат
некоторые пространства функций, в
математике принято называтьоператорами.
Таким образом, операция дифференцирования
лежит
в пространстве непрерывных функций.
Функции, областями определения и
областями значения которых служат
некоторые пространства функций, в
математике принято называтьоператорами.
Таким образом, операция дифференцирования
![]() --
этолинейный операториз линейного
пространства
--
этолинейный операториз линейного
пространства
![]() в
линейное пространство
в
линейное пространство
![]() и
из линейного пространства
и
из линейного пространства
![]() в
линейное пространство
в
линейное пространство
![]() .
.
Производные некоторых элементарных функций
1. Выше мы уже рассмотрели линейную
функцию
![]() и
показали, что её производная равна
угловому коэффициенту
и
показали, что её производная равна
угловому коэффициенту
![]() :
:
![]()
2. Рассмотрим функцию
![]() .
Дадим аргументу
.
Дадим аргументу
![]() приращение
приращение
![]() и
найдём приращение функции:
и
найдём приращение функции:
![]() .
Поэтому
.
Поэтому
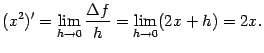
(Можно доказать эту формулу и так:
![]()
Здесь мы применили формулу (4.9).) Точно
так же для функции
![]() получаем:
получаем:
![]() ,
откуда
,
откуда
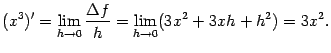
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
(И здесь, применяя формулу (4.9), мы можем действовать так:
![]()
Такие же вычисления для функции
![]() при
целом
при
целом
![]() можно
провести, разложив
можно
провести, разложив
![]() по
формуле бинома Ньютона (см. гл. 2).
При этом получится формула
по
формуле бинома Ньютона (см. гл. 2).
При этом получится формула
|
|
(4.12) |
(Проведите это вычисление самостоятельно
в качестве упражнения. Другой способ
доказательства этой формулы --
представить
![]() в
виде
в
виде
![]() и
применить метод математической индукции,
воспользовавшись тем, что при
и
применить метод математической индукции,
воспользовавшись тем, что при
![]() и
3 формула уже доказана.) При
и
3 формула уже доказана.) При
![]() и
и
![]() формула
(4.12) совпадает, соответственно, с формулами
(4.5) и (4.6). Ниже мы докажем, что эта формула
верна при любом
формула
(4.12) совпадает, соответственно, с формулами
(4.5) и (4.6). Ниже мы докажем, что эта формула
верна при любом
![]() ,
в том числе при дробных и отрицательных
значениях
,
в том числе при дробных и отрицательных
значениях
![]() .
.
3. Найдём производную функции
![]() в
точке
в
точке
![]() .
Преобразуем приращение функции следующим
образом:
.
Преобразуем приращение функции следующим
образом:
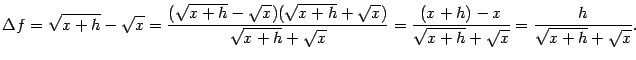
Поэтому
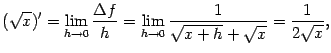
поскольку
![]() вследствие
непрерывности элементарной функции
вследствие
непрерывности элементарной функции
![]() в
любой точке
в
любой точке
![]() .
Получили в итоге формулу
.
Получили в итоге формулу
![]() ,
то есть формулу (4.12) при
,
то есть формулу (4.12) при
![]() .
.
4. Пусть
 ,
где
,
где
![]() .
Производную этой функции можно подсчитать
по формуле производной частного (формула
(4.10)):
.
Производную этой функции можно подсчитать
по формуле производной частного (формула
(4.10)):
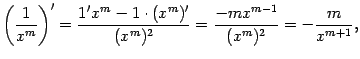
то есть
![]() .
Эта формула совпадает с формулой (4.12)
при отрицательных целых
.
Эта формула совпадает с формулой (4.12)
при отрицательных целых
![]() .
.
В частности, получаем при
![]()
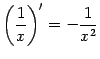
и при
![]()

5. Пусть
![]() .
Тогда приращение функции равно
.
Тогда приращение функции равно
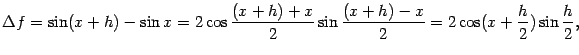
а производная --
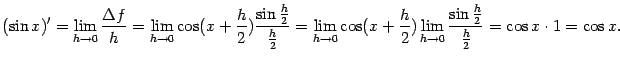
При этом мы воспользовались тем, что
![]() ,
так как
,
так как
![]() --
непрерывная функция, и тем, что
--
непрерывная функция, и тем, что
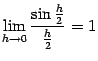 (это
первый замечательный предел).
(это
первый замечательный предел).
6. Пусть
![]() .
Тогда приращение функции равно
.
Тогда приращение функции равно

а производная --
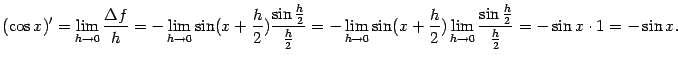
При этом мы воспользовались непрерывностью
синуса, откуда
![]() и
первым замечательным пределом.
и
первым замечательным пределом.
7. Рассмотрим функцию
![]() как
отношение
как
отношение
![]() и
применим для нахождения производной
формулу (4.10).
Получаем:
и
применим для нахождения производной
формулу (4.10).
Получаем:
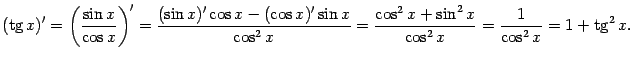
8. Аналогично, для функции
![]() получаем
получаем
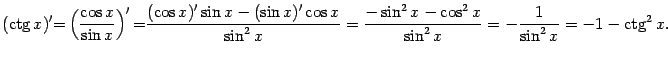
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
9. Пусть
![]() (
(
![]() ).
Тогда приращение функции равно
).
Тогда приращение функции равно
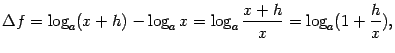
а разностное отношение --
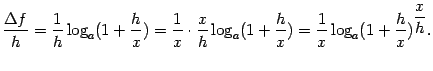
Теперь вычислим производную:
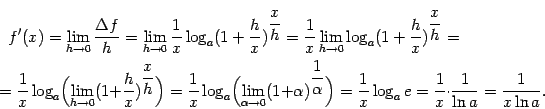
При вычислении предела мы, во-первых,
воспользовались непрерывностью
логарифмической функции и переставили
знаки предела и логарифма; во-вторых,
сделали замену
![]() ,
при этом
,
при этом
![]() при
при
![]() ;
в-третьих, был использован второй
замечательный предел:
;
в-третьих, был использован второй
замечательный предел:
![]() .
.
Из полученной формулы

при
![]() вытекает,
что
вытекает,
что
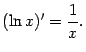
Пример 4.3Найдём производную функции
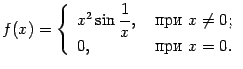
При
![]() вычислим
производную как производную произведения:
вычислим
производную как производную произведения:
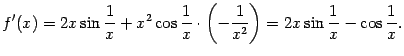
При
![]() производную
вычислим по формуле, служащей определением
производной:
производную
вычислим по формуле, служащей определением
производной:
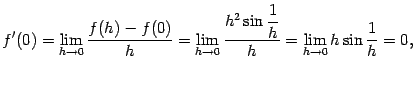
поскольку получили предел произведения
бесконечно малой величины
![]() и
ограниченной величины
и
ограниченной величины
![]() .
Итак,
.
Итак,
![]() ,
однако это значение не является пределом
,
однако это значение не является пределом
![]() при
при
![]() ,
то есть производная
,
то есть производная
![]() имеет
при
имеет
при
![]() разрыв
второго рода. Действительно, в выражении
для
разрыв
второго рода. Действительно, в выражении
для
![]() при
при
![]() первое
слагаемое
первое
слагаемое
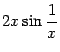 стремится
к 0 при
стремится
к 0 при
![]() ,
однако второе слагаемое
,
однако второе слагаемое
 не
стремится ни к какому пределу при
не
стремится ни к какому пределу при
![]() ,
совершая вблизи 0 бесконечно много
колебаний.
,
совершая вблизи 0 бесконечно много
колебаний.
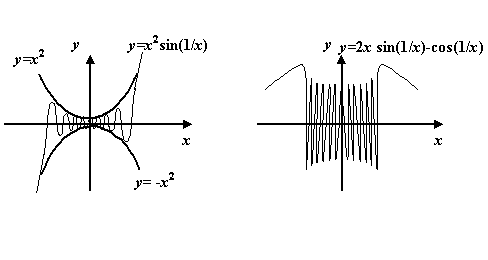
Рис.4.5.Графики
функции
![]() и
её производной
и
её производной
![]()
Этот пример показывает, что производная, даже если она всюду существует, не обязана быть непрерывной функцией.
Дифференциал
Определение
4.3Пусть дана функция
![]() ,
и
,
и
![]() --
внутренняя точка её области определения.
Придадим аргументу приращение
--
внутренняя точка её области определения.
Придадим аргументу приращение
![]() и
рассмотрим приращение функции
и
рассмотрим приращение функции
![]()
Если это приращение
![]() можно
представить в виде
можно
представить в виде
![]()
где величина
![]() не
зависит от приращения
не
зависит от приращения
![]() ,
а
,
а
![]() --
бесконечно малая при базе
--
бесконечно малая при базе
![]() величина,
имеющая больший порядок малости, чем
величина,
имеющая больший порядок малости, чем
![]() ,
то произведение
,
то произведение
![]() называетсядифференциалом функции
называетсядифференциалом функции
![]() в
точке
в
точке
![]() и
обозначается
и
обозначается
![]() или
просто
или
просто
![]() .
.
Таким образом, дифференциал
![]() --
это функция двух аргументов
--
это функция двух аргументов
![]() и
и
![]() ,
причём от переменного приращения
,
причём от переменного приращения
![]() дифференциал
зависит линейно (
дифференциал
зависит линейно (![]() входит в выражение, задающее
входит в выражение, задающее
![]() ,
как множитель, стоящий в первой степени).
Заметим, что в формуле
,
как множитель, стоящий в первой степени).
Заметим, что в формуле
![]()
второе слагаемое в правой части имеет
порядок малости, больший, чем у
![]() ,
и, следовательно, при
,
и, следовательно, при
![]() больший,
чем у
больший,
чем у
![]() .
Поэтомудифференциал
.
Поэтомудифференциал
![]() --
это главная, линейная по
--
это главная, линейная по
![]() ,
часть приращения функции.
,
часть приращения функции.
Теорема 4.3Функция
![]() имеет
дифференциал
имеет
дифференциал
![]() в
точке
в
точке
![]() тогда
и только тогда, когда она имеет производную
тогда
и только тогда, когда она имеет производную
![]() в
этой точке; при этом
в
этой точке; при этом
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Доказательство.
Пусть функция
![]() имеет
дифференциал, то есть её приращение
можно представить в виде
имеет
дифференциал, то есть её приращение
можно представить в виде
![]() .
Разделим обе части равенства на
.
Разделим обе части равенства на
![]() :
:

При
![]() в
правой части предел первого слагаемого
равен
в
правой части предел первого слагаемого
равен
![]() ,
поскольку эта величина не зависит от
,
поскольку эта величина не зависит от
![]() и,
следовательно, при вычислении предела
считается постоянной. Далее,
и,
следовательно, при вычислении предела
считается постоянной. Далее,
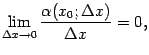
так как, по определению дифференциала,
![]() имеет
более высокий порядок малости, нежели
имеет
более высокий порядок малости, нежели
![]() .
Значит, существует предел
.
Значит, существует предел
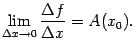
Но этот предел, по определению, равен
производной
![]() .
Значит, функция имеет производную в
точке
.
Значит, функция имеет производную в
точке
![]() ,
и
,
и
![]() ,
откуда
,
откуда
![]()
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пусть теперь функция
![]() имеет
производную
имеет
производную
![]() .
Это означает, что
.
Это означает, что
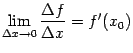 .
По теореме о связи пределов и бесконечно
малых, это эквивалентно тому, что величина
.
По теореме о связи пределов и бесконечно
малых, это эквивалентно тому, что величина
 является
бесконечно малой. Умножим обе части
последнего равенства на
является
бесконечно малой. Умножим обе части
последнего равенства на
![]() и
получим:
и
получим:
![]()
Получили представление приращения
функции в виде
![]() ,
где
,
где
![]() ,
а величина
,
а величина
![]() ,
очевидно, имеет больший порядок малости,
чем
,
очевидно, имеет больший порядок малости,
чем
![]() ,
поскольку
,
поскольку
![]() при
при
![]() .
Тем самым, функция
.
Тем самым, функция
![]() имеет
в точке
имеет
в точке
![]() дифференциал,
который имеет вид
дифференциал,
который имеет вид
![]() .
.
Геометрический смысл дифференциала
![]() мы
выясним, исходя из найденного ранее
геометрического смысла производной.
Поскольку производная
мы
выясним, исходя из найденного ранее
геометрического смысла производной.
Поскольку производная
![]() --
это угловой коэффициент
--
это угловой коэффициент
![]() касательной
к графику функции при
касательной
к графику функции при
![]() ,
то дифференциал
,
то дифференциал
![]() --
это приращение ординаты
--
это приращение ординаты
![]() точки
касательной
точки
касательной
![]()
к графику функции
![]() ,
когда абсцисса точки касательной
получает приращение
,
когда абсцисса точки касательной
получает приращение
![]() :
:
![]()
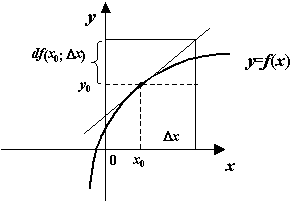
Рис.4.6.Дифференциал равен приращению ординаты касательной
Замечание
4.6Заметим, что для функции
![]() производная
равна 1, так что дифференциал
производная
равна 1, так что дифференциал
![]() равен
равен
![]() ,
то есть
,
то есть
![]() .
Поэтому можно всюду вместо приращения
независимой переменной
.
Поэтому можно всюду вместо приращения
независимой переменной
![]() писать
её дифференциал
писать
её дифференциал
![]() .
При этом получается, что для произвольной
дифференцируемой функции
.
При этом получается, что для произвольной
дифференцируемой функции
![]()
![]()
Замечание
4.7Часто в обозначении дифференциала
функции пропускают второй аргумент
![]() ,
от которого
,
от которого
![]() зависит
линейно, и пишут короче:
зависит
линейно, и пишут короче:
![]()
Однако нужно чётко понимать, что это
лищь сокращённая запись, и на самом деле
дифференциал -- это функция двух
аргументов
![]() и
и
![]() ,
линейная по
,
линейная по
![]() .
.
Замечание
4.8Поскольку для функции
![]() дифференциал
записывается как
дифференциал
записывается как
![]() ,
то, деля на
,
то, деля на
![]() ,
получаем
,
получаем
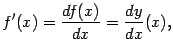
что придаёт смысл обозначению производной
в виде отношения дифференциалов. Это
обозначение было введено нами ранее,
однако выше мы не придавали дроби
![]() смысла
некоторого отношения двух величин, а
смогли сделать это только сейчас.
смысла
некоторого отношения двух величин, а
смогли сделать это только сейчас.
Производная композиции
Пусть
![]() и
и
![]() --
такие числовые функции, что определена
их композиция
--
такие числовые функции, что определена
их композиция
![]() .
Предположим, что функция
.
Предположим, что функция
![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки
![]() ,
а функция
,
а функция
![]() --
в некоторой окрестности точки
--
в некоторой окрестности точки
![]() .
Тогда имеет место следующее утверждение.
.
Тогда имеет место следующее утверждение.
Теорема 4.4Если функция
![]() имеет
производную
имеет
производную
![]() ,
а функция
,
а функция
![]() --
производную
--
производную
![]() ,
то композиция
,
то композиция
![]() имеет
производную
имеет
производную
|
|
(4.13) |
Доказательство.
Рассмотрим приращение функции
![]() ,
соответствующее приращению
,
соответствующее приращению
![]() переменного
переменного
![]() :
:
![]()
где
![]() и
и
![]() .
Так как функция
.
Так как функция
![]() имеет
дифференциал в точке
имеет
дифференциал в точке
![]() (см.
теорему 4.3), то
(см.
теорему 4.3), то
![]()
где
![]() при
при
![]() и
и
![]() при
при
![]() .
Раскрываем скобки далее:
.
Раскрываем скобки далее:
|
|
|
|
|
|
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Теперь, в соответствии с теоремой 4.3,
осталось доказать, что в последней
формуле в квадратных скобках стоит
величина, бесконечно малая при
![]() .
Первое слагаемое
.
Первое слагаемое
![]() бесконечно
мало, поскольку
бесконечно
мало, поскольку
![]() вообще
не зависит от
вообще
не зависит от
![]() ,
а
,
а
![]() --
бесконечно малая при базе
--
бесконечно малая при базе
![]() .
Во втором слагаемом
.
Во втором слагаемом
![]() постоянной
является величина
постоянной
является величина
![]() .
Покажем, что
.
Покажем, что
![]() при
при
![]() .
Так как функция
.
Так как функция
![]() имеет
производную при
имеет
производную при
![]() ,
то
,
то
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
откуда
,
откуда
![]() и,
следовательно,
и,
следовательно,
![]() при
при
![]() .
Поэтому
.
Поэтому
![]() при
при
![]() ,
по предположению о величине
,
по предположению о величине
![]() .
Для третьего слагаемого
.
Для третьего слагаемого
![]() заметим,
что
заметим,
что
![]() ,
как только что было доказано, есть
бесконечно малая и, следовательно,
локально ограниченная функция при
,
как только что было доказано, есть
бесконечно малая и, следовательно,
локально ограниченная функция при
![]() ,
а
,
а
![]() --
бесконечно малая. Значит, их произведение
также бесконечно мало при
--
бесконечно малая. Значит, их произведение
также бесконечно мало при
![]() .
Тем самым, в квадратных скобках стоит
сумма трёх бесконечно малых, которая
также является бесконечно малой
величиной. Теорема доказана.
.
Тем самым, в квадратных скобках стоит
сумма трёх бесконечно малых, которая
также является бесконечно малой
величиной. Теорема доказана.
Замечание
4.9Мы можем пояснить происхождение
формулы (4.13), то есть формулы
![]() ,
где
,
где
![]() ,
записав её в виде
,
записав её в виде

Эта формула получается предельным переходом из очевидного равенства
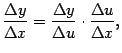
однако такое доказательство формулы
(4.13) имеет существенный недостаток,
поскольку ниоткуда не следует, что
![]() при
всех
при
всех
![]() .
Тем не менее, смысл формулы для производной
композиции функций при этом, несомненно,
проясняется.
.
Тем не менее, смысл формулы для производной
композиции функций при этом, несомненно,
проясняется.
Пример 4.4Пусть
![]() ,
то есть
,
то есть
![]() ,
где
,
где
![]() :
данная функция представлена в виде
композиции функций
:
данная функция представлена в виде
композиции функций
![]() и
и
![]() .
Тогда для нахождения производной мы
можем применить формуду производной
композиции. Поскольку
.
Тогда для нахождения производной мы
можем применить формуду производной
композиции. Поскольку
![]() и
и
![]() (нижний
индекс мы пишем для напоминания о том,
по какой переменной берётся производная),
то
(нижний
индекс мы пишем для напоминания о том,
по какой переменной берётся производная),
то
![]()
Тот же самый, разумеется, результат мы
получим, использовав равенство
![]() и
применив формулу производной произведения:
и
применив формулу производной произведения:
![]()
Однако первый способ гораздо продуктивнее: совершенно аналогично получаем, например,
![]()
![]()
и т. п.
Беря в качестве промежуточного аргумента
любую дифференцируемую функцию
![]() ,
из доказанных ранее формул получаем:
,
из доказанных ранее формул получаем:
|
|
|
|
в частности,
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в частности,
| |
|
|
|
Пример 4.5Найдём производную функции
![]() .
Здесь промежуточный аргумент равен
.
Здесь промежуточный аргумент равен
![]() ;
;
![]() .
Поэтому по формуле
.
Поэтому по формуле
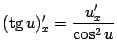 получаем:
получаем:
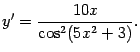
Пример 4.6Найдём производную функции
![]() .
Здесь функция имеет вид
.
Здесь функция имеет вид
![]() ,
с промежуточным аргументом
,
с промежуточным аргументом
![]() ,
который, в свою очередь, является сложной
функцией. Поэтому
,
который, в свою очередь, является сложной
функцией. Поэтому
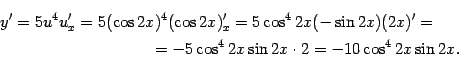
Пример 4.7Найдём производные ареа-функций (напомним, что ареа-функции -- это функции, обратные к гиперболическим функциям). Ранее мы записали для них следующие формулы:
|
|
|
|
|
|
|
(в зависимости от того, что считать
главной ветвью функции
| |
|
|
|
|
|
|
Поэтому
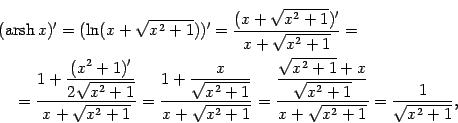
и аналогично:
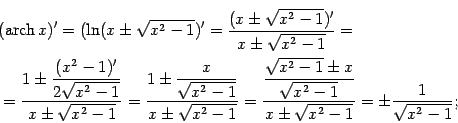
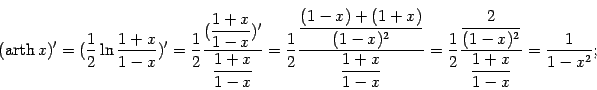
и аналогично:
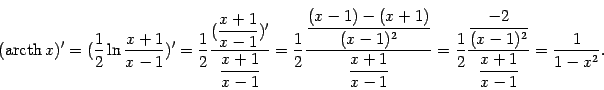
Последние две формулы не противоречат
друг другу, так как при
![]() ,
а
,
а
 при
при
![]() .
.
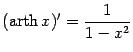
Упражнение
4.1Пусть
![]() --
чётная функция, имеющая производную
--
чётная функция, имеющая производную
![]() .
Докажите, что тогда
.
Докажите, что тогда
![]() является
нечётной функцией. Наоборот, если
является
нечётной функцией. Наоборот, если
![]() --
нечётная функция, докажите, что
--
нечётная функция, докажите, что
![]() --
чётная функция.
--
чётная функция.
При этом воспользуйтесь тем, что для
чётной функции
![]() ,
а для нечётной функции
,
а для нечётной функции
![]() ,
и примените правило нахождения производной
композиции, с промежуточным аргументом
,
и примените правило нахождения производной
композиции, с промежуточным аргументом
![]() .
.
Инвариантность дифференциала
Рассмотрим функцию
![]() .
Если предположить, что
.
Если предположить, что
![]() --
независимая переменная, то
--
независимая переменная, то
![]()
Если же рассматривать переменную
![]() как
промежуточный аргумент, зависящий от
независимого переменного
как
промежуточный аргумент, зависящий от
независимого переменного
![]() ,
то есть
,
то есть
![]() ,
то
,
то
![]() --
это композиция, и дифференциал
--
это композиция, и дифференциал
![]() можно
найти, применив формулу для производной
сложной функции:
можно
найти, применив формулу для производной
сложной функции:
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
![]()
поскольку
![]() .
Так что и в этом случае, как и в случае
независимой переменной
.
Так что и в этом случае, как и в случае
независимой переменной
![]() ,
верна формула
,
верна формула
![]() ,
только теперь
,
только теперь
![]() понимается
как дифференциал функции, а не независимого
переменного.
понимается
как дифференциал функции, а не независимого
переменного.
Тот факт, что во всех случаях, независимо
от предположения о том, чем является
переменная
![]() ,
формула
,
формула
![]() имеет
место, называетсяинвариантностью
дифференциала.
имеет
место, называетсяинвариантностью
дифференциала.
Производная обратной функции
Пусть
![]() --
непрерывная функция, монотонная на
интервале
--
непрерывная функция, монотонная на
интервале
![]() .
Тогда, как мы доказали в гл. 3, функция
.
Тогда, как мы доказали в гл. 3, функция
![]() имеет
обратную функцию
имеет
обратную функцию
![]() ,
которая также является непрерывной и
монотонной функцией на интервале
,
которая также является непрерывной и
монотонной функцией на интервале
![]() ,
в который функция
,
в который функция
![]() переводит
интервал
переводит
интервал
![]() .
Пусть
.
Пусть
![]() --
фиксированная точка и
--
фиксированная точка и
![]() --
точка, ей соответствующая. Тогда
--
точка, ей соответствующая. Тогда
![]() .
.
Теорема 4.5Пусть функция
![]() имеет
в точке
имеет
в точке
![]() производную
производную
![]() .
Тогда обратная функция
.
Тогда обратная функция
![]() имеет
в соответствующей точке
имеет
в соответствующей точке
![]() производную
производную
![]() ,
которую можно отыскать по формуле
,
которую можно отыскать по формуле
|
|
(4.14) |
Доказательство.
Дадим аргументу
![]() приращение
приращение
![]() ,
такое что
,
такое что
![]() ,
и рассмотрим соответствующее приращение
,
и рассмотрим соответствующее приращение
![]() ,
определяемое равенством
,
определяемое равенством
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() ;
при этом
;
при этом
![]() ,
а из монотонности функции
,
а из монотонности функции
![]() следует,
что
следует,
что
![]() .
Поскольку как функция
.
Поскольку как функция
![]() ,
так и функция
,
так и функция
![]() непрерывны,
то условия
непрерывны,
то условия
![]() и
и
![]() эквивалентны.
Составим теперь разностное отношение
для функции
эквивалентны.
Составим теперь разностное отношение
для функции
![]() и
запишем для него очевидное равенство:
и
запишем для него очевидное равенство:
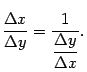
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Теперь перейдём в этом равенстве к
пределу при
![]() и
учтём, что при этом
и
учтём, что при этом
![]() тоже
стремится к 0:
тоже
стремится к 0:

что мы и хотели доказать.
Заметим, что, очевидно, из формулы (4.14) следует, что
|
|
(4.15) |
если
![]() --
функция, обратная к
--
функция, обратная к
![]() .
.
Замечание
4.10Нетрудно заметить из приведённого
доказательства, что если существует
производная
![]() ,
то разностное отношение
,
то разностное отношение
![]() стремится
к
стремится
к
![]() при
при
![]() ,
что соответствует вертикальной
касательной к графику
,
что соответствует вертикальной
касательной к графику
![]() при
при
![]() (если
считать, что ось
(если
считать, что ось
![]() расположена
горизонтально, а ось
расположена
горизонтально, а ось
![]() --
вертикально).
--
вертикально).
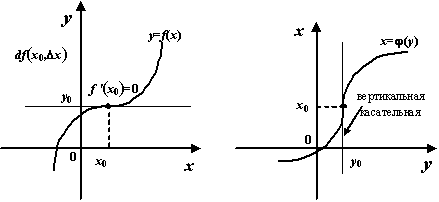
Рис.4.7.Графики
функций
![]() и
и
![]() и
касательные к ним при
и
касательные к ним при
![]()
Полученная формула для производной
обратной функции имеет прозрачный
геометрический смысл. Заметим, что
график как функции
![]() ,
так и обратной функции
,
так и обратной функции
![]() изображается
на координатной плоскости
изображается
на координатной плоскости
![]() одной
и той же линией, состоящей из точек
одной
и той же линией, состоящей из точек
![]() ,
где
,
где
![]() или,
что то же самое,
или,
что то же самое,
![]() .
Поэтому, если в точке
.
Поэтому, если в точке
![]() график
функции
график
функции
![]() имеет
касательную, образующую угол
имеет
касательную, образующую угол
![]() с
осью
с
осью
![]() ,
то угол той же касательной с осью
,
то угол той же касательной с осью
![]() будет,
очевидно, равен
будет,
очевидно, равен
![]() .
Тогда
.
Тогда
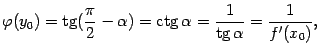
поскольку для обратной функции
![]() производная
даёт тангенс угла наклона касательной
по отношению к оси
производная
даёт тангенс угла наклона касательной
по отношению к оси
![]() ,
на которой меняется аргумент функции
,
на которой меняется аргумент функции
![]() .
.

Рис.4.8.Углы,
тангенсы которых равны
![]() и
и
![]() ,
дополняют друг друга до
,
дополняют друг друга до
![]()
Производные некоторых элементарных функций (продолжение)
Применим полученную формулу производной обратной функции (точнее, формулу (4.15)) для нахождения производных некоторых элементарных функций.
Пример 4.8Найдём производную функции
![]() .
Обратной к этой функции служит главная
ветвь функции
.
Обратной к этой функции служит главная
ветвь функции
![]() (
(
![]() ),
производная которой равна
),
производная которой равна
![]() .
Заметим, что при указанных значениях
.
Заметим, что при указанных значениях
![]() выполнено
неравенство
выполнено
неравенство
![]() ,
откуда
,
откуда
![]() (корень
берём со знаком
(корень
берём со знаком
![]() ).
Поэтому по формуле (4.15):
).
Поэтому по формуле (4.15):
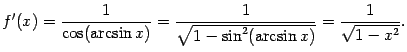
Пример 4.9Аналогично отыщем производную
функции
![]() .
Обратной к
.
Обратной к
![]() служит
главная ветвь функции
служит
главная ветвь функции
![]() (
(
![]() ),
производная которой равна
),
производная которой равна
![]() .
Заметим, что при
.
Заметим, что при
![]() выполнено
неравенство
выполнено
неравенство
![]() ,
откуда
,
откуда
![]() (корень
со знаком
(корень
со знаком
![]() ).
Поэтому по формуле (4.15)
).
Поэтому по формуле (4.15)
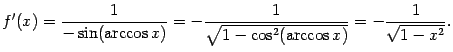
Заметим однако, что тот же результат
можно было бы гораздо легче получить,
используя тригонометрическую формулу
![]() ,
откуда
,
откуда
![]() и
и
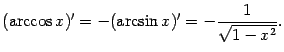
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример 4.10Найдём производную функции
![]() .
Обратной к этой функции служит главная
ветвь функции
.
Обратной к этой функции служит главная
ветвь функции
![]() (
(
![]() ),
производная которой равна
),
производная которой равна
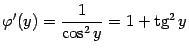 .
Поэтому по формуле (4.15)
.
Поэтому по формуле (4.15)

Пример 4.11Найдём производную функции
![]() .
Обратной к этой функции служит главная
ветвь функции
.
Обратной к этой функции служит главная
ветвь функции
![]() (
(![]() ),
производная которой равна
),
производная которой равна
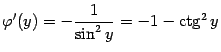 .
Поэтому по формуле (4.15)
.
Поэтому по формуле (4.15)
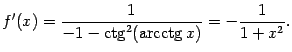
Конечно, ту же формулу можно было получить
из соотношения
![]() ,
откуда
,
откуда
![]() и
и
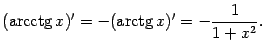
Пример 4.12Найдём производную функции
![]() (
(![]() ).
Обратной к ней служит функция
).
Обратной к ней служит функция
![]() ,
производная которой такова:
,
производная которой такова:
 .
Поэтому формула (4.15) даёт
.
Поэтому формула (4.15) даёт
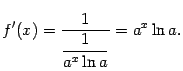
В частности, при
![]() получаем
получаем
![]()
Выведем теперь формулы для производных гиперболических функций.
Пример 4.13Пусть
![]() .
Заметим, что
.
Заметим, что
![]()
по формуле производной композиции (с
промежуточным аргументом
![]() ).
Тогда
).
Тогда
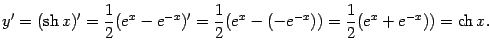
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Пример 4.14Аналогично находится производная
гиперболического косинуса
![]() :
:
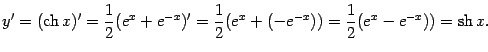
Пример 4.15Найдём производную гиперболического
тангенса
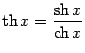 .
Заметим для начала, что
.
Заметим для начала, что
![]() (проверьте!).
Далее, имеем:
(проверьте!).
Далее, имеем:
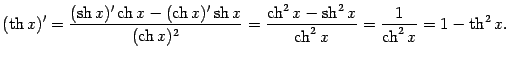
Пример 4.16Найдём производную гиперболического
котангенса
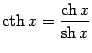 .
Имеем:
.
Имеем:
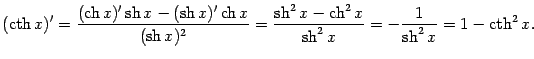
Упражнение
4.2Выведите эти же 4 формулы для
производных функций
![]() ,
исходя из того, что это -- обратные
функции к соответствующим ареа-функциям,
производные которых мы уже нашли выше.
При этом используйте формулу (4.15).
,
исходя из того, что это -- обратные
функции к соответствующим ареа-функциям,
производные которых мы уже нашли выше.
При этом используйте формулу (4.15).
Обратно, исходя из доказанных формул для производных гиперболических функций, выведите при помощи формулы (4.15) формулы для производных ареа-функций.
Пример 4.17Найдём теперь формулу для производной
функции
![]() при
произвольном вещественном
при
произвольном вещественном
![]() .
Некоторые частные случаи (при
.
Некоторые частные случаи (при
![]() ,
,
![]() )
были нами разобраны выше.
)
были нами разобраны выше.
Итак, пусть
![]() ,
,
![]() ,
,
![]() .
Запишем функцию в виде
.
Запишем функцию в виде
![]() и
найдём её производную как производную
композиции с промежуточным аргументом
и
найдём её производную как производную
композиции с промежуточным аргументом
![]() .
Получаем тогда
.
Получаем тогда
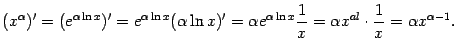
Применим теперь полученные формулы для вычисления некоторых производных.
Пример 4.18Найдём производную функции
 при
при![]()
При
![]() функция
имеет неустранимый разрыв первого рода,
поскольку
функция
имеет неустранимый разрыв первого рода,
поскольку
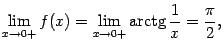
а
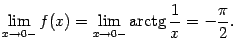
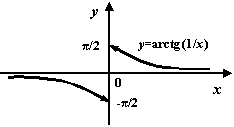
Рис.4.9.График
функции
![]()
Теперь вычислим производную при
![]() :
применяя формулу производной сложной
функции, получаем
:
применяя формулу производной сложной
функции, получаем
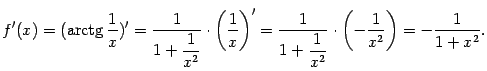
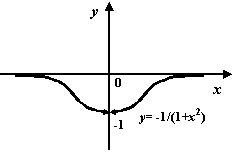
Рис.4.10.График
производной
![]()
Заметим, что если бы не разрыв при
![]() ,
эта производная совпала бы с производной
функции
,
эта производная совпала бы с производной
функции
![]() .
Это неспроста: дело в том, что если мы
положим
.
Это неспроста: дело в том, что если мы
положим

то
![]() будет
совпадать с
будет
совпадать с
![]() при
всех
при
всех
![]() .
В то же время
.
В то же время
![]() отличается
на постоянное слагаемое от
отличается
на постоянное слагаемое от
![]() при
при
![]() ,
и поэтому производные у
,
и поэтому производные у
![]() и
у
и
у
![]() одинаковые.
одинаковые.
Упражнение 4.3Найдите производную функции
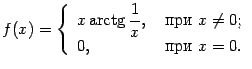
Отдельно вычислите производную при
![]() (как
производную произведения) и производные
слева и справа при
(как
производную произведения) и производные
слева и справа при
![]() (пользуясь
определением производной, как
(пользуясь
определением производной, как