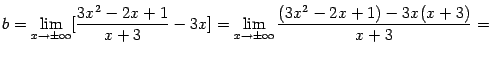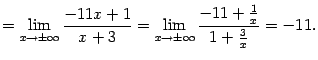Примеры исследования функций и построения графиков

        Пример 7.39Построим график функции .

1). Функция -- многочлен, а у всех многочленов область определения -- вся вещественная ось:.

2). Многочлены бывают чётными функциями, если содержат только чётные степени переменного , и нечётными функциями, если содержат только нечётные степени. Для функцииэто не так, значит,не является ни чётной, ни нечётной функцией.

Периодическими из всех многочленов бывают только постоянные, то есть не зависящие от ; в нашем случае это не так, поэтому-- не периодическая функция.

3). Вертикальных асимптот график не имеет, поскольку область определения не имеет граничных точек. (У графиков многочленов вообще не бывает вертикальных асимптот.)

4). Поскольку многочлен имеет степень 3 (а не 1 или 0), то его график не имеет наклонных или горизонтальных асимптот.

5). Пересечение с осью найдём, вычислив значениепри: имеем. Для нахождения пересечений графика с осьюследует решить уравнение. Целых корней это уравнение не имеет. Вычисляя значения в некоторых целых точках, например,

мы начинаем подозревать, что уравнение имеет только один корень , лежащий на интервале, причём ближе к точке, чем к 0. (Действительно, если применить какой-либо из методов приближённого нахождения корней алгебраического уравнения, мы получим, что. Эти методы мы изучим ниже, в главе 9. А пока нам достаточно того, что.) Заметим, чтоменяет знак снапри переходе через точку.

6). Производная данной функции равна . Найдём интервалы возрастания функции, решая неравенство. Корни квадратного трёхчлена -- это, значит, решением неравенства служит объединение интервалови. На каждом из этих интервалов функциявозрастает. Интервалы убывания задаются обратным неравенством, то есть. Его решением служит интервал. На этом интервале функция убывает.

В точке возрастание функции сменяется убыванием, значит,-- точка локального максимума. Значение функции в этой точке равно

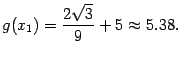
В точке убывание функции сменяется возрастанием, значит,-- точка локального минимума. Значение функции в этой точке равно

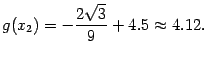
Как мы видим, на участке убывания значения функции изменяются от дои остаются положительными. Это доказывает, что сама функция действительно имеет только один корень.

7). Вторая производная функции равна . Для отыскания интервала выпуклости решим неравенство, то есть, откуда. Значит, функция выпукла на интервале. Обратное неравенстводаёт нам интервал вогнутости; очевидно, это. В точкенаправление выпуклости меняется, следовательно,-- это точка перегиба. Значение функции в этой точке равно.

8). С учётом предыдущих семи пунктов строим график функции .

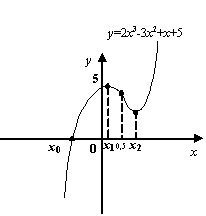
Рис.7.46.График функции CLX.ru - реклама в интернет

    

        Пример 7.40Исследуем функцию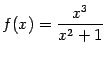и построим её график.

1). Поскольку знаменатель положителен при всех , область определения функции -- вся ось.

2). Функция -- нечётная, поскольку при смене знакачислитель меняет знак, а знаменатель остаётся без изменения, откуда. Следовательно, график функции симметричен относительно начала координат.

Периодической функция не является.

3). Поскольку область определения этой элементарной функции -- вся вещественная ось, вертикальных асимптот график не имеет.

4). Найдём наклонные асимптоты при в виде. Имеем:

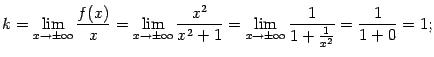
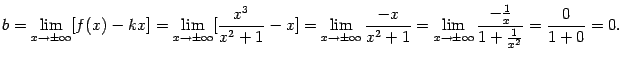
Таким образом, асимптотой как при , так и прислужит прямая.

5). Найдём точки пересечения с осями координат. Имеем: , причём-- единственное решение уравнения. Значит, графикпересекает сразу и ось, и осьв начале координат.

Очевидно, что приипри.

6). Найдём производную:

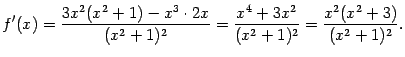
Очевидно, что при всех; единственная точка, в которой-- это. Значит, функциявозрастает на всей оси, а в стационарной точкеимеет горизонтальную касательную.

7). Найдём вторую производную:

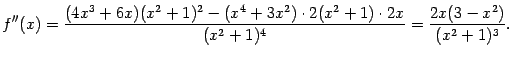
Знаменатель этой дроби положителен при всех . Числитель имеет корнии, при этомна интервалахи-- на этих интервалах функция выпукла. На интервалахивыполняется обратное неравенство, здесь функция вогнута. Все три точки, в которых, то есть точки, являются точками перегиба.

8). Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции. График имеет такой вид:

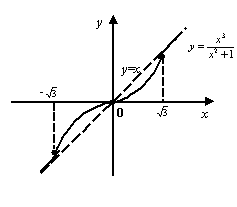
Рис.7.47.График функции

    

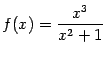
        Пример 7.41Исследуем функцию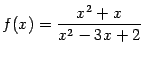и построим её график.

1). Заметим, что знаменатель имеет корни и, так что функцию можно представить в виде

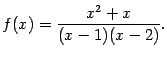
Теперь легко видеть, что области определения функции не принадлежат только точки 1 и 2:

Область значений найти без всяких вычислений мы не можем; отложим этот вопрос до нахождения локальных экстремумов.

2). Поскольку область определения не симметрична относительно точки 0, функция не может быть ни чётной, ни нечётной. Очевидно также, что она не периодична (хотя бы потому, что её область определения не имеет периодической структуры).

3). Область определения этой элементарной функции имеет две граничных точки: 1 и 2.

При значение числителя стремится к, а знаменателя -- к 0, поэтомупри. Значит, вертикальная прямая-- это вертикальная асимптота графика. При(то есть в достаточно малой левой окрестности точки 1) числитель положителен, а знаменатель состоит из двух отрицательных сомножителей, откуда следует, чтопри. Причислитель снова положителен, а в знаменателе множительположителен, аотрицателен. Получаем, чтопри.

При предел числителя равен, а знаменателя -- нулю, поэтомупри. Тем самым, вертикальная прямаяслужит второй вертикальной асимптотой графика. Причислитель положителен, а знаменатель отрицателен, поскольку, а. Отсюда следует, чтопри. Причислитель снова положителен, а в знаменателе оба множителя положительны. Получаем, чтопри.

4). Поскольку числитель и знаменатель -- многочлены одной и той же (второй) степени, то легко видеть, что имеет предел при:

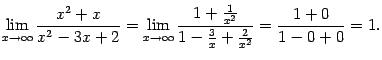
Следовательно, горизонтальная прямая служит горизонтальной асимптотой графика как при, так и при. (Искать наклонную асимптоту в видеи находитьипо общим формулам нам теперь нет никакой необходимости.)

5). Найдём точки пересечения графика с осями координат. Поскольку , то график пересекает ось(и, одновременно, ось) в начале координат.

Приравнивая числитель к нулю, получаем уравнение , которое имеет два корня:и. Значит, график пересекает осьв этих двух точках (одну из них мы уже отметили ранее).

Пользуясь методом интервалов (известным из школьной программы), определим знак функции на интервалах между корнями и точками разрыва. Таких интервалов получается пять: ;;;;.

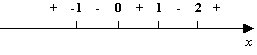
Рис.7.48.Интервалы знакопостоянства функции

На этом рисунке знаком отмечены те интервалы, на которых функция положительна, и знакомте, где она отрицательна.

6). Найдём производную:

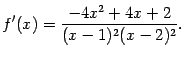
Для нахождения интервалов возрастания решим неравенство , эквивалентное квадратному неравенству(при), поскольку знаменатель принимает положительные значения. Решением квадратного неравенства служит интервал; однако точка, не входящая в, принадлежит этому интервалу. Тем самым, интервалов возрастания функциидва: этои.

Для нахождения интервалов убывания нужно решить неравенство , или(при). Решением квадратного неравенства служит, очевидно, объединение двух интервалови; точкаделит второй из них на две части. Тем самым, функцияубывает на трёх интервалах:,и.

В точке убывание функции сменяется возрастанием. При этомнепрерывна в точке, как любая элементарная функция в любой точке своей области определения. Значит,-- точка локального минимума. Значение функции в этой точке минимума равно

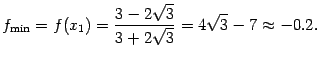
В точке возрастание функции сменяется убыванием. При этом функциянепрерывна в точке. Значит,-- точка локального максимума. Значение функции в точке максимума равно

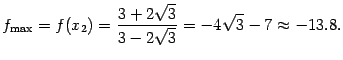
Теперь мы можем записать область значений функции: это

7). Найдём вторую производную:

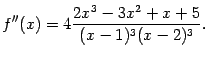
Для нахождения интервалов выпуклости нужно решить неравенство . Заметим, что числитель совпадает с функцией, рассмотренной нами в предыдущем примере. Там мы видели, чтоменяет знак при переходе через точку. Поскольку знаменатель содержит нечётные степени биномови, то они также меняют знак при переходе, соответственно, через точки 1 и 2. Итак,меняет знак при переходе через три точки:, 1 и 2. Из этих трёх точек функциянепрерывна только в точке, так что это единственная точка перегиба. Методом интервалов легко выясняем, что на интервалахифункция вогнута, а на интервалахи-- выпукла.

8). С учётом предыдущих семи пунктов строим график функции .

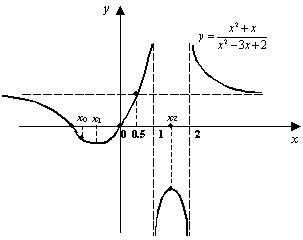
Рис.7.49.График функции

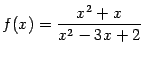
Глядя на график, замечаем, что для полноты картины хорошо бы ещё найти ту точку, где график пересекается с горизонтальной асимптотой . Для этого решим уравнение, то естьЕго решением служит число. Отметим эту точку на оси. Теперь наш чертёж отмечает все особенности графика.

        Пример 7.42Исследуем функциюи построим её график.

1). Ясно, что , поскольку оба сомножителя в выраженииопределены при любом. Область значенийнайдём после того, как отыщем локальные экстремумы функции.

2). Функция не является ни чётной, ни нечётной; не является она и периодической.

3). Область определения не имеет граничных точек, значит, нет и вертикальных асимптот графика.

4). Будем искать наклонные асимптоты в виде . Коэффициентнайдём по формуле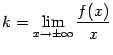: приимеем

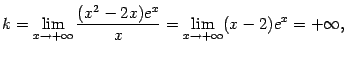
так что при асимптоты нет, причём функциястремится кпри.

При имеем:

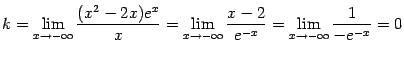
(для раскрытия неопределённости вида мы применили правило Лопиталя). Теперь найдём значениепо формуле. Имеем:

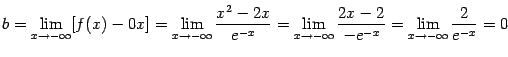
(здесь мы применили правило Лопиталя два раза подряд). Таким образом, и, так что приасимптота имеет уравнение, то есть совпадает с осью.

5). Точка пересечения с осью равна. Заодно нашли одну точку пересечения с осью. Чтобы найти все точки пересечения графика с осью, решаем уравнение. Поскольку, решаем уравнение, откуда получаем два корня:и. Так как точек разрыва нет, то имеем три интервала знакопостоянства функции:,и. Знак функции определяется множителем, посколькупри всех. Значит,прии приипри.

6). Вычислим производную:

Интервалы возрастания задаются неравенством , то есть, с учётом того, что, неравенством. Решением этого неравенства служит множествоНа этих двух интервалах функция возрастает. Легко видеть, что на интервалевыполняется неравенство, следовательно, это интервал убывания функции. В точкевозрастание сменяется убыванием, значит, точка-- точка локального максимума. Значение функции в этой точке равно

В точке убывание сменяется возрастанием, значит, точка-- точка локального минимума функции. Значение функции в точке минимума таково:

Теперь мы можем примерно представить, как идёт график функции:

Рис.7.50.Эскиз графика функции

Упражнения и задачи

        Упражнение 7.3Найдите область определения и вертикальные асимптоты графика функции

Подсказка:

Рассмотрите точки , в которых знаменатель обращается в 0. Внимание: в одной из этих точек вертикальной асимптоты нет, так как функция имеет устранимый разрыв.

Решение:

Область определения составляют все точки оси , кроме 0, и 2:

CLX.ru - реклама в интернет

Заметим теперь, что при числитель также обращается в 0:

Значит, многочлен, стоящий в числителе, делится нацело на . Деление столбиком даёт:

Значит, при дробь можно сократить на :

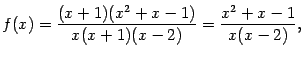
откуда видно, что при функция стремится 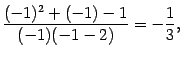к а не к .

При , равном двум другим корням знаменателя, 0 и 2, числитель в 0 не обращается, а равен и соответственно. Значит, при и при , и прямые и -- вертикальные асимптоты.

Ответ:

вертикальные асимптоты: и .

        Упражнение 7.4Найдите вертикальные асимптоты графиков функций:

а)

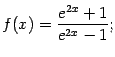
б) ;

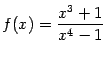в) .

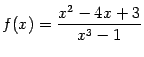Ответы:а) ; б) ; в) вертикальных асимптот нет.

        Упражнение 7.5Найдите наклонные или горизонтальные асимптоты графика функции

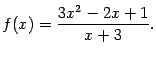
Подсказка:

Воспользуйтесь общими формулами для и в уравнении асимптоты . Пределы при и при здесь можно искать заодно.

Решение:

Найдём и :

 

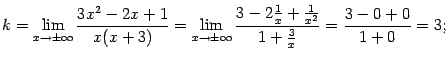
Итак, прямая служит наклонной асимптотой графика

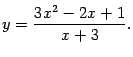
Ответ:наклонная асимптота при имеет уравнение .

        Упражнение 7.6Найдите наклонные или горизонтальные асимптоты графиков функций:

а) ;

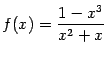б) ;

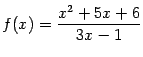в)

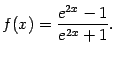
Ответы:а) при ; б) при ; в) при и при .

        Упражнение 7.7Найдите наибольшее и наименьшее значения функции на отрезке .

Подсказка:

Найдите стационарные точки функции, попадающие на заданный отрезок, и добавьте к ним концы отрезка. В одной из этих точек функция будет принимать наибольшее, а в другой -- наименьшее значение.

Решение:

Поскольку знаменатель дроби положителен при всех , функция непрерывна на всей оси . Поэтому все её критические точки -- стационарные. Найдём производную:

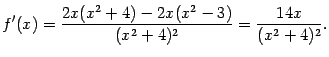
Очевидно, что производная обращается в 0 только в одной точке ; эта стационарная точка лежит на заданном отрезке .

Вычисляем значения функции в этой стационарной точке и в концах отрезка:

Выбирая из этих значений наибольшее и наименьшее, получаем ответ:

Ответ:

    

        Упражнение 7.8Найдите наибольшие и наименьшие значения функций на заданных отрезках:

а) на отрезке ;

б) 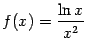на отрезке ;

в) на отрезке .

Ответы:а) ;

б) ;

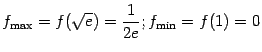в) .

        Упражнение 7.9Найдите интервалы возрастания и убывания, а также точки локального экстремума функции .

Подсказка:

Найдите производную и решите неравенства и .

Решение:

Производная равна . Неравенство имеет решение ; на этих двух интервалах возрастает. Неравенство имеет решение ; на этом интервале убывает. Следовательно, точка -- точка локального максимума, а точка -- точка локального минимума.

Ответ:

Интервалы возрастания: и ; интервал убывания: ; точка локального максимума: , точка локального минимума: .

        Упражнение 7.10Найдите интервалы возрастания и убывания и точки локальных экстремумов функций:

а) ;

б) ;

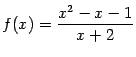в) .

Ответы:а) интервалы возрастания: и ; интервалы убывания: и ; точка локального максимума ; точки локального минимума ;

б) интервалы возрастания: и ; интервалы убывания: и ; точка локального максимума ; точка локального минимума ;

в) интервал возрастания: ; интервалы убывания: и ; точка локального минимума ; точек локального максимума нет.

        Упражнение 7.11Найдите стационарные точки функции

и определите наличие в них локального экстремума.

Подсказка:

Стационарные точки задаются уравнением . Если вторая производная в стационарной точке положительна, то это точка локального минимума, а если отрицательна, то точка локального максимума.

Решение:

Найдём производную: ; стационарные точки задаются уравнением , то есть это точки и . Вторая производная равна . Её значение в стационарных точках: ; . Следовательно, в точке -- локальный максимум, а в точках и -- локальный минимум.

Ответ:

Имеется три стационарные точки: , 0 и 1; и 1 -- точки локального минимума, а 0 -- точка локального максимума.

        Упражнение 7.12Найти стационарные точки функций и исследовать их на наличие локального экстремума:

а) ;

б) ;

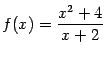в) .

Ответы:а) -- точка локального максимума; -- точка локального минимума;

б) -- точка локального максимума; -- точка локального минимума;

в) -- точка локального минимума; точек локального максимума нет.

        Упражнение 7.13Найдите интервалы выпуклости и вогнутости и точки перегиба функции

Подсказка:

Интервалы выпуклости задаются неравенством , а интервалы вогнутости -- неравенством .

Решение:

Найдём вторую производную:

Неравенство имеет решение ; на этом интервале функция выпукла. Неравенство имеет решение ; на этих двух интервалах функция вогнута.

В точках и функция меняет направление выпуклости, так что эти точки являются точками перегиба.

Ответ:

Интервал выпуклости: ; интервалы вогнутости: и ; точки перегиба: и .

        Упражнение 7.14Найдите интервалы выпуклости и вогнутости и точки перегиба следующих функций:

а) ;

б) ;

в) .

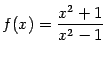Ответы:а) Интервалы выпуклости: и ; интервал вогнутости: ; точки перегиба: и .

б) Интервалы выпуклости: и ; интервал вогнутости: ; точки перегиба: и .

в) Интервалы выпуклости: и ; интервал вогнутости: ; точек перегиба нет.

        Упражнение 7.15Проведите полное исследование функций и постройте их графики (в затруднительных случаях характерные точки можно находить приближённо):

а) ;

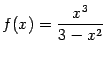б) ;

в) .

Ответы:а) Функция нечётная;

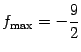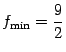вертикальные асимптоты и , наклонная асимптота . Точка локального максимума , при этом ; точка локального минимума , при этом . Единственная точка перегиба .

Рис.7.52.График функции

б) Функция чётная; ; горизонтальная асимптота . Точки локального максимума ; значение в этих точках 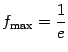; точка локального минимума . Четыре точки перегиба:

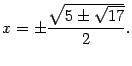
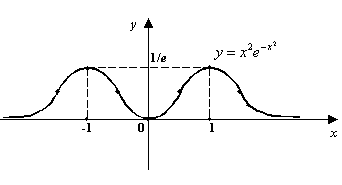
Рис.7.53.График функции

в) Функция нечётная; ; асимптоты при и при . Точка локального максимума , при этом ; точка локального минимума , при этом . Единственная точка перегиба .

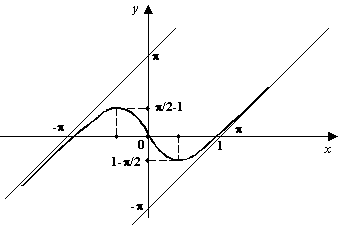
Рис.7.54.График функции