- •Функции и их графики Конспекты, лекции, задачи
- •Первый способ задания функции: табличный
- •Clx.Ru - реклама в интернет
- •Упражнения
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
- •Сводка основных результатов о производных
- •Формула Тейлора теория и практика в примерах Многочлен Тейлора
- •Исследование функций и построение графиков Асимптоты графика функции
- •Достаточные условия локального экстремума
- •Примеры исследования функций и построения графиков
Достаточные условия локального экстремума
В предыдущих примерах мы видели, что хотя необходимое условие не гарантировало наличие экстремума в критической точке, мы смогли исследовать поведение функции в окрестности этой точки и выяснить, имеется ли в ней экстремум и если да, то какого рода. Однако для выяснения этого нам пришлось иной раз прибегать к искусственным преобразованиям функции, которые во общем случае могут быть не очевидны или затруднительны. В данном разделе мы рассмотрим несколько общих теорем, позволяющих исследовать поведение функции в критической точке.
Теорема 7.5Пусть
![]() --
критическая точка функции
--
критическая точка функции![]() .
Если функция
.
Если функция![]() не
убывает в некоторой левой окрестности
не
убывает в некоторой левой окрестности![]() точки
точки![]() и
не возрастает в некоторой её правой
окрестности
и
не возрастает в некоторой её правой
окрестности![]() ,
то точка
,
то точка![]() --
точка локального максимума.
--
точка локального максимума.
Если же функция
![]() не
возрастает в некоторой левой окрестности
не
возрастает в некоторой левой окрестности![]() и
не убывает в некоторой правой окрестности
и
не убывает в некоторой правой окрестности![]() ,
то точка
,
то точка![]() --
точка локального минимума.
--
точка локального минимума.
Доказательство.
Если![]() не
убывает в
не
убывает в![]() ,
то
,
то![]() при
всех
при
всех![]() ,
поскольку из непрерывности
,
поскольку из непрерывности![]() .
Точно так же,
.
Точно так же,![]() при
всех
при
всех![]() .
Выберем из чисел
.
Выберем из чисел![]() и
и![]() наименьшее:
наименьшее:![]() и
рассмотрим симметричную окрестность
и
рассмотрим симметричную окрестность![]() .
При
.
При![]() ,
очевидно,
,
очевидно,![]() ,
то есть
,
то есть![]() --
точка локального максимума.
--
точка локального максимума.
Вторая половина утверждения теоремы
сводится к первой, если положить
![]() и
заметить, что функция
и
заметить, что функция![]() не
убывает в
не
убывает в![]() и
не возрастает в
и
не возрастает в![]() ;
локальный максимум функции
;
локальный максимум функции![]() соответствует
локальному минимуму функции
соответствует
локальному минимуму функции![]() .
.
Замечание
7.4Найденное достаточное
условие локального экстремума гарантирует
наличие экстремума в точке![]() .
Однако оно не является необходимым:
можно найти такую функцию
.
Однако оно не является необходимым:
можно найти такую функцию![]() ,
которая имеет экстремум (например,
минимум) в некоторой точке
,
которая имеет экстремум (например,
минимум) в некоторой точке![]() ,
однако не монотонна ни в какой левой
окрестности и ни в какой правой окрестности
этой точки. Примером может служить
функция
,
однако не монотонна ни в какой левой
окрестности и ни в какой правой окрестности
этой точки. Примером может служить
функция
График этой функции зажат между двумя
параболами
![]() и
и![]() и
в окрестности точки 0 имеет бесконечно
много промежутков монотонности,
разделённых стационарными точками, так
что
и
в окрестности точки 0 имеет бесконечно
много промежутков монотонности,
разделённых стационарными точками, так
что![]() не
монотонна ни на каком интервале вида
не
монотонна ни на каком интервале вида![]() или
или![]() .
В точке 0 функция непрерывна (по теореме
"о двух милиционерах") и имеет
минимум, так как при всех
.
В точке 0 функция непрерывна (по теореме
"о двух милиционерах") и имеет
минимум, так как при всех![]()
![]() .
.
Заметим кстати, что производная этой функции равна

Эта производная имеет в точке
![]() разрыв
второго рода.
разрыв
второго рода.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Теорема 7.6Пусть
![]() --
критическая точка функции
--
критическая точка функции![]() ,
и у этой функции существует производная
,
и у этой функции существует производная![]() в
некоторой проколотой окрестности
в
некоторой проколотой окрестности![]() .
Если при этом в левой окрестности
.
Если при этом в левой окрестности![]() имеет
место неравенство
имеет
место неравенство![]() ,
а в правой окрестности
,
а в правой окрестности![]() --
неравенство
--
неравенство![]() ,
то точка
,
то точка![]() --
точка локального максимума; если же в
левой окрестности выполнено неравенство
--
точка локального максимума; если же в
левой окрестности выполнено неравенство![]() ,
а в правой окрестности -- неравенство
,
а в правой окрестности -- неравенство![]() ,
то точка
,
то точка![]() --
точка локального минимума. Наконец,
если производная в левой и в правой
окрестности имеет один и тот же знак,
то точка
--
точка локального минимума. Наконец,
если производная в левой и в правой
окрестности имеет один и тот же знак,
то точка![]() не
является точкой локального экстремума.
не
является точкой локального экстремума.
Доказательство.
Доказательство первых двух утверждений
теоремы сразу же следует из предыдущей
теоремы итеоремы
7.2о связи знака производной с
возрастанием и убыванием функции: из
неравенства![]() следует
неубывание функции
следует
неубывание функции![]() ,
а из неравенства
,
а из неравенства![]() --
её невозрастание. Последнее утверждение
теоремы также очевидно.
--
её невозрастание. Последнее утверждение
теоремы также очевидно.
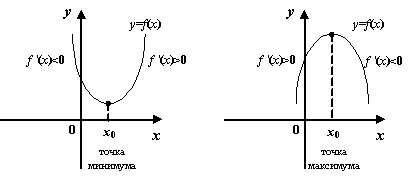
Рис.7.25.Связь смены знака производной с локальными экстремумами
Доказанную теорему можно сформулировать следующим образом:
если производная
![]() меняет
знак с
меняет
знак с![]() на
на![]() при
переходе через критическую точку
при
переходе через критическую точку![]() ,
то в этой точке -- локальный максимум
функции
,
то в этой точке -- локальный максимум
функции![]() ;
если знак производной меняется с
;
если знак производной меняется с![]() на
на![]() ,
то в точке
,
то в точке![]() --
локальный минимум; если же знак производной
при переходе через
--
локальный минимум; если же знак производной
при переходе через![]() не
изменяется, то локального экстремума
в точке
не
изменяется, то локального экстремума
в точке![]() функция
функция![]() не
имеет.
не
имеет.
Следующая теорема позволяет обойтись
для обнаружения экстремума исследованием
функции только в точке
![]() (а
не в её окрестности, как предыдущие
теоремы), но зато требует привлечения
второй производной.
(а
не в её окрестности, как предыдущие
теоремы), но зато требует привлечения
второй производной.
Теорема 7.7Пусть
![]() --
стационарная точка функции
--
стационарная точка функции![]() ,
и в этой точке существует вторая
производная
,
и в этой точке существует вторая
производная![]() ,
причём
,
причём![]() .
Тогда при
.
Тогда при![]() точка
точка![]() есть
точка локального максимума, а при
есть
точка локального максимума, а при![]() --
локального минимума.
--
локального минимума.
Доказательство.
Поскольку![]() ,
то по определению производной
,
то по определению производной
Пусть
![]() .
Тогда из существования предела следует,
что для любого
.
Тогда из существования предела следует,
что для любого![]() из
некоторой достаточно малой проколотой
окрестности
из
некоторой достаточно малой проколотой
окрестности![]() точки
точки![]() выполняется
то же неравенство для допредельного
выражения, то есть
выполняется
то же неравенство для допредельного
выражения, то есть
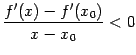
при
![]() .
Поскольку, по предположению теоремы,
.
Поскольку, по предположению теоремы,![]() --
стационарная точка, то
--
стационарная точка, то![]() ,
откуда
,
откуда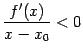 ,
то есть
,
то есть![]() имеет
знак, противоположный знаку
имеет
знак, противоположный знаку![]() :
:![]() при
при![]() и
и![]() при
при![]() .
Остаётся лишь применить теперь предыдущую
теорему, из которой следует, что
.
Остаётся лишь применить теперь предыдущую
теорему, из которой следует, что![]() --
точка локального максимума.
--
точка локального максимума.
Доказательство для случая
![]() совершенно
аналогично.
совершенно
аналогично.
Пример 7.24Рассмотрим функцию![]() .
Её производная равна
.
Её производная равна![]() ;
решая уравнение
;
решая уравнение![]() ,
находим стационарные точки функции
,
находим стационарные точки функции![]() :
это
:
это![]() .
Чтобы определить поведение функции в
этих стационарных точках, найдём вторую
производную и выясним, какой она имеет
знак в каждой из этих трёх точек. Имеем:
.
Чтобы определить поведение функции в
этих стационарных точках, найдём вторую
производную и выясним, какой она имеет
знак в каждой из этих трёх точек. Имеем:![]() .
Отсюда
.
Отсюда![]() ,
следовательно, в точке
,
следовательно, в точке![]() функция
функция![]() имеет
локальный минимум; то же в точке
имеет
локальный минимум; то же в точке![]() ,
поскольку
,
поскольку![]() также
равняется 8. В каждой из этих двух точек
значение функции равно
также
равняется 8. В каждой из этих двух точек
значение функции равно![]() .
.
В точке
![]() получаем
получаем![]() ,
поэтому в точке 0 функция
,
поэтому в точке 0 функция![]() имеет
локальный максимум. Значение
имеет
локальный максимум. Значение![]() в
этой точке равно 0.
в
этой точке равно 0.
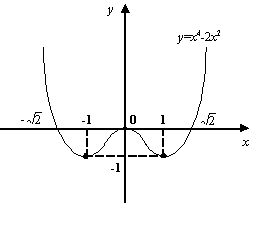
Рис.7.26.Три
локальных экстремума функции
![]()
Замечание
7.5В последней теореме
ничего не говорится о том, что происходит
в стационарной точке![]() в
случае, когда
в
случае, когда![]() .
В этом случае в точке
.
В этом случае в точке![]() может
быть как локальный экстремум (возможен
и максимум, и минимум), так и не быть
экстремума. В этом нас убеждают следующие
три примера.
может
быть как локальный экстремум (возможен
и максимум, и минимум), так и не быть
экстремума. В этом нас убеждают следующие
три примера.
Пример 7.25Функция![]() имеет
единственную стационарную точку
имеет
единственную стационарную точку![]() .
Вторая производная
.
Вторая производная![]() принимает
в этой точке значение 0, сама же функция
принимает
в этой точке значение 0, сама же функция![]() не
имеет экстремума в точке 0.
не
имеет экстремума в точке 0.
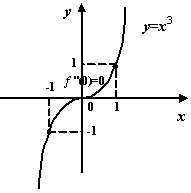
Рис.7.27.Функция
![]() не
имеет экстремума в стационарной точке
0
не
имеет экстремума в стационарной точке
0
Пример 7.26Функция![]() также
имеет единственную стационарную точку
также
имеет единственную стационарную точку![]() .
Вторая производная
.
Вторая производная![]() принимает
в этой точке значение 0, сама же функция
принимает
в этой точке значение 0, сама же функция![]() имеет
в точке 0 минимум.
имеет
в точке 0 минимум.
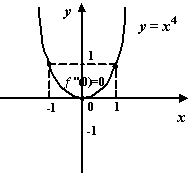
Рис.7.28.Функция
![]() имеет
минимум в стационарной точке 0, в которой
имеет
минимум в стационарной точке 0, в которой![]()
Пример 7.27Функция![]() также
имеет единственную стационарную точку
также
имеет единственную стационарную точку![]() .
Её вторая производная
.
Её вторая производная![]() принимает
в стационарной точке значение 0, а сама
функция
принимает
в стационарной точке значение 0, а сама
функция![]() имеет
в этой точке максимум.
имеет
в этой точке максимум.

Рис.7.29.Функция
![]() имеет
максимум в стационарной точке 0, в которой
имеет
максимум в стационарной точке 0, в которой![]()
Для того, чтобы разобраться в поведении
функции
![]() в
такой стационарной точке
в
такой стационарной точке![]() ,
в которой
,
в которой![]() ,
можно применить такую теорему:
,
можно применить такую теорему:
Теорема 7.8Пусть функция
![]() имеет
имеет![]() -ю
производную в некоторой окрестности
точки
-ю
производную в некоторой окрестности
точки![]() и
эта производная
и
эта производная![]() непрерывна
в точке
непрерывна
в точке![]() .
Предположим, что
.
Предположим, что
![]()
Тогда, если число
![]() --
нечётное, то в точке
--
нечётное, то в точке![]() функция
функция![]() не
имеет локального экстремума; если же
число
не
имеет локального экстремума; если же
число![]() --
чётное, то при
--
чётное, то при![]() в
точке
в
точке![]() функция
имеет локальный максимум, а при
функция
имеет локальный максимум, а при![]() --
локальный минимум.
--
локальный минимум.
Доказательство.
Для доказательства заметим, что если
разложить![]() по
формуле Тейлора в точке
по
формуле Тейлора в точке![]() с
остаточным членом в форме Лагранжа, то
получим
с
остаточным членом в форме Лагранжа, то
получим
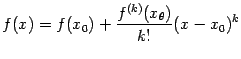
(где
![]() лежит
между
лежит
между![]() и
и![]() ),
поскольку слагаемые со степенями бинома
),
поскольку слагаемые со степенями бинома![]() ,
меньшими
,
меньшими![]() ,
имеют, по предположению, нулевые
коэффициенты. Следовательно, приращение
функции
,
имеют, по предположению, нулевые
коэффициенты. Следовательно, приращение
функции![]() можно
представить в виде
можно
представить в виде
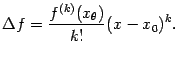
Поскольку
![]() и
и![]() непрерывна
в точке
непрерывна
в точке![]() ,
то в некоторой окрестности точки
,
то в некоторой окрестности точки![]() она
сохраняет тот же знак, что у числа
она
сохраняет тот же знак, что у числа![]() ,
в частности, знак числа
,
в частности, знак числа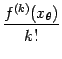 при
при![]() ,
близких к
,
близких к![]() , --
тот же, что у числа
, --
тот же, что у числа![]() .
.
Мы видим, что при нечётном
![]() приращение
приращение![]() меняет
знак при переходе через точку
меняет
знак при переходе через точку![]() ,
поскольку меняет знак множитель
,
поскольку меняет знак множитель![]() в
правой части. Значит, в этом случае
локального экстремума в точке
в
правой части. Значит, в этом случае
локального экстремума в точке![]() нет.
нет.
При чётном
![]() этот
множитель положителен при всех
этот
множитель положителен при всех![]() ,
следовательно, приращение
,
следовательно, приращение![]() (при
малых
(при
малых![]() )
имеет тот же знак, что и
)
имеет тот же знак, что и![]() :
:![]() при
при![]() (неравенство
(неравенство![]() означает,
что
означает,
что![]() --
точка локального максимума) и
--
точка локального максимума) и![]() при
при![]() (неравенство
(неравенство![]() означает,
что
означает,
что![]() --
точка локального минимума).
--
точка локального минимума).
Замечание
7.6Даже в этом усиленном
виде (теорема
7.8) достаточный признак экстремума,
связанный со значениями производных
высших порядков, не всегда отвечает на
вопрос о том, есть ли локальный экстремум
в стационарной точке. Дело в том, что,
как мы видели выше, существуют такие
функции, у которыхвсепроизводные
в некоторой точке![]() обращаются
в 0, и тем не менее функция отлична от 0
всюду, кроме этой точки. Примером может
служить функция, которую мы рассматривали
в главе 6 (замечание 6.2):
обращаются
в 0, и тем не менее функция отлична от 0
всюду, кроме этой точки. Примером может
служить функция, которую мы рассматривали
в главе 6 (замечание 6.2):
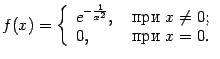
Эта функция имеет стационарную точку
![]() ,
характер которой нельзя распознать,
применивтеорему
7.8, поскольку
,
характер которой нельзя распознать,
применивтеорему
7.8, поскольку![]() при
всех
при
всех![]() .
Однако очевидно, что
.
Однако очевидно, что![]() при
всех
при
всех![]() ,
так что
,
так что![]() --
точка минимума функции
--
точка минимума функции![]() .
.
Кроме того, заметим, что может быть не
выполнено предположение о непрерывности
производной
![]() -го
порядка в точке
-го
порядка в точке![]() ,
даже если эта производная существует
при всех
,
даже если эта производная существует
при всех![]() .
В качестве примера рассмотрите
самостоятельно функцию
.
В качестве примера рассмотрите
самостоятельно функцию
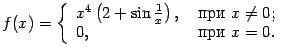
Эта функция имеет минимум (равный 0) в
точке
![]() .
Производная этой функции существует
при всех
.
Производная этой функции существует
при всех![]() и
равна
и
равна
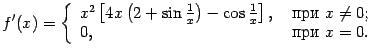
Найдите и исследуйте вторую производную этой функции.
Выпуклость функции
Определение
7.5Функция
![]() называетсявыпуклой вниз(или простовыпуклой)
на интервале
называетсявыпуклой вниз(или простовыпуклой)
на интервале
![]() ,
если график функции
,
если график функции
![]() идёт
не выше хорды, соединяющей любые две
точки графика
идёт
не выше хорды, соединяющей любые две
точки графика
![]() и
и
![]() при
при
![]() .
.
Пусть
![]() .
Тогда любую точку отрезка
.
Тогда любую точку отрезка
![]() можно
задать как
можно
задать как
![]() ,
,
![]() ,
а любую точку хорды -- как
,
а любую точку хорды -- как
![]() .
Выражение
.
Выражение
![]() задаёт
линейную функцию переменного
задаёт
линейную функцию переменного
![]() ,
график которой на отрезке
,
график которой на отрезке
![]() совпадает
с хордой.
совпадает
с хордой.
То, что график функции идёт не выше хорды, означает, что
|
|
(7.4) |
при всех
![]() .
.
Аналогично определяется выпуклость
вверх: функция
![]() называетсявыпуклой вверх(иливогнутой)
на интервале
называетсявыпуклой вверх(иливогнутой)
на интервале
![]() ,
если график функции
,
если график функции
![]() идёт
не ниже хорды, соединяющей любые две
точки графика
идёт
не ниже хорды, соединяющей любые две
точки графика
![]() и
и
![]() при
. Это означает, что
при
. Это означает, что
|
|
(7.5) |
при всех
![]() .
.
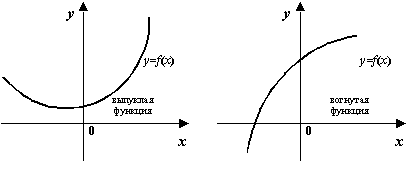
Рис.7.30.Графики
выпуклой и вогнутой функций![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
Легко видеть, что функция
![]() вогнута
на интервале
вогнута
на интервале
![]() в
том и только том случае, когда функция
в
том и только том случае, когда функция
![]() выпукла
на
выпукла
на
![]() .
.
Пример 7.28Рассмотрим функцию
![]() .
Эта функция выпукла на любом интервале
оси
.
Эта функция выпукла на любом интервале
оси
![]() .
Действительно, если интервал не содержит
точки 0, то графики
.
Действительно, если интервал не содержит
точки 0, то графики
![]() и
и
![]() на
таком интервале совпадают, откуда
следует, что неравенство (7.4) выполнено
и функция выпукла. (Заметим, что на таком
интервале верно и неравенство (7.5), так
что
на
таком интервале совпадают, откуда
следует, что неравенство (7.4) выполнено
и функция выпукла. (Заметим, что на таком
интервале верно и неравенство (7.5), так
что
![]() одновременно
и выпукла, и вогнута на таком интервале.)
Если же точка 0 лежит в интервале
одновременно
и выпукла, и вогнута на таком интервале.)
Если же точка 0 лежит в интервале
![]() ,
то
,
то
![]() и
и
![]() ,
и тот факт, что хорда лежит выше графика,
геометрически очевиден.
,
и тот факт, что хорда лежит выше графика,
геометрически очевиден.
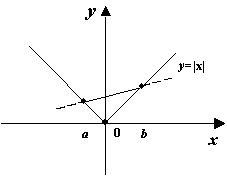
Рис.7.31.Хорда
лежит выше графика
![]()
Пример 7.29Рассмотрим функцию
![]() ;
её график -- парабола
;
её график -- парабола
![]() .
.

Рис.7.32.Функция
![]() --
выпуклая
--
выпуклая
Мы привыкли изображать параболу именно
так, что очевидно: хорда идёт выше графика
на любом интервале
![]() .
Подтвердим теперь это свойство формальной
выкладкой. Имеем:
.
Подтвердим теперь это свойство формальной
выкладкой. Имеем:
|
|
|
|
|
|
Здесь мы использовали известное
неравенство:
![]() при
всех
при
всех
![]() .
.
Теорема 7.9Пусть функция
![]() определена
на интервале
определена
на интервале
![]() и
и
![]() --
некоторая точка этого интервала. При
всех
--
некоторая точка этого интервала. При
всех
![]() определено
разностное отношение -- функция
определено
разностное отношение -- функция
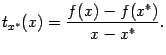
Тогда функция
![]() выпукла
на интервале
выпукла
на интервале
![]() в
том и только том случае, когда функция
в
том и только том случае, когда функция
![]() не
убывает на множестве
не
убывает на множестве
![]() .
.
Замечание
7.7Функция
![]() равна
тангенсу угла наклона хорды, одним из
концов которой служит фиксированная
точка
равна
тангенсу угла наклона хорды, одним из
концов которой служит фиксированная
точка
![]() ,
а вторым концом -- переменная точка
графика
,
а вторым концом -- переменная точка
графика
![]() .
Тем самым, теорема означает, что у
выпуклых функций угловые коэффициенты
хорд графика не убывают, где бы ни был
фиксирован один из концов хорды.
.
Тем самым, теорема означает, что у
выпуклых функций угловые коэффициенты
хорд графика не убывают, где бы ни был
фиксирован один из концов хорды.
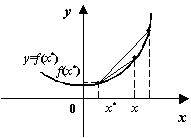
Рис.7.33.Угловой коэффициент хорды с фиксированным концом возрастает, если функция выпукла
Заметим также, что функция
![]() имеет
следующее свойство:
имеет
следующее свойство:
|
|
(7.6) |
Действительно,
|
|
|
Доказательствотеоремы 7.9. Выберем любые
две точки
![]() .
Предположим, что
.
Предположим, что
![]() (случаи
иного расположения точек
(случаи
иного расположения точек
![]() рассматриваются
аналогично). Поскольку
рассматриваются
аналогично). Поскольку
![]() ,
то
,
то
![]() при
некотором
при
некотором
![]() .
Нетрудно видеть, что тогда
.
Нетрудно видеть, что тогда
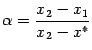 и
и
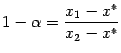 .
Поэтому из выпуклости функции
.
Поэтому из выпуклости функции
![]() следует,
что
следует,
что
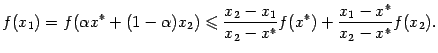
Умножая на
![]() ,
получаем:
,
получаем:
![]()
Теперь вычтем
![]() из
обеих частей неравенства. Получим, после
раскрытия скобок в правой части и
приведения подобных членов:
из
обеих частей неравенства. Получим, после
раскрытия скобок в правой части и
приведения подобных членов:
![]()
Теперь разделим обе части неравенства
на
![]() и
и
![]() и
получим:
и
получим:
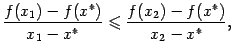
то есть
![]()
Это означает, что функция
![]() --
неубывающая.
--
неубывающая.
Доказательство того, что из неубывания
функции
![]() следует
выпуклость функции
следует
выпуклость функции
![]() ,
можно провести, если проделать все
преобразования в обратном порядке.
,
можно провести, если проделать все
преобразования в обратном порядке.
Замечание 7.8Очевидно, что аналогично доказывается следующее утверждение:
функция
![]() вогнута
на интервале
вогнута
на интервале
![]() тогда
и только тогда, когда при любом
тогда
и только тогда, когда при любом
![]() функция
функция
![]() не
возрастает на множестве
не
возрастает на множестве
![]() .
.
Доказанная теорема содержит хотя и важный, но всё же вспомогательный результат. На её основании мы получим следующее утверждение, которое уже гораздо удобнее применять на практике для исследования выпуклости.
Теорема
7.10Пусть функция
![]() имеет
на
имеет
на
![]() производную
производную
![]() .
Функция
.
Функция
![]() выпукла
на
выпукла
на
![]() тогда
и только тогда, когда производная
тогда
и только тогда, когда производная
![]() не
убывает на
не
убывает на
![]() .
.
Доказательство.
Пусть
![]() --
выпуклая функция. Возьмём точки
--
выпуклая функция. Возьмём точки
![]() на
интервале
на
интервале
![]() так,
чтобы они следовали в таком порядке:
так,
чтобы они следовали в таком порядке:
![]() .
По предыдущей теореме, функции
.
По предыдущей теореме, функции
![]() и
и
![]() не
убывают. Пользуясь также свойством
(7.6), получаем цепочку:
не
убывают. Пользуясь также свойством
(7.6), получаем цепочку:
![]()
В итоге получили, что
![]() ,
или
,
или
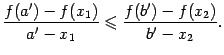
Перейдем в левой части к пределу при
![]() ,
а затем в правой части при
,
а затем в правой части при
![]() .
Так как, по предположению, производная
в точках
.
Так как, по предположению, производная
в точках
![]() и
и
![]() существует,
то односторонние пределы существуют и
равны производным в соответствующих
точках, то есть
существует,
то односторонние пределы существуют и
равны производным в соответствующих
точках, то есть
![]() .
Ввиду того, что точки
.
Ввиду того, что точки
![]() и
и
![]() можно
было выбирать произвольно, это означает,
что
можно
было выбирать произвольно, это означает,
что
![]() не
убывает на
не
убывает на
![]() .
.
Пусть теперь производная
![]() --
неубывающая функция. Фиксируем точку
--
неубывающая функция. Фиксируем точку
![]() и
найдём производную функции
и
найдём производную функции
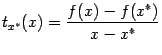 при
при
![]() .
Она равна
.
Она равна
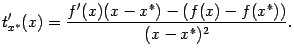
По формуле конечных приращений мы можем
представить
![]() в
виде
в
виде
![]()
где
![]() --
некоторая точка, лежащая между
--
некоторая точка, лежащая между
![]() и
и
![]() .
Заметим, что при этом знак разности
.
Заметим, что при этом знак разности
![]() --
тот же, что у разности
--
тот же, что у разности
![]() .
Получаем, что
.
Получаем, что
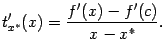
Так как
![]() --
неубывающая функция, то
--
неубывающая функция, то
![]() при
при
![]() и,
следовательно, при
и,
следовательно, при
![]() и
и
![]() при
при
![]() и,
следовательно, при
и,
следовательно, при
![]() .
В любом случае отношение неотрицательно,
то есть
.
В любом случае отношение неотрицательно,
то есть
![]() .
По теореме 7.2 отсюда следует, что функция
.
По теореме 7.2 отсюда следует, что функция
![]() не
убывает, а по теореме 7.9 -- что функция
не
убывает, а по теореме 7.9 -- что функция
![]() выпукла.
выпукла.
Замечание 7.9Разумеется, верно следующее утверждение, аналогичное доказанной теореме:
дифференцируемая функция
![]() вогнута
на интервале
вогнута
на интервале
![]() тогда
и только тогда, когда её производная
тогда
и только тогда, когда её производная
![]() не
возрастает.
не
возрастает.
Если функция имеет во всех точках
интервала вторую производную
![]() ,
то для исследования выпуклости можно
воспользоваться следующим утверждением,
которое вытекает из доказанной теоремы.
,
то для исследования выпуклости можно
воспользоваться следующим утверждением,
которое вытекает из доказанной теоремы.
Теорема
7.11Пусть на интервале
![]() функция
функция
![]() имеет
вторую производную
имеет
вторую производную
![]() .
Функция
.
Функция
![]() выпукла
на
выпукла
на
![]() тогда
и только тогда, когда
тогда
и только тогда, когда
![]() при
всех
при
всех
![]() ,
и вогнута тогда и только тогда, когда
,
и вогнута тогда и только тогда, когда
![]() при
всех
при
всех
![]() .
.
Доказательство.
Производная
![]() не
убывает на
не
убывает на
![]() в
том и только том случае, когда
в
том и только том случае, когда
![]() при
всех
при
всех
![]() ,
и не возрастает в на
,
и не возрастает в на
![]() в
том и только том случае, когда
в
том и только том случае, когда
![]() при
всех
при
всех
![]() .
Поэтому утверждение теоремы сразу
следует из теоремы 7.10 и замечания 7.9.
.
Поэтому утверждение теоремы сразу
следует из теоремы 7.10 и замечания 7.9.
Именно эту теорему чаще всего применяют для исследования выпуклости и вогнутости функции на заданном интервале, а также для нахождения интервалов выпуклости и интервалов вогнутости данной функции.
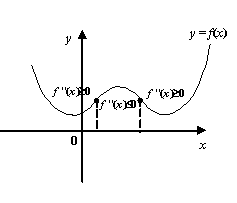
Рис.7.34.![]() на интервалах выпуклости и
на интервалах выпуклости и
![]() на
интервалах вогнутости
на
интервалах вогнутости
Пример 7.30Рассмотрим функцию
![]() ,
то есть
,
то есть
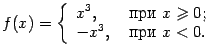
Для этой функции
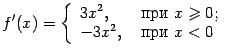
(проверьте отдельно, что производная
при
![]() существует
и равна 0) и
существует
и равна 0) и
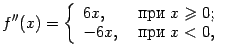
то есть
![]() .
(Также проверьте, что производная в
точке 0 существует и равна 0.) Итак,
.
(Также проверьте, что производная в
точке 0 существует и равна 0.) Итак,
![]() при
всех
при
всех
![]() ;
отсюда следует, что функция
;
отсюда следует, что функция
![]() выпукла
на всей оси.
выпукла
на всей оси.
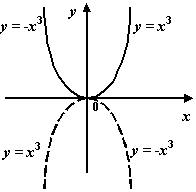
Рис.7.35.Функция
![]() выпукла
на всей оси
выпукла
на всей оси
Пример 7.31Рассмотрим функцию примера 7.24:
![]() .
Её производная равна
.
Её производная равна
![]() ;
вторая производная
;
вторая производная
![]() .
Чтобы найти интервалы выпуклости, решим
неравенство
.
Чтобы найти интервалы выпуклости, решим
неравенство
![]() ,
то есть
,
то есть
![]() .
Решением является объединение лучей:
.
Решением является объединение лучей:
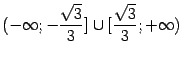 .
Значит, на интервалах
.
Значит, на интервалах
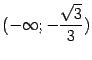 и
и
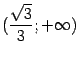 функция
функция
![]() выпукла.
выпукла.
Для нахождения интервала вогнутости
нужно решить неравенство
![]() ,
то есть
,
то есть
![]() .
Решением является отрезок
.
Решением является отрезок
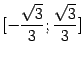 .
Значит, на интервале
.
Значит, на интервале
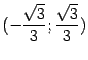 функция
функция
![]() вогнута.
вогнута.
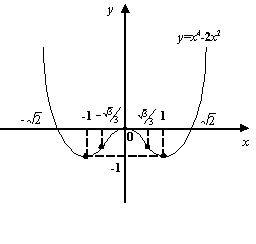
Рис.7.36.Интервалы
выпуклости и вогнутости функции
![]()
Выпуклые функции обладают следующим весьма важным свойством: они могут иметь не более одного локального минимума на интервале выпуклости. А именно, верна следующая теорема.
Теорема
7.12Пусть
![]() --
выпуклая на
--
выпуклая на
![]() функция
и
функция
и
![]() --
точка локального минимума функции
--
точка локального минимума функции
![]() .
Тогда
.
Тогда
![]()
Замечание
7.10Теорема не означает, что функция
не может иметь много точек локального
минимума, однако утверждает, что во всех
таких точках выпуклая функция принимает
одно и то же значение
![]()
Доказательствотеоремы. Пусть
![]() и
и
![]() --
две различные точки локального минимума
функции
--
две различные точки локального минимума
функции
![]() ,
причём
,
причём
![]() и
и
![]() (случай
(случай
![]() разбирается
аналогично). Положим
разбирается
аналогично). Положим
![]() и
рассмотрим линейную функцию
и
рассмотрим линейную функцию
![]() ,
на графике которой лежит хорда, соединяющая
точки
,
на графике которой лежит хорда, соединяющая
точки
![]() и
и
![]() .
Так как функция
.
Так как функция
![]() выпукла,
то
выпукла,
то
![]() при
всех
при
всех
![]() ,
то есть при всех
,
то есть при всех
![]() .
Это неравенство верно, в том числе, и
при любом
.
Это неравенство верно, в том числе, и
при любом
![]() из
некоторой правой окрестности точки
из
некоторой правой окрестности точки
![]() ,
то есть при
,
то есть при
![]() ,
,
![]() .
Тем самым получаем для таких
.
Тем самым получаем для таких
![]() :
:
![]()
Однако это противоречит тому, что
![]() --
точка локального минимума (из того, что
--
точка локального минимума (из того, что
![]() --
точка локального минимума, следует, что
при достаточно малом
--
точка локального минимума, следует, что
при достаточно малом
![]() при
при
![]() имеет
место неравенство
имеет
место неравенство
![]() ).
).
Значит, предположение о том, что
![]() ,
не может быть верным. Точно так же
доказывается, что неверно и предположение
о том, что
,
не может быть верным. Точно так же
доказывается, что неверно и предположение
о том, что
![]() .
Следовательно,
.
Следовательно,
![]() ,
то есть во всех точках локального
экстремума (если их не одна) функция
,
то есть во всех точках локального
экстремума (если их не одна) функция
![]() принимает
одно и то же значение.
принимает
одно и то же значение.
Тем самым, если о функции
![]() известно,
что она выпукла, и мы нашли некоторую
точку локального минимума
известно,
что она выпукла, и мы нашли некоторую
точку локального минимума
![]() ,
то значение в этой точке -- это
минимальное значение функции на всём
рассматриваемом интервале:
,
то значение в этой точке -- это
минимальное значение функции на всём
рассматриваемом интервале:
![]() .
Если нас интересует лишь это минимальное
значение, а не полный набор точек
минимума, то мы можем других точек
локального минимума не искать.
.
Если нас интересует лишь это минимальное
значение, а не полный набор точек
минимума, то мы можем других точек
локального минимума не искать.
Замечание 7.11Свойство, аналогичное доказанной теореме, верно и для максимумов вогнутых функций:
если
![]() --
вогнутая функция на интервале
--
вогнутая функция на интервале
![]() и
и
![]() --
точки локального максимума, то
--
точки локального максимума, то
![]()
Для доказательства достаточно вспомнить,
что
![]() --
выпуклая функция и что
--
выпуклая функция и что
![]() .
.
Замечание
7.12Теорема 7.11 проясняет тот факт,
что условие
![]() достаточно
для наличия локального минимума в
стационарной точке
достаточно
для наличия локального минимума в
стационарной точке
![]() функции
функции
![]() .
Действительно, из условия
.
Действительно, из условия
![]() следует,
что функция
следует,
что функция
![]() выпукла,
то есть её график
выпукла,
то есть её график
![]() "провисает
вниз" в окрестности точки
"провисает
вниз" в окрестности точки
![]() ,
в которой график имеет горизонтальную
касательную.
,
в которой график имеет горизонтальную
касательную.
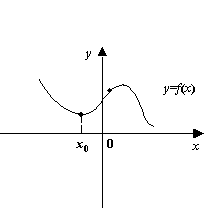
Рис.7.37.Выпуклость функции в окрестности точки минимума
Аналогично, график гладкой функции
имеет выпуклость вверх в окрестности
точки локального максимума. Поэтому
неравенство
![]() даёт
достаточное условие локального максимума.
даёт
достаточное условие локального максимума.
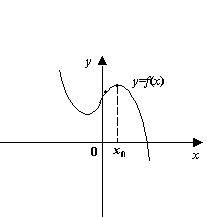
Рис.7.38.Вогнутость функции в окрестности точки максимума
Изучим теперь связь выпуклости и
вогнутости функции
![]() с
взаимным расположением графика функции
и касательных, проведённых к этому
графику.
с
взаимным расположением графика функции
и касательных, проведённых к этому
графику.
Теорема
7.13Пусть функция
![]() имеет
на интервале
имеет
на интервале
![]() производную
производную
![]() .
Функция
.
Функция
![]() выпукла
на
выпукла
на
![]() тогда
и только тогда, когда график
тогда
и только тогда, когда график
![]() лежит
(при
лежит
(при
![]() )
не ниже любой касательной
)
не ниже любой касательной
![]() ,
проведённой при любом
,
проведённой при любом
![]() ,
то есть выполняется неравенство
,
то есть выполняется неравенство
![]()
при всех
![]() .
.

Рис.7.39.График выпуклой функции идёт не ниже любой своей касательной
Доказательство. Применяя формулу конечных приращений, получаем:
![]()
где
![]() лежит
между
лежит
между
![]() и
и
![]() .
Но по теореме 7.10 производная выпуклой
функции не убывает, так что
.
Но по теореме 7.10 производная выпуклой
функции не убывает, так что
![]() при
при
![]() и
и
![]() при
при
![]() .
В любом случае получаем, что произведение
.
В любом случае получаем, что произведение
![]() неотрицательно,
откуда
неотрицательно,
откуда
![]() .
Отсюда следует неравенство из утверждения
теоремы.
.
Отсюда следует неравенство из утверждения
теоремы.
Замечание 7.13Очевидно, что для вогнутых функций верно аналогичное утверждение:
дифференцируемая функция вогнута на
интервале
![]() тогда
и только тогда, когда её график идёт не
выше любой касательной:
тогда
и только тогда, когда её график идёт не
выше любой касательной:
![]()
при всех
![]() .
.
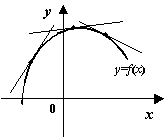
Рис.7.40.График вогнутой функции идёт не выше любой своей касательной
Определение
7.6Точкой перегибафункции
![]() называется
такая точка
называется
такая точка
![]() ,
которая разделяет два интервала
,
которая разделяет два интервала
![]() и
и
![]() ,
на одном из которых функция является
выпуклой, а на другом -- вогнутой.
,
на одном из которых функция является
выпуклой, а на другом -- вогнутой.
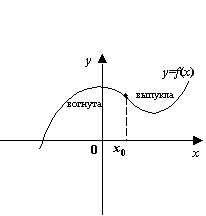
Рис.7.41.Точка перегиба разделяет интервалы с разным направлением выпуклости
В случае, если вторая производная
![]() непрерывна,
в точке перегиба
непрерывна,
в точке перегиба
![]() непременно
должно выполняться равенство
непременно
должно выполняться равенство
![]() ,
поскольку, согласно теореме 7.11,
,
поскольку, согласно теореме 7.11,
![]() должна
менять знак при переходе через точку
должна
менять знак при переходе через точку
![]() .
Верно даже несколько более сильное
утверждение:
.
Верно даже несколько более сильное
утверждение:
Теорема
7.14Пусть
![]() --
точка перегиба функции
--
точка перегиба функции
![]() ,
причём существует
,
причём существует
![]() .
Тогда
.
Тогда
![]() .
.
Доказательство.
Из существования
![]() следует,
что
следует,
что
![]() существует
при
существует
при
![]() из
некоторого интервала
из
некоторого интервала
![]() ,
окружающего точку
,
окружающего точку
![]() .
По предположению, при достаточно малом
.
По предположению, при достаточно малом
![]() ,
на интервалах
,
на интервалах
![]() и
и
![]() направление
выпуклости функции разное; пусть для
определённости
направление
выпуклости функции разное; пусть для
определённости
![]() выпукла
на
выпукла
на
![]() и
вогнута на
и
вогнута на
![]() .
Тогда функция
.
Тогда функция
![]() не
убывает на
не
убывает на
![]() и
не возрастает на
и
не возрастает на
![]() ,
согласно теореме 7.10 и замечанию 7.9.
Значит,
,
согласно теореме 7.10 и замечанию 7.9.
Значит,
 при
при
![]() и
и
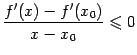 при
при
![]() .
Переходя в этих двух неравенствах к
пределу при базе
.
Переходя в этих двух неравенствах к
пределу при базе
![]() и
и
![]() соответственно
и замечая, что оба предела равны
соответственно
и замечая, что оба предела равны
![]() ,
получаем, что одновременно
,
получаем, что одновременно
![]() и
и
![]() .
Значит,
.
Значит,
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Заметим однако, что не любая точка
![]() ,
такая что
,
такая что
![]() ,
обязана быть точкой перегиба: при
переходе через такую точку функция
,
обязана быть точкой перегиба: при
переходе через такую точку функция
![]() может
и не сменить знак, тогда перегиба в точке
может
и не сменить знак, тогда перегиба в точке
![]() нет.
нет.
Пример 7.32Рассмотрим функцию
![]() ;
её вторая производная
;
её вторая производная
![]() равна
равна
![]() и
равняется 0 при
и
равняется 0 при
![]() .
Однако поскольку
.
Однако поскольку
![]() при
всех
при
всех
![]() ,
функция
,
функция
![]() выпукла
на всей оси
выпукла
на всей оси
![]() ,
согласно теореме 7.11. Точка 0 не разделяет
здесь интервалы разного направления
выпуклости.
,
согласно теореме 7.11. Точка 0 не разделяет
здесь интервалы разного направления
выпуклости.

Рис.7.42.Точка
0 не разделяет интервалы разного
направления выпуклости функции
![]()
Пример 7.33Рассмотрим функцию
![]() .
Тогда
.
Тогда
![]() и
и
![]() при
при
![]() и
и
![]() при
при
![]() .
Точка
.
Точка
![]() (в
которой
(в
которой
![]() )
разделяет интервал вогнутости
)
разделяет интервал вогнутости
![]() и
интервал выпуклости
и
интервал выпуклости
![]() .
Значит,
.
Значит,
![]() --
точка перегиба функции
--
точка перегиба функции
![]() .
.
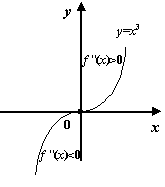
Рис.7.43.Точка
0 -- точка перегиба функции
![]()
Пример 7.34Рассмотрим функцию
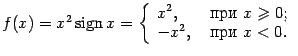 Тогда
Тогда
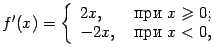 и
и
 (при
(при
![]() вторая
производная не существует). Тогда
вторая
производная не существует). Тогда
![]() при
при
![]() и
и
![]() при
при
![]() .
Точка
.
Точка
![]() (в
которой
(в
которой
![]() не
существует) разделяет интервал вогнутости
не
существует) разделяет интервал вогнутости
![]() и
интервал выпуклости
и
интервал выпуклости
![]() .
Значит,
.
Значит,
![]() --
точка перегиба.
--
точка перегиба.
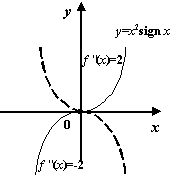
Рис.7.44.Точка
0 -- точка перегиба функции
![]()
Пример 7.35Рассмотрим функцию
![]() .
Тогда
.
Тогда
 (проверьте,
что это так!). При
(проверьте,
что это так!). При
![]() вторая
производная (как и первая) не существует.
Однако снова
вторая
производная (как и первая) не существует.
Однако снова
![]() при
при
![]() и
и
![]() при
при
![]() .
Значит,
.
Значит,
![]() --
точка перегиба.
--
точка перегиба.

Рис.7.45.Точка
0 -- точка перегиба функции
![]()
Упражнение
7.2Проверьте, пользуясь определением
точки перегиба, что если
![]() --
линейная функция (
--
линейная функция (![]() ),
то любая точка
),
то любая точка
![]() есть
её точка перегиба.
есть
её точка перегиба.
Проверьте, что любая точка
![]() (в
том числе
(в
том числе
![]() )
есть точка перегиба функции
)
есть точка перегиба функции
![]() .
.
Итак, точки перегиба содержатся в списке
тех точек
![]() ,
в которых либо
,
в которых либо
![]() ,
либо
,
либо
![]() не
существует. Однако такая точка
не
существует. Однако такая точка
![]() может
и не оказаться точкой перегиба; для
выяснения нужно исследовать поведение
функции слева и справа от "подозрительной"
точки
может
и не оказаться точкой перегиба; для
выяснения нужно исследовать поведение
функции слева и справа от "подозрительной"
точки
![]() .
.
Общая схема исследования функции и построения её графика
После того как мы обсудили многие аспекты поведения функции и способы их исследования, сформулируем общую схему исследования функции. Эта схема даст нам практический способ построения графика функции, отражающего основные черты её поведения.
Пусть дана функция
![]() .
Для её исследования нужно:
.
Для её исследования нужно:
1). Найти её область определения
![]() .
Если это не слишком сложно, то полезно
найти также область значений
.
Если это не слишком сложно, то полезно
найти также область значений
![]() .
(Однако, во многих случаях, вопрос
нахождения
.
(Однако, во многих случаях, вопрос
нахождения
![]() откладывается
до нахождения экстремумов функции.)
откладывается
до нахождения экстремумов функции.)
2). Выяснить общие свойства функции,
которые помогут в определении её
поведения: не является ли функция чётной
либо нечётной (быть может, после сдвига
влево или вправо по оси
![]() ),
не является ли она периодической.
),
не является ли она периодической.
3). Выяснить, как ведёт себя функция при
приближении аргумента
![]() к
граничным точкам области определения
к
граничным точкам области определения
![]() ,
если такие граничные точки имеются. При
этом могут обнаружиться вертикальные
асимптоты. Если функция имеет такие
точки разрыва, в которых она определена,
то эти точки тоже проверить на наличие
вертикальных асимптот функции. Поясним
сказанное примером:
,
если такие граничные точки имеются. При
этом могут обнаружиться вертикальные
асимптоты. Если функция имеет такие
точки разрыва, в которых она определена,
то эти точки тоже проверить на наличие
вертикальных асимптот функции. Поясним
сказанное примером:
Пример 7.36Пусть
 Эта
функция определена на всей числовой
оси, однако 0 является точкой разрыва
функции: при
Эта
функция определена на всей числовой
оси, однако 0 является точкой разрыва
функции: при
![]() функция
стремится к
функция
стремится к
![]() .
Значит, вертикальная прямая
.
Значит, вертикальная прямая
![]() служит
вертикальной асимптотой функции, хотя
функция и определена в точке
служит
вертикальной асимптотой функции, хотя
функция и определена в точке
![]() .
.
4). Если область определения
![]() вклоючает
в себя лучи вида
вклоючает
в себя лучи вида
![]() или
или
![]() ,
то можно попытаться найти наклонные
асимптоты (или горизонтальные асимптоты)
при
,
то можно попытаться найти наклонные
асимптоты (или горизонтальные асимптоты)
при
![]() или
или
![]() соответственно.
соответственно.
5). Найти точку пересечения графика с
осью
![]() (если
(если
![]() ).
Для этого нужно вычислить значение
).
Для этого нужно вычислить значение
![]() .
Найти также точки пересечения графика
с осью
.
Найти также точки пересечения графика
с осью
![]() ,
для чего найти корни уравнения
,
для чего найти корни уравнения
![]() (или
убедиться в отсутствии корней). Уравнение
(или
убедиться в отсутствии корней). Уравнение
![]() часто
удаётся решить лишь приближённо, но уже
отделение корней помогает лучше уяснить
строение графика. Далее, нужно определить
знак функции на промежутках между
корнями и точками разрыва.
часто
удаётся решить лишь приближённо, но уже
отделение корней помогает лучше уяснить
строение графика. Далее, нужно определить
знак функции на промежутках между
корнями и точками разрыва.
6). Найти интервалы монотонности функции
![]() (то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной
(то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной
![]() .
.
![]()
![]() CLX.ru
- реклама в интернет
CLX.ru
- реклама в интернет
На стыках интервалов монотонности найти точки локального экстремума; вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.
7). Найти интервалы выпуклости и вогнутости
функции. Это делается с помощью
исследования знака второй производной
![]() .
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции.
.
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции.
8). В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
После выяснения свойств функции, упомянутых в пунктах 1 - 8, и нахождения опорных точек (точек пересечения с осями координат, точек графика, соответствующих точкам локального экстремума, точкам перегиба и проч.) мы можем достаточно точно построить график.
Обсудим теперь подробнее некоторые из этих пунктов.
1). Область определения функции.В
некоторых примерах область определения
![]() задаётся
в самом условии задачи, например:
"Построить график функции, заданной
при
задаётся
в самом условии задачи, например:
"Построить график функции, заданной
при
![]() ".
Однако часто функция задаётся некоторой
формулой, выражающей
".
Однако часто функция задаётся некоторой
формулой, выражающей
![]() как
элементарную функцию, вроде:
как
элементарную функцию, вроде:
![]()
В таком случае принято считать, что
областью определения служит максимально
широкое множество значений
![]() ,
при которых правая часть формулы
,
при которых правая часть формулы
![]() имеет
смысл.
имеет
смысл.
Из этого соглашения по умолчанию есть
одно исключение. Если функция имеет вид
![]() или
содержит выражения такого рода, то
принято считать, что выражение
или
содержит выражения такого рода, то
принято считать, что выражение
![]() должно
быть положительно, если
должно
быть положительно, если
![]() принимает
значения любого знака, или
принимает
значения любого знака, или
![]() неотрицательно,
если
неотрицательно,
если
![]() положительно.
При этом игнорируется тот факт, что
выражение
положительно.
При этом игнорируется тот факт, что
выражение
![]() может
иметь смысл и при некоторых других
(исключительных) значениях
может
иметь смысл и при некоторых других
(исключительных) значениях
![]() и
и
![]() ,
например, когда
,
например, когда
![]() и
и
![]() принимает
целое значение.
принимает
целое значение.
Пример 7.37Для функции
![]() считаем,
что
считаем,
что
![]() ,
хотя правая часть имеет смысл также при
всех целых отрицательных
,
хотя правая часть имеет смысл также при
всех целых отрицательных
![]() .
.
Замечание 7.14При исследовании некоторых функций подробное исследование области определения мы вынуждены будем пропустить или ограничиться общими рассуждениями, ввиду сложности точного решения вопроса.
Например, область определения функции
![]() задаётся
как решение неравенства
задаётся
как решение неравенства
![]() .
Однако решить это неравенство "точно",
то есть найти выражения через радикалы
от известных чисел для точек, задающих
левые и правые концы интервалов (или
интервала?) области определения,
по-видимому, невозможно. Можно лишь
сказать, что решение будет заведомо
содержать целиком луч вида
.
Однако решить это неравенство "точно",
то есть найти выражения через радикалы
от известных чисел для точек, задающих
левые и правые концы интервалов (или
интервала?) области определения,
по-видимому, невозможно. Можно лишь
сказать, что решение будет заведомо
содержать целиком луч вида
![]() при
некотором
при
некотором
![]() ;
кроме того, непосредственная проверка
показывает, что точки
;
кроме того, непосредственная проверка
показывает, что точки
![]() и
0, например, принадлежат
и
0, например, принадлежат
![]() ,
а точка
,
а точка
![]() --
нет. Более точно можно описать
--
нет. Более точно можно описать
![]() ,
найдя корни уравнения
,
найдя корни уравнения
![]() приближённо,
с достаточно малой погрешностью, и
исследовав знак функции
приближённо,
с достаточно малой погрешностью, и
исследовав знак функции
![]() между
этими корнями.
между
этими корнями.
Способы приближённого отыскания корней алгебраических уравнений мы обсудим ниже, в главе 9.
2). Особые свойства функции.Не любая
функция обладает такими свойствами,
как чётность либо нечётность. Функция
заведомо не является ни чётной, ни
нечётной, если её область определения
несимметрична относительно точки 0 на
оси
![]() .
Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.
.
Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.
Так что если, например, при рассмотрении предыдущего пункта выяснилось, что область определения не обладает свойством симметричности либо периодичности, то заниматься исследованием соответствующих особых свойств функции нет нужды.
3). Вертикальные асимптоты.Если
функция
![]() --
элементарная, то на всех интервалах
области определения
--
элементарная, то на всех интервалах
области определения
![]() функция
функция
![]() непрерывна.
Значит, вертикальные асимптоты могут
появиться только на границах интервалов,
составляющих
непрерывна.
Значит, вертикальные асимптоты могут
появиться только на границах интервалов,
составляющих
![]() .
.
Однако не на каждой из границ этих
интервалов непременно возникает
вертикальная асимптота: например,
функция
![]() имеет
область определения
имеет
область определения
![]() ,
и единственной точкой границы
,
и единственной точкой границы
![]() служит
служит
![]() .
Однако вертикальная прямая
.
Однако вертикальная прямая
![]() не
является вертикальной асимптотой
функции, так как
не
является вертикальной асимптотой
функции, так как
![]() .
.
4). Наклонные и горизонтальные асимптоты.При их поиске, как и при поиске других
асимптотических линий (не обязательно
прямых) полезно выделить более просто,
чем
![]() ,
устроеннуюглавную частьфункции,
то есть такую функцию
,
устроеннуюглавную частьфункции,
то есть такую функцию
![]() ,
что разность
,
что разность
![]() --
бесконечно малая при
--
бесконечно малая при
![]() или
или
![]() .
Тогда график главной части
.
Тогда график главной части
![]() и
есть искомая асимптотическая линия.
Если ясно, что асимптотическая линия
не имеет наклонной либо горизонтальной
асимптоты, то её не имеет и исходный
график
и
есть искомая асимптотическая линия.
Если ясно, что асимптотическая линия
не имеет наклонной либо горизонтальной
асимптоты, то её не имеет и исходный
график
![]() .
Заметим, что все многочлены
.
Заметим, что все многочлены
![]() (при
(при
![]() и
и
![]() )
не имеют асимптотических линий вида
)
не имеют асимптотических линий вида
![]() (докажите
это!). Следовательно, искать в виде
(докажите
это!). Следовательно, искать в виде
![]() прямолинейные
наклонные либо горизонтальные асимптоты
у тех графиков, которые имеют асимптотические
линии в виде графиков многочленов, в
том числе у самих многочленов степени
прямолинейные
наклонные либо горизонтальные асимптоты
у тех графиков, которые имеют асимптотические
линии в виде графиков многочленов, в
том числе у самих многочленов степени
![]() , --
дело бессмысленное: этих прямолинейных
асимптот всё равно нет!
, --
дело бессмысленное: этих прямолинейных
асимптот всё равно нет!
Пример 7.38Рассмотрим функцию
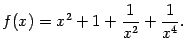 Эта
функция имеет главную часть
Эта
функция имеет главную часть
![]() ,
так как разность
,
так как разность
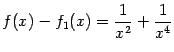 ,
очевидно, стремится к 0 при
,
очевидно, стремится к 0 при
![]() .
Поэтому парабола
.
Поэтому парабола
![]() --
это асимптотическая линия для графика
--
это асимптотическая линия для графика
![]() ;
следовательно, прямолинейных наклонных
и горизонтальных асимптот график этой
функции не имеет.
;
следовательно, прямолинейных наклонных
и горизонтальных асимптот график этой
функции не имеет.
5). Нахождение точки пересечения графика
с осью
![]() состоит
в простом вычислении значения функции
при
состоит
в простом вычислении значения функции
при
![]() .
Нахождение же точек пересечения с осью
.
Нахождение же точек пересечения с осью
![]() может
привести к необходимости решить сложное
алгебраическое уравнение, что, быть
может, удастся сделать лишь приближённо.
О приближённом нахождении корней
уравнений см. ниже, в гл. 9. Отыскав
корни функции
может
привести к необходимости решить сложное
алгебраическое уравнение, что, быть
может, удастся сделать лишь приближённо.
О приближённом нахождении корней
уравнений см. ниже, в гл. 9. Отыскав
корни функции
![]() и
точки разрыва, мы можем определить знак
функции на каждом из интервалов между
этими точками. Это можно сделать либо
вычислив значение функции в какой-нибудь
из точек интервала, либо применив метод
интервалов, знакомый из школьной
программы.
и
точки разрыва, мы можем определить знак
функции на каждом из интервалов между
этими точками. Это можно сделать либо
вычислив значение функции в какой-нибудь
из точек интервала, либо применив метод
интервалов, знакомый из школьной
программы.
6). Нахождение промежутков монотонности.Для этого находят производную
![]() и
решают неравенство
и
решают неравенство
![]() .
На промежутках, где это неравенство
выполнено, функция
.
На промежутках, где это неравенство
выполнено, функция
![]() возрастает.
Там, где выполнено обратное неравенство
возрастает.
Там, где выполнено обратное неравенство
![]() ,
функция
,
функция
![]() убывает.
Если два ннтервала возрастания (или
убывания)
убывает.
Если два ннтервала возрастания (или
убывания)
![]() и
и
![]() примыкают
друг к другу в точке
примыкают
друг к другу в точке
![]() и
функция
и
функция
![]() непрерывна
в этой точке
непрерывна
в этой точке
![]() ,
то
,
то
![]() возрастает
на интервале
возрастает
на интервале
![]() .
.
Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума (пользуясь теоремой 7.10 и не прибегая к теореме 7.11): там, где возрастание сменяется убыванием располагаются локальные максимумы, а там, где убывание сменяется возрастанием -- локальные минимумы.
7). Нахождение интервалов выпуклости
и вогнутостиведётся с помощью второй
производной. Найдя
![]() ,
мы решаем неравенство
,
мы решаем неравенство
![]() .
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство
.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство
![]() ,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута).
,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута).
Заодно определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).
8). Нахождение точек пересечения графика с асимптотой.Этот пункт не носит столь уж обязательного характера, однако нахождение таких точек придаёт исследованию функции и построенному её графику законченность и полноту.
Заметим, что получающиеся в процессе исследования функции точки на осях координат и на графике полезно сразу же наносить на чертёж. Это помогает по ходу дела уяснять вид графика. При этом дальнейшие исследования функции имеют характер уточнений полученного ранее.