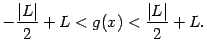- •Функции и их графики Конспекты, лекции, задачи
- •Первый способ задания функции: табличный
- •Clx.Ru - реклама в интернет
- •Упражнения
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Clx.Ru - реклама в интернет
- •Непрерывность функций, точки разрыва Примеры, упражнения Определение непрерывности функции
- •Сводка основных результатов о производных
- •Формула Тейлора теория и практика в примерах Многочлен Тейлора
- •Исследование функций и построение графиков Асимптоты графика функции
- •Достаточные условия локального экстремума
- •Примеры исследования функций и построения графиков
Clx.Ru - реклама в интернет
также является бесконечно малой. Теорема
2.4 утверждает, что тот факт, что разность
![]() бесконечно
мала, означает, что
бесконечно
мала, означает, что
![]() ;
это и требовалось доказать.
;
это и требовалось доказать.
Замечание 2.2В доказанной теоременеутверждается, что если существует
предел суммы, то существуют и пределы
слагаемых. Это неверно, что показывает
простейший пример: пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() и
предел
и
предел
![]() ,
в то время как пределы при
,
в то время как пределы при
![]() функций
функций
![]() и
и
![]() не
существуют.
не
существуют.
Так что из несуществования пределов слагаемых неследует несуществование предела суммы.
Теорема 2.9Пусть функции
![]() и
и
![]() имеют
пределы при одной и той же базе
имеют
пределы при одной и той же базе
![]() :
:
![]()
Тогда функция
![]() также
имеет предел при базе
также
имеет предел при базе
![]() ,
и этот предел
,
и этот предел
![]() равен
произведению пределов сомножителей:
равен
произведению пределов сомножителей:
![]()
Доказательство. Равенство
![]() означает,
в соответствии с теоремой 2.4, что величина
означает,
в соответствии с теоремой 2.4, что величина
![]() --
бесконечно малая; равенство
--
бесконечно малая; равенство
![]() --
что
--
что
![]() --
бесконечно малая. Поэтому
--
бесконечно малая. Поэтому
![]() и
и
![]() ,
откуда
,
откуда
![]()
или
![]()
Покажем, что в правой части этого
равенства стоит бесконечно малая
величина. Величина
![]() --
бесконечно малая согласно следствию
2.3, а величина
--
бесконечно малая согласно следствию
2.3, а величина
![]() --
бесконечно малая по теореме 2.7 (величина
--
бесконечно малая по теореме 2.7 (величина
![]() имеет
предел, равный 0, и, следовательно,
локально ограничена по теореме 2.6).
Поскольку разность между функцией
имеет
предел, равный 0, и, следовательно,
локально ограничена по теореме 2.6).
Поскольку разность между функцией
![]() и
постоянной
и
постоянной
![]() бесконечно
мала при базе
бесконечно
мала при базе
![]() ,
то по теореме 2.4
,
то по теореме 2.4
![]() ;
это и требовалось доказать.
;
это и требовалось доказать.
Замечание 2.3Сделаем замечание,
аналогичное замечанию 2.2: если существует
предел произведения, то отсюда не
следует, что существуют пределы каждого
из сомножителей; доказанная теорема
этого не утверждает. Приведём пример,
который был уже разобран выше: функция
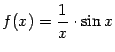 при
при
![]() имеет
предел, равный 0, однако предела
имеет
предел, равный 0, однако предела
![]() при
при
![]() не
существует (хотя другой множитель,
не
существует (хотя другой множитель,
![]() ,
имеет предел при этой базе).
,
имеет предел при этой базе).
Так что из несуществования предела у какого-нибудь сомножителя неследует несуществование предела произведения.
Следствие 2.4Пусть
![]() и
и
![]() (то
есть
(то
есть
![]() --
постоянная величина). Тогда существует
предел функции
--
постоянная величина). Тогда существует
предел функции
![]() ,
равный
,
равный
![]() :
:
![]()
Доказательство. Для доказательства
достаточно заметить, что, согласно
примеру 2.4,
![]() ,
и применить теорему 2.9.
,
и применить теорему 2.9.
Доказанное следствие означает, что
постоянныймножитель
![]() можно
выносить за знак предела, а также вносить
под знак предела. Иными словами, умножение
на постоянную и переход к пределу можно
менять местами.
можно
выносить за знак предела, а также вносить
под знак предела. Иными словами, умножение
на постоянную и переход к пределу можно
менять местами.
Следствие 2.5Пусть функции
![]() имеют
при базе
имеют
при базе
![]() пределы,
равные соответственно
пределы,
равные соответственно
![]() ,
и
,
и
![]() --
постоянные. Тогда
--
постоянные. Тогда
![]()
Доказательство. Оно состоит в
последовательном
![]() -кратном
применении теоремы 2.8 к слагаемым
-кратном
применении теоремы 2.8 к слагаемым
![]() ,
предел которых, согласно предыдущему
следствию, равен
,
предел которых, согласно предыдущему
следствию, равен
![]() .
.
В качестве частного случая можно
рассмотреть предел разности двух
функций. Разность
![]() можно
представить в виде
можно
представить в виде
![]() и
применить следствие 2.5 к этой сумме из
двух слагаемых. Получим тогда, что
и
применить следствие 2.5 к этой сумме из
двух слагаемых. Получим тогда, что
![]()
то есть что разность (как и сумма) сохраняется при переходе к пределу.
Замечание 2.4Утверждение следствия
2.5, с алгебраической точки зрения,
означает, что, во-первых, множество
![]() всех
функций, заданных на фиксированном
окончании
всех
функций, заданных на фиксированном
окончании
![]() базы
базы
![]() и
имеющих предел при базе
и
имеющих предел при базе
![]() --
этолинейное пространство, а
во-вторых-- что операция взятия предела
--
этолинейное пространство, а
во-вторых-- что операция взятия предела
![]() --
этолинейное отображениелинейного
пространства
--
этолинейное отображениелинейного
пространства
![]() в
линейное пространство вещественных
чисел
в
линейное пространство вещественных
чисел
![]() .
Попросту: переход к пределу сохраняет
суммирование и умножение на постоянные.
.
Попросту: переход к пределу сохраняет
суммирование и умножение на постоянные.
Предел отношения двух функций
![]() ,
в отличие от суммы, разности и произведения,
не обязательно равен отношению пределов
числителя
,
в отличие от суммы, разности и произведения,
не обязательно равен отношению пределов
числителя
![]() и
знаменателя
и
знаменателя
![]() ,
даже если пределы
,
даже если пределы
![]() и
и
![]() существуют.
Дело в том, что предел знаменателя может
равняться нулю, и отношение пределов
тогда не имеет смысла, в то время как
предел отношения
существуют.
Дело в том, что предел знаменателя может
равняться нулю, и отношение пределов
тогда не имеет смысла, в то время как
предел отношения
 при
этом вполне может существовать. Приведём
такой простейший пример:
при
этом вполне может существовать. Приведём
такой простейший пример:
Пример 2.15Пусть
![]() ,
,
![]() и
взята база
и
взята база
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() ,
,
![]() и
отношение пределов
и
отношение пределов
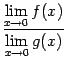 не
имеет смысла. При этом
не
имеет смысла. При этом
 при
при
![]() и
предел отношения существует:
и
предел отношения существует:
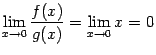 .
.
Оказывается, условия
![]() ,
которое обеспечивает то, что отношение
пределов имеет смысл,-- этого условия
достаточно для того, чтобы предел
отношения двух функций был равен
отношению их пределов. Ниже мы докажем
соответствующую теорему, а пока докажем
такое вспомогательное утверждение.
,
которое обеспечивает то, что отношение
пределов имеет смысл,-- этого условия
достаточно для того, чтобы предел
отношения двух функций был равен
отношению их пределов. Ниже мы докажем
соответствующую теорему, а пока докажем
такое вспомогательное утверждение.
Лемма 2.1Пусть при некоторой базе
![]() существует
предел
существует
предел
![]() .
Тогда функция
.
Тогда функция
 определена
на некотором окончании этой базы и
локально ограничена при этой базе.
определена
на некотором окончании этой базы и
локально ограничена при этой базе.
Доказательство. Возьмём положительное
число
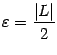 .
По определению предела, в базе
.
По определению предела, в базе
![]() найдётся
такое окончание
найдётся
такое окончание
![]() ,
что при всех
,
что при всех
![]() будет
будет
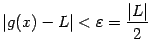 .
Это неравенство можно привести к виду
.
Это неравенство можно привести к виду
|
|
(2.2) |
При
![]() это
неравенство означает, что
это
неравенство означает, что
 ;
так как
;
так как
![]() ,
то и
,
то и
![]() при
всех
при
всех
![]() и,
следовательно, функция
и,
следовательно, функция
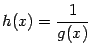 определена
во всех точках окончания
определена
во всех точках окончания
![]() и
удовлетворяет неравенству
и
удовлетворяет неравенству