Функции и их графики Конспекты, лекции, задачи

Основные обозначения и определения

Всюду в тексте учебника мы будем использовать общепринятые обозначения, те, что используются и в школьных учебниках. В частности, означает числовую прямую (множество всех вещественных чисел);означает множество натуральных чисел ;означает множество всех целых чисел ;означаетпустое множество; по определению, в нём нет ни одного элемента;, , и , где , , соответственно,-- замкнутые, полуоткрытые и открытые промежутки: квадратная скобка означает, что соответствующий конец промежутка включается в множество, а круглая скобка-- что не включается;, , и , где , -- замкнутые и открытые лучи (бесконечные промежутки);-- числовая прямая, то же, что и ;-- пересечение (общая часть) множеств и ;-- объединение множеств и (все точки из и все точки из );-- множество тех элементов из , которые не принадлежат ;-- включение в (-- это часть );-- принадлежность элемента множеству (принадлежит );-- элемент непринадлежит множеству ;-- множество, состоящее из элементов ; в частности, -- множество из одного элемента ;-- множество всех тех элементов из , для которых выполняется свойство .

CLX.ru - реклама в интернет

Определение 1.1Пусть и -- два произвольных множества.Функцией из в называется соответствие между элементами множества и множества , при которомкаждомуэлементу сопоставляетсякакой-либо одинэлемент . При этом называетсязначением функции на элементе , что записывается как или . Тот факт, что функция переводит элементы в элементы , записывается так: . Множество называетсяобластью определенияфункции и обозначается .

Рис.1.1.Множество отображается функцией в множество

Пример 1.1Пусть в группе 20 студентов. Рассмотрим множество номеров и множество -- множество фамилий, записанных русским алфавитом. Тогда соответствие , сопоставляющее каждому из номеров студентов в списке группы фамилию этого студента,-- это функция , где -- номер студента в группе (от 1 до 20) и -- фамилия этого студента. Поскольку фамилию имеет каждый студент, значение определено для всех . Очевидно, однако, что далеко не все элементы множества -- множества всевозможных фамилий-- присутствуют в списке группы. Например, если в группе нет студента по фамилииИванов, то элементИвановне будет значением ни при каком . Если же в группе есть однофамильцы по фамилииПетров, то при разных номерах и элементПетровбудет значением функции , то есть и .

На этом примере видно, что, во-первых, множество значений функции

не обязано совпадать со всеммножеством , а может оказаться лишь его частью. Во-вторых, могут найтись такие , что , но . В таком случае часто говорят, что элементы и склеиваютсяпри отображении .

Определение 1.2Если , то есть для любого элемента найдётся элемент такой, что , то функция называетсяотображением на (напомним, что в общем случае -- это отображениеиз в ). Отображение "на" также называютсюръективным отображениемилисюръекцией.

Если для любых двух разных элементов ( ) значения тоже разные ( ), то отображение называетсявложениеммножества в множество , илиинъективным отображением(инъекцией).

Пример 1.2Пусть и отображение для задано формулой . Тогда -- сюръекция, так как любое число из отрезка равно значению при некотором .

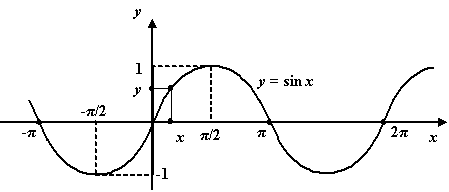
Рис.1.2.Все числа -- это значения функции

Пример 1.3Пусть и отображение задано при формулой . Тогда отображение одновременно является и сюръекцией, и инъекцией, так как 1)любоезначение есть значение при некотором (а именно, при ); 2) никакие дваразныхзначения не могут датьодинаковыхзначений , так как из неравенства следует неравенство .

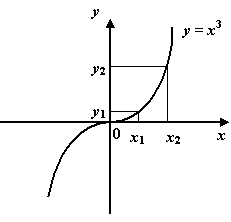
Рис.1.3.Кубы разных чисел не совпадают

CLX.ru - реклама в интернет

Определение 1.3Отображение , которое одновременно является и сюръекцией, и инъекцией, называетсявзаимно-однозначным соответствиеммежду и , илибиекцией. Это означает, что каждому элементу сопоставляется ровно один элемент , причём для каждого элемента имеется такой элемент , который сопоставлен этому .

Замечание 1.1Если отображение -- вложение, то мы можем рассмотреть соответствие, которое устанавливает эта функция между элементами множества и множеством значений функции , то есть частью множества . Пусть . Тогда функция устанавливает взаимно-однозначное соответствие между множествами и . (Более формально: функция , совпадающая с при всех ,-- это биекция. В таких ситуациях, когда функции и имеют одну и ту же область определения и их значения совпадают при всех , мы в дальнейшем будем их обозначать одинаково, в данном случае-- буквой .)

Рис.1.4.Множество взаимно-однозначно отображается на множество

Пример 1.4При сдаче пальто в гардероб каждому сданному пальто соответствует ровно один выданный номерок . Таким образом, между множеством сданных пальто и множествомвыданныхномерков (-- это подмножество множества всехномерков в гардеробе) устанавливается биекция (, ).

Определение 1.4Если -- биекция, то отображение, сопоставляющее каждому тот элемент , который переходит в этот самый при отображении , называетсяобратным отображением(илиобратной функцией) к отображению и обозначается . Таким образом, , и тогда и только тогда, когда (, ).

Пример 1.5В условиях примера 1.4 отображение -- биекция. При выдаче пальто из гардероба по каждому извыданныхномерков находят соответствующее номерку пальто . Соответствие , (, )-- это обратная функция к функции , , то есть .

Очевидно, что в случае, если -- биекция и -- обратная к функция, то для всех и для всех . Последнее равенство показывает, что и что функции и взаимно обратны. (То есть если -- функция, обратная к , то -- функция, обратная к .)

Рис.1.5.Функции и взаимно обратны

Итак, для того чтобы функция имела обратную функцию , функция должна быть биекцией, то есть устанавливать взаимно-однозначное соответствие между и . Тогда обратная функция устанавливает взаимно-однозначное соответствие между и .

Пример 1.6Функция , заданная формулой ,-- это биекция. Обратная к ней функция-- это квадратный корень: .

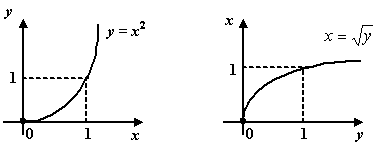
Рис.1.6.Функции и -- взаимно обратны

В математическом анализе основную роль играют такие функции , у которых значениями служат вещественные числа, то есть . Такие функции называютсячисловыми. Функции примеров 1.2, 1.3, 1.6-- числовые. Функции примеров 1.1, 1.4 числовыми не являются.

А вот пример числовой функции, область определения которой, в отличие от предыдущих примеров числовых функций, не лежит на числовой прямой.

Пример 1.7Пусть -- множество всевозможных отрезков , расположенных в (трёхмерном) пространстве, концы которых (точки и ) не совпадают. Пусть соответствие сопоставляет каждому такому отрезку его длину . Так как длина отрезка-- число, то -- числовая функция, . Легко видеть, что область её значений состоит из всех положительных чисел: .

Замечание 1.2В первых главах учебника мы ограничимся в основном такими числовыми функциями , область определения которых также является подмножеством числовой прямой , то есть такими функциями , где и . Такие функции называютсячисловыми функциями одного переменного. В дальнейшем (во втором семестре) мы будем также изучать функции, зависящие от нескольких вещественных переменных, то есть функции, область определения которых-- подмножество в пространстве , равном прямому произведению экземпляров множества (определение прямого произведения нескольких множеств мы дадим ниже).

Определение 1.5Графиком функции называется множество пар элементов и , такое, что в каждой паре второй элемент -- это значение функции , соответствующее первому элементу пары, то есть .

Рассмотрим множество всевозможныхпар , где , . Это множество всевозможных пар называетсяпрямым произведениеммножества на множество и обозначается .

Ясно, что график функции -- это подмножество прямого произведения :

В некоторых из рассмотренных выше примеров функций были приведены на рисунках графики этих функций. График примера 1.2-- подмножество в ; график примера 1.3-- подмножество в ; оба графика примера 1.6-- подмножества в (здесь мы ввели обозначение , которого будем придерживаться и далее).

Пример 1.8Пусть -- круг радиуса 1 (включая окружность радиуса 1-- границу круга) на числовой плоскости с координатами и , с центром в точке . Функцию в любой точке круга зададим как расстояние от этой точки до центра. Таким образом, , где .

Графиком этой функции является подмножество прямого произведения . Это прямое произведение-- бесконечный цилиндр с круговым сечением, находящийся в пространстве . Обозначим координаты точек в через . Тогда графику принадлежат те точки, для которых выполнены соотношения и .

Множество представляет собой кусок конической поверхности с вершиной в точке , с высотой 1 и радиусом основания 1.

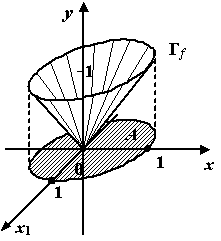
Рис.1.7.График расстояния до точки -- это конус

Как мы видим, в случае, когда -- подмножество плоскости , график числовой функции -- это подмножество точек пространства . Если же -- подмножество точек пространства , то графиком числовой функции будет подмножество четырёхмерного пространства, точнее, его подмножества . В связи с этим,изобразитьграфик такой функции на чертеже не представляется возможным, хотя, конечно, можно постараться как-то этот график описать каким-то иным способом.

Пример 1.9Пусть и для каждой точки значение функции в этой точке-- это квадрат расстояния от до точки , то есть . Тогда график -- это подмножество в :

Изобразить этот график, то есть нарисовать трёхмерную поверхность, расположенную в четырёхмерном пространстве, мы уже не в состоянии, однако формула позволяет изучать этот график. Например, можно заметить, что двумерное сечение этого графика плоскостью -- это парабола в плоскости , а сечение трёхмерным пространством -- это одна точка .

Наибольший интерес с точки зрения наглядности представляют графики числовых функций одного переменного. Изучению поведения таких функций и построению их графиков будет уделено основное внимание в следующих главах.

Как мы видим из приведённых выше примеров, способы эти могут быть самые разные, от словесно-описательного в примерах 1.1, 1.4 до задания функции формулой вида в примерах 1.2, 1.3, 1.6, 1.8, 1.9. Способ задания функции зависит от того, какова природа множеств и и как по заданному определяется . Выделим основные из этих способов.