3.2. Факторы, влияющие на интенсивность линий

Относительная интенсивность линии на рентгенограмме I/I₀ задается следующим соотношением:

(3.1)

где I₀  интенсивность первичного пучка, p  множитель повторяемости, |F|²  структурный фактор с учетом тепловых колебаний атомов, А - абсорбционный множитель интенсивности. Рассмотрим составляющие этой формулы.

1. Величины К зависят от способа съемки рентгенограммы. При съемке на прохождение (фотометоды, цилиндрические образцы):

(3.2)

при съемке на отражение (дифрактометрия, поликристаллический шлиф или иной плоский образец):

(3.3)

где e и m  заряд и масса электрона, c - скорость света,  -длина волны рентгеновского излучения, N - число элементарных ячеек в единице объема, R - радиус камеры или окружности, по которой движется счетчик в дифрактометре, l - ширина полосы почернения или высота щели счетчика, V-облучаемый объем образца и  - линейный коэффициент поглощения (берется для монокристалла).

2. Параметр в уравнении 3.1 учитывает поляризацию рентгеновского излучения при отражении от кристалла и другие факторы, определяющие угловую зависимость интенсивности для различных геометрий получения рентгенограмм.

3. Абсорбционный множитель А учитывает поглощение излучения образцом. Если цилиндрический образец снимается в рентгеновских камерах, то А зависит от r (  линейный коэффициент поглощения, r - радиус образца) и увеличивается с углом . Наибольшее влияние на интенсивность линий поглощения оказывает при небольших углах отражения. В случае съемки на дифрактометре поглощение постоянно для всех углов скольжения. В то же время с учетом всех факторов, влияющих на поглощение, установлено, что при сильном поглощении относительная интенсивность линий, полученных в рентгеновских камерах, с увеличением  почти не меняется. Напротив, при съемке на дифрактометре  интенсивность резко уменьшается при росте  от 0 до 45°.

4. Структурный фактор |F|²  квадрат амплитуды волны, рассеянной элементарной ячейкой в направлении, определяемом индексами hkl, зависит от расположения атомов в этой ячейке, т.е.  от структуры кристалла. Структурный фактор |F_hkl|² равен произведению структурной амплитуды F_hkl на комплексно сопряженную величину F*_hkl. Структурная амплитуда F_hkl зависит от координат атомов, их атомных амплитуд и индексов плоскости:

(3.4)

(3.5)

Суммирование ведется по всем атомам i в пределах одной элементарной ячейки. Иначе эту зависимость можно записать

(3.6)

где

(3.7)

(3.8)

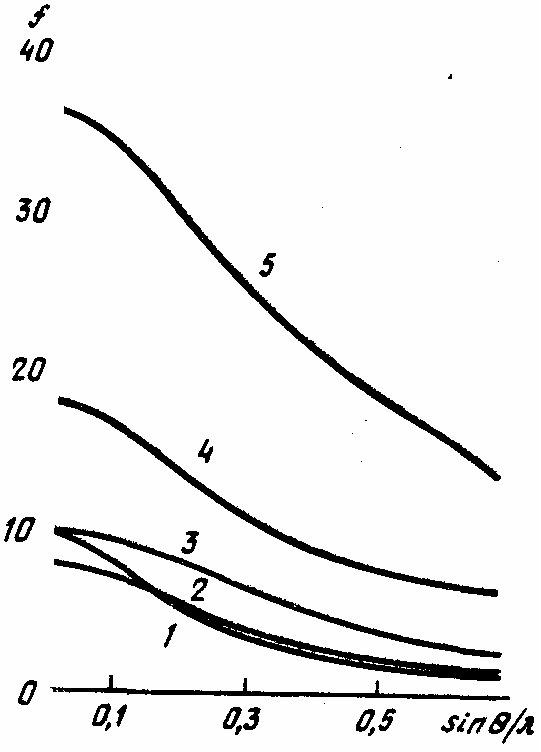
Атомные амплитуды рассеяния f_i являются функцией sin /. При sin/ = 0 f_i равны сумме амплитуд рассеяния каждым электроном атомов. К примеру, на рис. 14 показаны эти зависимости для атома кислорода и нескольких ионов.

Как видно из рис. 14, изменение f_i с ростом sin / для атомов с небольшими атомными номерами является относительно более резким, чем для тяжелых атомов с более компактным распределением электронной плотности вблизи ядра. Поэтому расположение легких атомов в структуре влияет на интенсивность только при сравнительно небольших sin /. Кривые атомного рассеяния для разноименно заряженных ионов с одинаковым числом электронов (например, Na⁺ и O^2), отражают разную зависимость f_i от угла рассеяния: для отрицательно заряженных ионов с более диффузным распределением электронной плотности уменьшение f_i с ростом sin / является более значительным.

Анализом структурных амплитуд для разных пространственных групп получены так называемые правила систематических погасаний, т.е. найдены комбинации индексов, которым отвечает нулевое значение F_hkl а значит, и I_hkl.

5. В интенсивность рассеяния вносит вклад, так называемые «тепловые колебания атомов». Тепловые колебания приводят к уменьшению когерентности рассеяния, как бы к «размазыванию» электронной плотности рассеивающего атома и дают примерно такой же эффект, как уменьшение эффективного заряда при том же числе электронов (сравните f_i для O^2 и Na⁺).

Влияние тепловых колебаний учитывается множителем Дебая-Уоллера: вместо f_i берется f_ie^2M. В простейшем случае:

, (3.9)

Рис. 14. Зависимость структурных амплитуд от sin / для атома кислорода О (1) и следующих ионов O2- (2), Na+ (3), K+ (4), Rb+ (5).

где В – фактор Дебая – Уоллера, определяемый среднеквадратичной амплитудой тепловых колебаний атомов <u²>:

В = <u²>/2 , и <u²> = <r²>  <r>², (3.10)

где r – межъядерное расстояние; символ <…> означает усреднение по величине межъядерного расстояния r при данной температуре T.

Для кристаллов с большой концентрацией вакансий или статистическим заполнением одной позиции атомами разного сорта значения В_i, получаемые при обработке экспериментальных данных, являются эффективным параметром, учитывающим не только тепловые колебания, но и изменение f_i из-за изменения заселенности структурных позиций.

Таким образом, интенсивность линий на рентгенограммах прямо зависит от:

• способа получения рентгенограмм;

• типа используемых образцов;

• рассеивающей способности атомов, составляющих отражающие плоскости;

• cимметрии и структуры кристаллов, определяющих также и правила систематических погасаний;

• искажения решетки искомой фазы за счет существования в поликристаллических образцах дефектов разного рода.