1.1. Симметрия и ее элементы

Благодаря правильной, периодически повторяющейся картине расположения атомов в кристалле он обладает определенным набором элементов симметрии. Симметрией называется свойство бесконечного пространства или его конечной области (фигуры, тела) совмещаться с самим собой после выполнения некоторых преобразований или операций S, называемых операциями симметрии [2,3].

Симметрия представляет собой обобщение понятия равенства. Равными называются два тела, у которых равны расстояния между соответственными точками:

r₁₂ = r'₁₂ (1.3)

Условию (1.3) удовлетворяют два равных тела, различающихся положением в пространстве. Например, две одинаковые правые перчатки, которые можно совместить друг с другом параллельным переносом вдоль некоторой прямой и поворотом вокруг этой прямой (винтовым движением). В частных случаях такое совмещение может быть выполнено одним из преобразований: либо параллельным переносом, либо поворотом вокруг оси. Таким образом, движение тела без деформации представляет собой одно из симметричных преобразований. Условию (1.3) удовлетворяют, например, два тела, которые совмещаются друг с другом после отражения в зеркале (рис.3). Зеркально-симметричными являются правая и левая система координат.

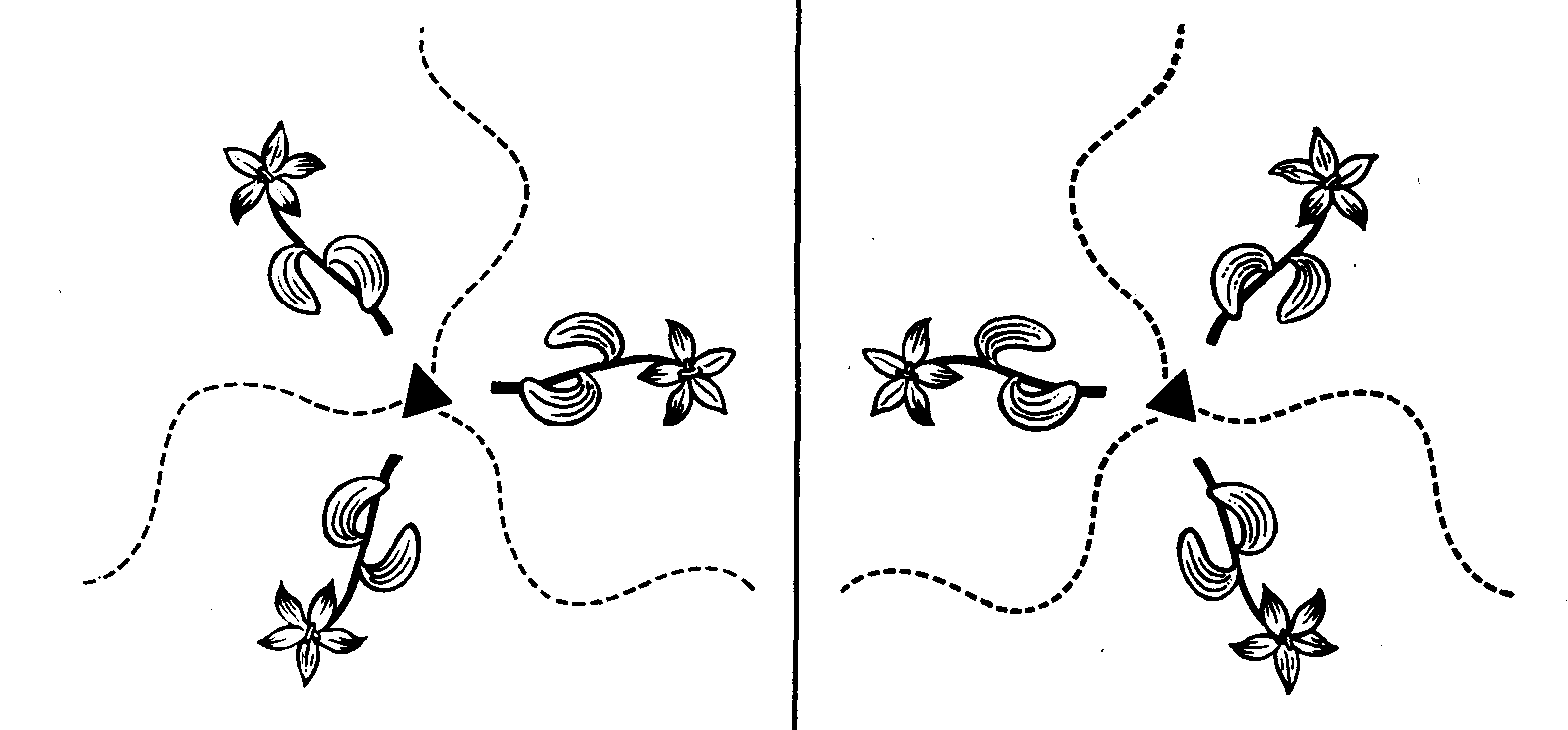
а	б
Рис. 3. Операция симметрии – зеркальное отражение. Показано на примере правой и левой перчаток (а) и цветков (б), расположенных на оси симметрии третьего порядка – эта ось обозначена треугольником и располагается перпендикулярно рисунку

К преобразованиям симметрии S относятся такие преобразования координат, при которых сохраняется инвариантность расстояний между двумя произвольно выбранными точками тела:

r' = S( r ) = r, (1.4)

Если после выполнения этих преобразований происходит совмещение тела с самим собой, то преобразования (1.4) принадлежат к группе линейных преобразований. Связь между координатами x'_i и x_j задается матрицей с постоянными коэффициентами вида:

x₁ x₂ x₃

x'₁ a₁₁ a₁₂ a₁₃

x'₂ a₂₁ a₂₂ a₂₃

x'₃ a₃₁ a₃₂ a₃₃ (1.5)

Преобразования (1.5) в общем случае описывают однородные деформации, при которых прямые и плоскости преобразуются соответственно в прямые и плоскости. Требование (1.5) означает, что преобразования координат должны быть ортогональными и не изменяющими ни углов между прямыми, ни масштаба:

r'² = r² (1.6)

Например, ортогональная система координат остаётся ортогональной, а условие ортогональности имеет вид:

a_ik² = 1, (1.7)

где a_ik – детерминант, составленный из коэффициентов матрицы (1.5). Из условия ортогональности (1.7) получаем:

a_ik =  1 (1.8)

Знак (+) означает, что преобразование не меняет типа системы координат, а знак () – что преобразование меняет тип системы координат – правая система переходит при этом в левую и наоборот (см. например, рис.3).

Первичным преобразованием симметрии является отражение в плоскости. Это симметричное преобразование, состоящее из двух элементарных операций отражений. При неограниченном числе отражений точки 1 и 2 преобразуются друг в друга. Порядок или кратность операции отражения в плоскости равны двум.

Пусть m является координатной плоскостью (X₂X₃), а ось X₁ направлена по нормали к плоскости m. Тогда координаты группы двух симметрически эквивалентных точек, преобразующихся друг в друга отражением в координатной плоскости (X₂X₃), будут:

(x₁, x₂, x₃) и (-x₁, x₂, x₃). (1.9)

Отражение в центре симметрии – инверсия (i) является более сложным преобразованием по сравнению с отражением в плоскости. Его можно представить как результат отражений в трех взаимно перпендикулярных плоскостях. При отражении точки 1 в каждой из этих плоскостей изменяется знак у соответствующей координаты. Поэтому координаты симметрически эквивалентной точки 2, получаемой путем инверсии в начале координат, равны координатам точки 1 с измененными знаками:

(x₁, x₂, x₃) и (x₁, x₂, x₃), (1.10)

или, в векторной форме,

r₂ = r₁, (1.11)

откуда видно, что отражения в трех ортогональных плоскостях эквивалентны инверсии в точке пересечения этих плоскостей, являющейся центром симметрии. Отражениям в двух плоскостях эквивалентен поворот вокруг оси и трансляция.

Преобразования симметрии, не изменяющие тип системы координат, называют преобразованиями I рода, а изменяющие тип системы координат  преобразованиями II рода. Движения тела – повороты и параллельные переносы – примеры преобразований симметрии I рода. Отражение в зеркальной плоскости и инверсия в центре симметрии – примеры преобразований симметрии II рода. Четное число преобразований симметрии II рода представляет собой преобразования симметрии I рода. Нечетное число преобразований симметрии II рода представляет собой преобразования симметрии II рода.

Плоскость отражения, ось поворота, центр инверсии, вектор переноса (трансляция) – это геометрические образы, с помощью которых можно осуществить соответствующие преобразования симметрии. Эти образы называют элементами симметрии.

Приведем обозначения некоторых из элементов симметрии с конечной кратностью:

P или m – плоскость симметрии;

C_n или n  ось симметрии;

S_n – зеркально-поворотная ось симметрии, сочетающая поворот вокруг оси n с отражением в перпендикулярной к ней плоскости m;

n – инверсионная ось симметрии, сочетающая поворот вокруг оси n с инверсией в центре симметрии i, лежащем на оси поворота.