1.3. Пространственные группы

Полная симметрия кристаллической решетки, т. е. симметрия расположения составляющих ее атомов, определяется, как отмечалось, сочетанием трансляционной симметрии и элементов симметрии, связанных с поворотами и отражениями. Совокупность элементов симметрии, присущих данной кристаллической решетке, называется пространственной группой этой решетки.

Для определения пространственной группы кристаллической решетки нужно, очевидно, указать ее решетку Браве и те элементы симметрии, которые связаны с поворотами и отражениями, т.е. расположение плоскостей и осей симметрии. Любая пространственная группа может быть отнесена к одному из 32 кристаллических классов

Знаменитым кристаллографом Е. С. Федоровым было показано, что всего возможно 230 различных пространственных групп, которые и распределяются по указанным кристаллическим классам (Федоровские группы).

1.4. Символические обозначения плоскостей и направлений в кристалле. Индексы Миллера

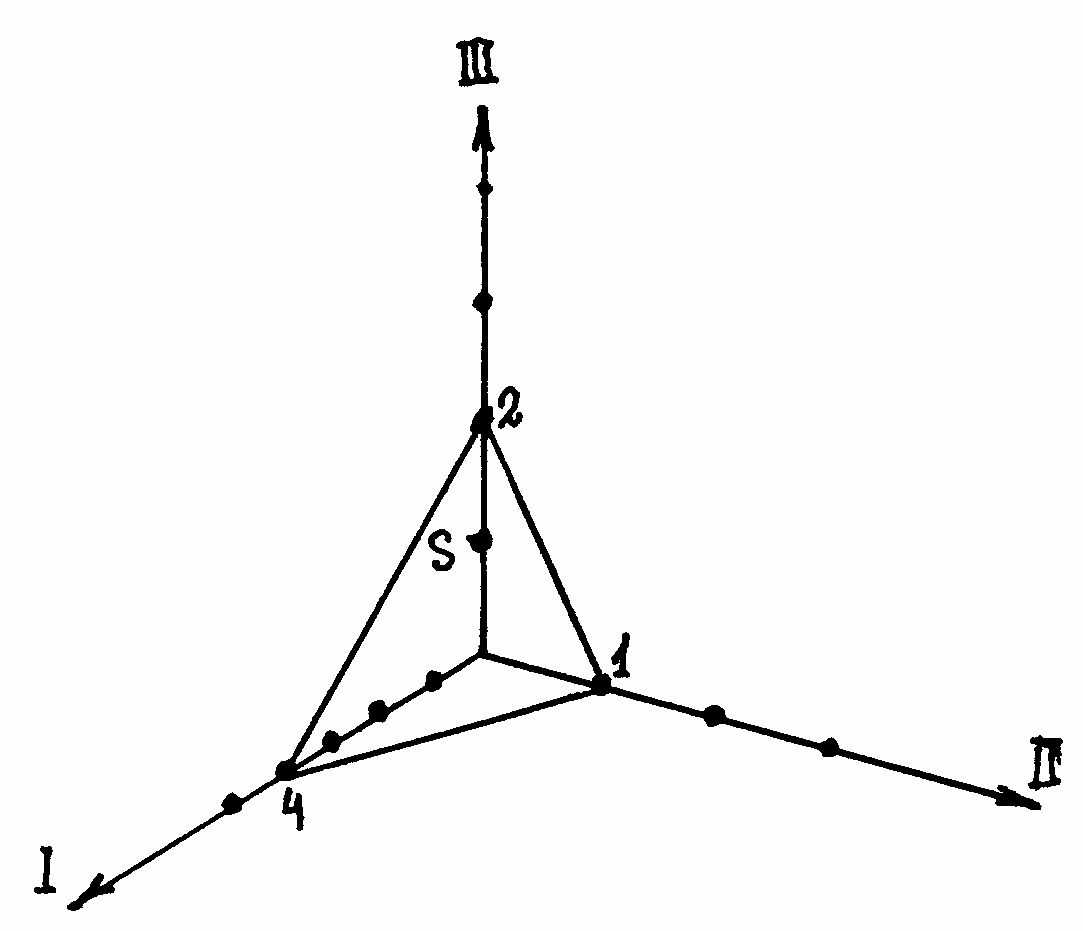
Рис.6. Координатные оси и плоскости

Анизотропия кристалла делает необходимым выделение и соответствующее обозначение различных плоскостей (граней) и направлений (например, ребер) в кристалле. Для этого пользуются специальной системой координат, связанной с кристаллом так, что координатные оси обычно проводятся параллельно осям симметрии или перпендикулярно к плоскостям симметрии, а начало координат совпадает с одним из узлов решетки.

Координаты в такой системе измеряются в единицах, равных постоянным (параметрам) решетки. Положение какой-либо плоскости однозначно определяется координатами любых трех точек этой плоскости, например тех, в которых она пересекается тремя осями координат.

Пусть оси I, II и III являются координатными осями (рис.6) и нужно описать плоскость S. Если, например, плоскость пересекает ось I в точке на расстоянии в 4 единицы в направлении оси I, ось II на расстоянии в 1 единицу и ось III на расстоянии в две единицы, то положение плоскости задается тройкой чисел: 4, 1 и 2.

Однако для обозначения плоскостей в кристалле принято пользоваться не этими числами, а так называемыми индексами Миллера, которые определяются так: находим координаты трех точек пересечения плоскости с координатными осями (в единицах постоянных решетки). Обратные значения полученных чисел приводим к одному знаменателю и знаменатель отбрасываем. Числители дробей и дают индексы Миллера.

Например, для только что рассмотренной плоскости, пересекающей оси координат в точках 4, 1 и 2, обратные величины координат будут, соответственно 1/4, 1 и 1/2, общий знаменатель этих дробей равен 4 и индексы Миллера окажутся, таким образом, равными 1, 4 и 2. Эти числа заключаются в круглые скобки, так что интересующая нас плоскость символически обозначается (142) (читается «один, четыре, два»).

Данный набор индексов определяет, очевидно, не одну плоскость, а все семейство параллельных плоскостей. Индексы Миллера обозначаются буквами h, k, l. Если плоскость параллельна одной из осей координат, т. е. пересекает ее в бесконечности, то соответствующий индекс равен нулю.

(100)	(110)	(111)
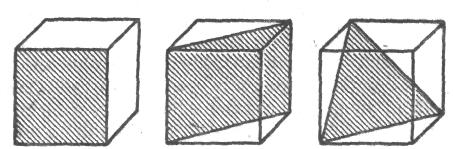
Рис. 7. Кубическая решетка. Вид секущих плоскостей разного типа.

На рис. 7 показаны сечения некоторыми плоскостями (с индексами 100; 110, 111) кубической ячейки.

Направления в кристалле также задаются индексами, которые определяются следующим образом: вдоль определяемого направления выбирают некоторый вектор произвольной длины и определяют величины составляющих этого вектора по осям координат в единицах постоянной решетки. Тогда индексами этого направления будут три наименьших целых числа, отношения которых между собой равны отношениям составляющих вектора.

Например, если компоненты вектора равны соответственно 6, 4 и 8 единицам, то индексами соответствующего этому вектору направления будут 3, 2 и 4. Эти числа заключаются в квадратные скобки – [324]. Индексы направлений обозначают буквами u, v и w. Направление, определяемое данным набором индексов [u, v, w], иногда (а для кубического кристалла всегда) оказывается перпендикулярным к плоскости с таким же набором индексов Миллера.