§4. Формула полной вероятности. Формула Байеса

Пусть событие А может произойти только с одним из событий образующих полную систему попарно несовместных событий (рис.1.3). Тогда вероятность события А вычисляется по формуле полной вероятности:

. (1.10)

Д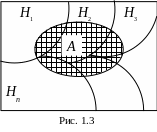 ействительно, так как событие А может произойти только с одним из событий образующих полную систему, то . Из рис.1.3 видно, что попарно несовместны. Поэтому

Применив правило умножения вероятностей к каждому слагаемому равенства , получим формулу (1.10).

В тесной связи с формулой полной вероятности находится так называемая формула Байеса:

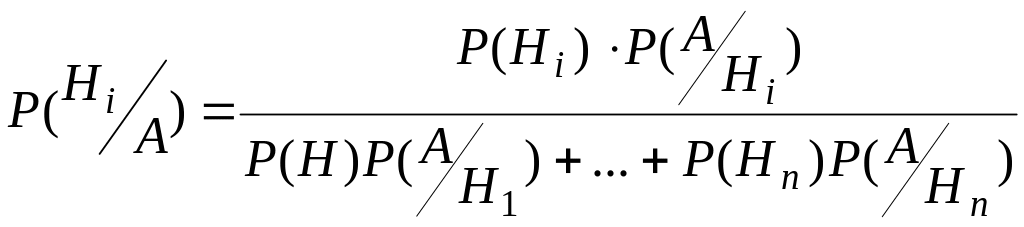, (1.11)

где - вероятность гипотезы после того, как имело место событие А.

Формула Байеса позволяет переоценить вероятность гипотез, принятых до испытания, по результатам уже произведённого испытания.

Задача 1. Слепой старец вышел из пункта А в пункт В. Считая, что в каждом из пунктов А, В, С, Д, Е дорога выбирается наудачу, найти вероятность того, что он дойдёт до пункта В.

Р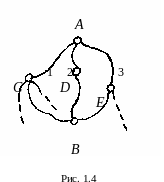 ешение. Пусть А – событие, заключающееся в том, что старец дойдёт до пункта В. В качестве гипотез примем события:

- “старец пошёл по дороге 1”;

- “старец пошёл по дороге 2”;

- “старец пошёл по дороге 3”.

Так как в пункте А дорога выбирается наудачу, то

.

Далее, - вероятность того, что старец дойдёт до В, если он пошёл по дороге 1, равна , так как из пункта С в пункт В ведут три дороги. Аналогично рассуждая, получим .

По формуле (1.10) имеем

Задача 2. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле , при втором – , при третьем – . При одном попадании вероятность поражения цели равна 0,4, при двух 0,7, при трёх 1,0. Найти вероятность поражения цели при трёх выстрелах.

Решение. Обозначим события:

А – “поражение цели при трёх выстрелах”;

– “одно попадание”;

– “два попадания”;

– “три попадания”;

– “ни одного попадания”.

Из условия задачи имеем

, , , .

Если - соответственно вероятности попадания при первом, втором, третьем выстрелах, то 1– , 1– , 1– – соответственно вероятности при тех же выстрелах.

Следовательно,

так как попадание могло произойти либо при первом выстреле, либо при втором, либо при третьем.

Аналогично:

,

т.к. имело место три выстрела и все три попадания.

,

т.к. имело место три выстрела и все три промаха. Очевидно, что

.

Подставим полученные значения в формулу (1.10):

.

Задача 3. (поучительная). Студент идёт на экзамен, зная 10 билетов из 25. В каком случае вероятность вытащить “счастливый” билет больше, если он берёт билет первым или вторым?

Решение. Если студент идёт первым, то вероятность вытащить “счастливый” билет, очевидно, равна .

Предположим теперь, что он берёт билет вторым. Введём гипотезы:

– вошедший первым вытащил “счастливый” (для второго) билет;

– вошедший первым вытащил “несчастливый” (для второго) билет. Тогда

;

Обозначим через А событие “студент, зашедший вторым, вытащил “счастливый” для него билет”. Тогда

.

Так как после того, как первый взял “счастливый” билет, из 24 оставшихся билетов “счастливых” осталось только 9.

Аналогично

.

По формуле (1.10)

.

Таким образом, вероятность вытащить «счастливый» билет не зависит от того, идёт ли студент на экзамен первым или вторым.

Задача 4. Из 16 стрелков 5 попадают в мишень с вероятностью 0,8; 7 – с вероятностью 0,7; 4 – с вероятностью 0,5. Наудачу выбранный стрелок произвёл выстрел, но в мишень не попал. К какой же группе вероятнее всего принадлежит стрелок?

Решение. Здесь на результаты влияют два фактора: с одной стороны, вероятность попадания, с другой – количество стрелков в группе. Например, наибольшие шансы не попасть у стрелков третьей группы, но зато их только четверо.

Пусть событие А – “промах наудачу выбранного стрелка”

“наудачу выбранный стрелок из первой группы”;

 “наудачу выбранный стрелок из второй группы”;

“наудачу выбранный стрелок из третьей группы”.

Тогда:

Вероятнее всего, стрелок принадлежит ко второй группе.

Задача 5. Имеется две партии деталей, причём известно, что в одной партии все детали удовлетворяют техническим условиям, а в другой партии деталей недоброкачественных. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что вторая деталь из этой же партии окажется недоброкачественной, если первая деталь после проверки возвращена в партию.

Решение. Пусть событие А – “первая деталь доброкачественная”.

Гипотезы:

– “взята партия, содержащая недоброкачественные детали”;

– “взята партия доброкачественных деталей”.

По условию задачи:

, , ;

.

После первого испытания вероятность того, что партия содержит недоброкачественные детали, равна:

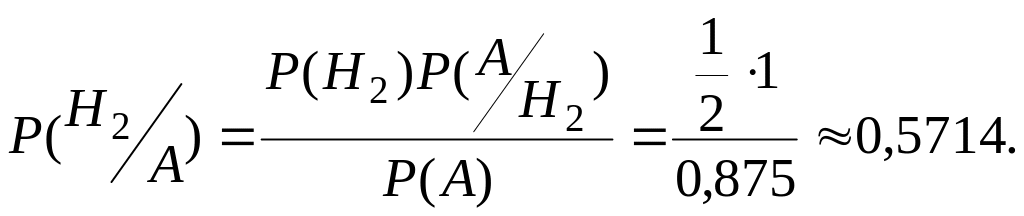
Пусть событие В состоит в том, что при втором испытании деталь оказалась недоброкачественной. Вероятность данного события также находится по формуле полной вероятности. Если и – вероятности гипотез и после испытания, то согласно предыдущим вычислениям

Кроме того, , .

Поэтому искомая вероятность