5. Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых появляется событие А с вероятностью, равной р (0 < р < 1) и, следовательно, не появляется с вероятностью q= 1– р. Как только событие А появилось, испытания прекращаются. Следовательно, если событие А появилось в к-м испытании, то в предшествующих к–1 испытаниях оно не появлялось.

Обозначим через Х дискретную случайную величину – число испытаний, которые произошли до первого появления события А. Очевидно, возможными значениями Х являются натуральные числа: х₁= 1, х₂=2, ....

Пусть в первых к–1 испытаниях событие А не наступило, а в к-м испытании появилось. Вероятность этого сложного события, по теореме умножения вероятностей независимых событий,

P(X=к)=q ^к-1p. (1.54)

Полагая к=l, 2, ... в формуле (1.54), получим геометрическую прогрессию с первым членом р и знаменателем q (0<q<1):

p, qp, q²p,…, q^к-1р,… . (1.55)

Поэтому распределение (1.55) называют геометрическим.

Запишем закон распределения в виде таблицы.

хi	1	2	3	…	к	…
pi	p	qp	q2p	…	qк-1р	…

Легко проверить, что

.

Математическое ожидание и дисперсия случайной величины, имеющей геометрическое распределение, равны.

М(Х)=1/p, а D(X)=q/p². (1.56)

Задача 7. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р = 0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. По условию, р = 0,6; q = 0,4; к = 3. Искомая вероятность по формуле (1.54)

Р(к=3)= 0,4²·0,6 = 0,096.

Задача 8. Снайпер стреляет по замаскированному противнику до первого попадания. Вероятность промаха при отдельном выстреле равна . Найти математическое ожидание числа промахов.

Решение. Возможные значения случайной величины X – числа промахов: 0, 1, 2, ..., к, ...

.

Ряд распределения случайной величины X:

Х	0	1	2	…	к	…
р				…		…

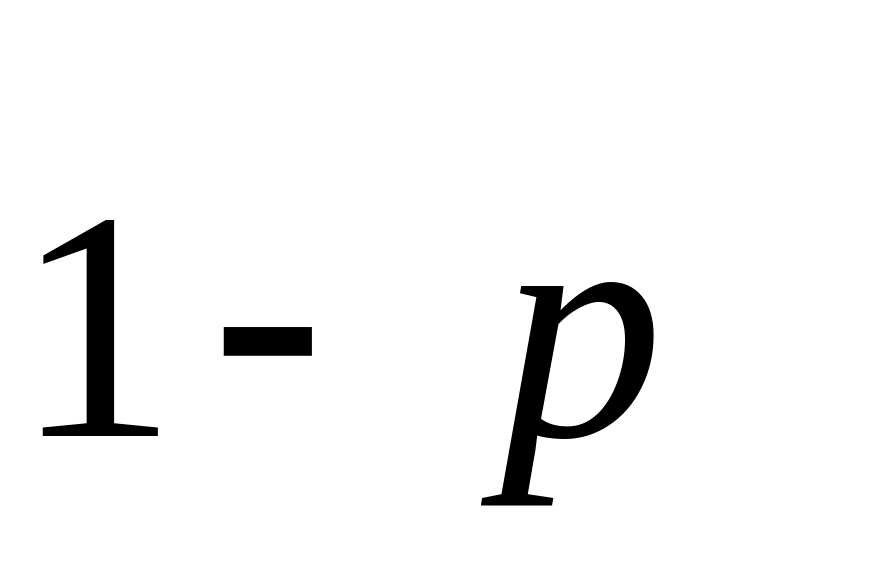
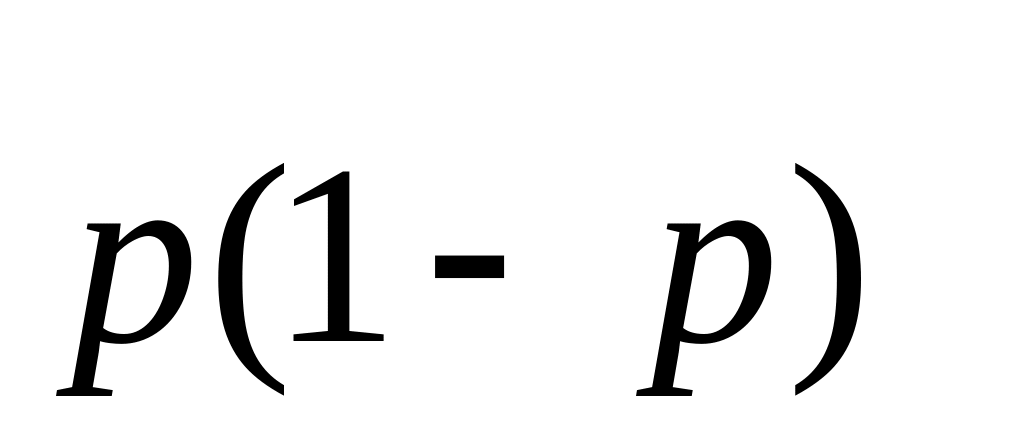
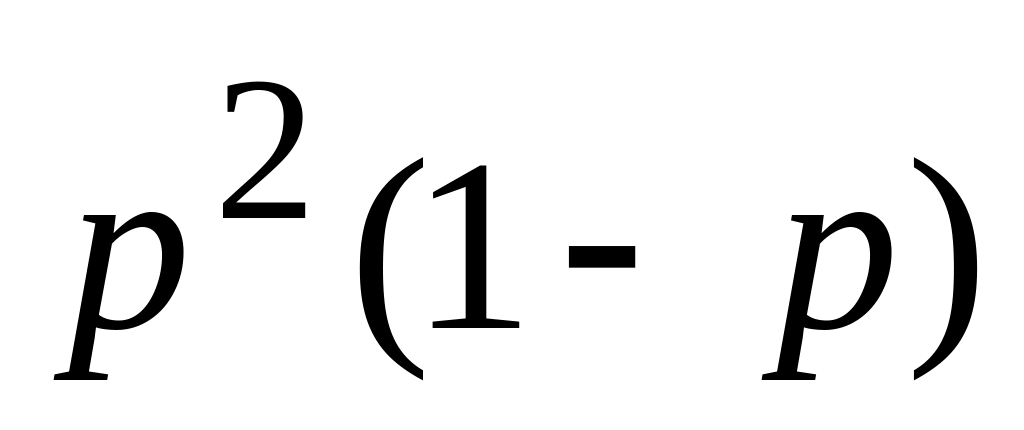
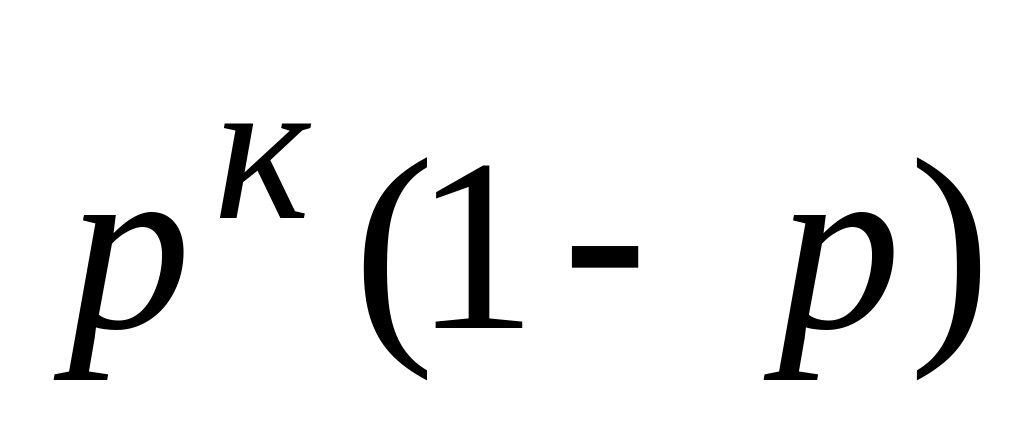
Полученное распределение является геометрическим (см. (1.56)) .

Задачи для самостоятельного решения

7.01. Случайная величина X имеет биноминальный закон распределения с числовыми характеристиками . Определить вероятность попадания случайной величины X на отрезок

7.02. Известно, что в партии деталей имеется 10% бракованных. Найти закон распределения случайной величины X – числа годных деталей из пяти, выбранных наудачу. Определить числовые характеристики и .

7.03. Число атак истребителя, которым может подвергнуться бомбардировщик на территории противника, есть случайная величина, распределённая по закону Пуассона с математическим ожиданием . Каждая атака с вероятностью 0,4 заканчивается поражением бомбардировщика. Определить вероятность поражения бомбардировщика.

7.04. Монету бросают до первого появления герба. Найти среднее число бросаний.

7.05. Цена деления шкалы амперметра равна 0,2 ампера. Показания амперметра определяют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка, превышающая 0,03 ампера.

7.06. Вероятность обнаружения затонувшего судна за время поиска задаётся формулой . Определить математическое ожидание случайной величины Т– времени поиска затонувшего судна.

7.07. Нагрузка на стержень подчиняется нормальному закону распределения с числовыми характеристиками: . Усилие, разрушающее стержень, составляет . Найти вероятность разрушения стержня.

7.08. Станок-автомат изготавливает валики, контролируя их диаметр X. Считая, что X распределено нормально, . Найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготавливаемых валиков.

7.09. Вероятность взятой детали в пределах допуска из большой партии деталей равна: . Найти математическое ожидание и дисперсию числа деталей в пределах допуска из 8 деталей, взятых наудачу.

7.10. Поезд данного маршрута городского трамвая ждут с интервалом 5 минут. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через минуту после ухода предыдущего поезда, но не позднее чем за две минуты до отхода следующего поезда?

7.11. Случайная величина X распределена по нормальному закону с математическим ожиданием и дисперсией . Вычислить вероятность попадания случайной величины в интервал .

7.12. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределённой по нормальному закону. Если стандартная длина равна 40 см и среднее квадратическое отклонение равно 0,4 см, то какую точность длины изделия можно гарантировать с вероятностью 0,8?

7.13. Число частиц, излученных радиоактивным элементом в течение произвольного промежутка времени, имеет распределение Пуассона с параметром . Найти вероятность того, что число частиц, излученных за две секунды, будет заключено в отрезке .

7.14. Дистанция X между двумя соседними самолётами в строю имеет показательное распределение с м. Опасность столкновения самолётов может возникнуть при уменьшении дистанции до 20 м. Найти вероятность того, что возникает опасность столкновения самолётов в воздухе.

7.15. Все значения равномерно распределённой случайной величины лежат на отрезке . Найти вероятность попадания случайной величины в промежуток .

7.16. Книга в 1000 страниц имеет 100 опечаток. Какова вероятность того, что на случайно выбранной странице не менее четырёх опечаток?

7.17. Автоматическая телефонная станция получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит 2 вызова?

7.18. Среди семян ржи имеется 0,4% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

7.19. Для какого значения К функция

является функцией плотности распределения?

7.20. Непрерывная случайная величина Х распределена по показательному закону:

Найти вероятность того, что в результате испытаний Х попадёт в интервал (0,2; 0,5).

7.21. Случайная величина Х распределена по нормальному закону с математическим ожиданием М(Х) = 40 и дисперсией D(Х) = 200. Вычислить вероятность попадания случайной величины в интервал (30; 80).

7.22. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределённая по нормальному закону, с математическим ожиданием а = 65 т и средним квадратичным отклонением σ =0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

7.23. Диаметр детали, изготовленной на станке, случайная величина, распределённая по нормальному закону с математическим ожиданием а = 25 см и средним квадратичным отклонением σ = 0,4 см. Найти вероятность того, что две взятые наудачу детали имеют отклонение от математического ожидания по абсолютной величине не более 0,16 см.

7.24. Диаметр выпускаемой детали – случайная величина, подчинённая нормальному закону с математическим ожиданием 5 см и средним квадратичным отклонением 0,9 см. Установить, в каких границах следует ожидать размер диаметра детали, чтобы вероятность не выйти за эти границы была равна 0,95.

7.25. Вероятность безотказной работы телевизора распределена по показательному закону: . Найти вероятность того, что телевизор проработал 1000 часов.