§7. Важнейшие примеры распределений

В настоящем параграфе приводятся наиболее часто встречающиеся типы распределений непрерывных и дискретных случайных величин и примеры их применения.

1. Биноминальное распределение

Рассмотрим серию из п независимых испытаний, в каждом из которых вероятность наступления события А равна р. Случайная величина Х означает число наступлений событий. Она дискретна, и ее возможными значениями являются неотрицательные целые числа 0, 1, 2, ... , п.

Закон распределения случайной величины Х задается уже известной нам формулой (см. § 5 )

, (1.29)

определяющей вероятность равенства Х= к. Как было указано в § 5, это выражение представляет член разложения бинома (р +q)ⁿ. Поэтому говорят, что случайная величина Х подчиняется биномиальному закону распределения. Примеры приложений биномиального распределения уже встречались нам в предыдущих параграфах.

Чтобы вычислить дисперсию случайной величины, распределенной по биномиальному закону, воспользуемся теоремой о дисперсии суммы случайных величин. Пусть случайная величина Х означает количество наступлений события А в серии из п испытаний, причем в каждом испытании вероятность наступления события равна р. Положим

X=X₁+ X₂+…+ X_n,

где X_i – случайная величина, принимающая только два значения: 1, если в i-м испытании событие А произошло, и 0, если оно не произошло. Закон распределения каждой из величин X_i одинаков и задается таблицей

xi	0	1
pi	q =1-p	р

Математическое ожидание X_i равно

M(X_i)=0·q+1·p=p.

Отсюда, пользуясь теоремой о математическом ожидании суммы, сразу видим, что

М(Х)= пр. (1.30)

Дисперсия X_i равна (см. формулу (1.23) §6)

D (X_i) = (0 – р)²·q + (1 – p)²·p =p·q (p +q) = pq.

Отсюда по теореме о дисперсии суммы

D(X)=npq. (1.31)

Задача 1. Стрелок делает по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий и вычислить математическое ожидание и дисперсию указанной случайной величины.

Решение. Случайная величина Х – число попаданий в мишень при 3-х выстрелах распределена по биноминальному закону, её возможные значения 0, 1, 2, 3.

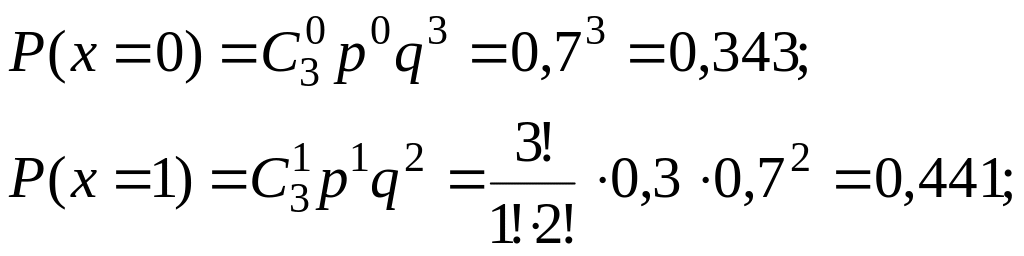
Ряд распределения случайной величины Х:

Х	0	1	2	3
р	0,343	0,441	0,189	0,027

2. Нормальный закон распределения

Среди законов распределения, которым подчиняются встречающиеся на практике случайные величины, чаще всего приходится иметь дело с нормальным законом распределения. В частности, нормальный закон распределения имеет фундаментальное значение при обработке результатов испытаний или эксперимента.

Функция нормального распределения

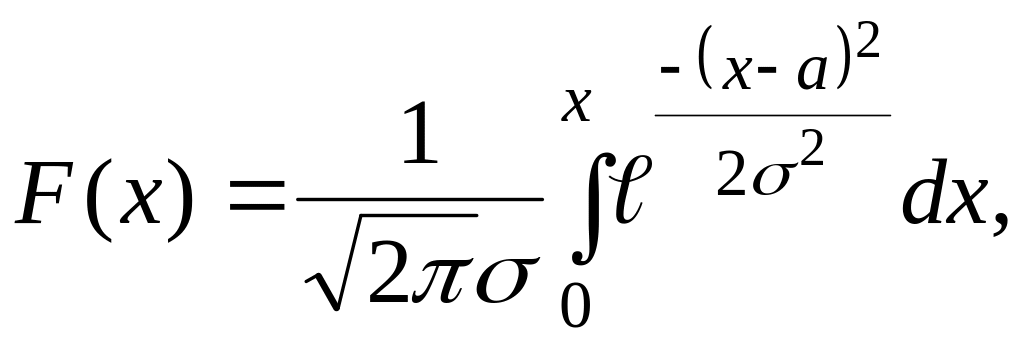(1.32)

где а и σ² – параметры распределения, представляющие собой соответственно математическое ожидание и дисперсию случайной величины х.

Графики функции нормального распределения для различных значений дисперсий и математического ожидания показаны на рис. 1.9.

Нормальная плотность вероятности

. (1.33)

На рис. 1.10 приведены графики нормальной плотности вероятностей для различных значений дисперсии и математического ожидания.

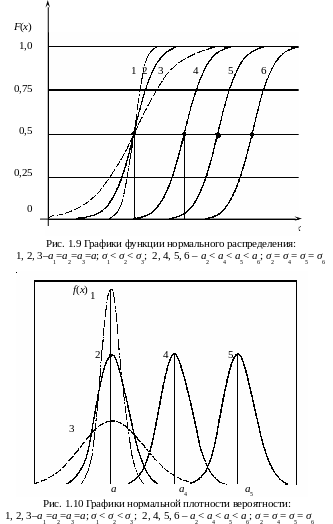
График нормальной плотности вероятности имеет максимальную ординату при х=а. Через эту же ординату проходит ось симметрии кривой. Поэтому у случайных величин, подчиняющихся нормальному закону распределения, значения математического ожидания, медианы и моды совпадают между собой.

Если в выражениях (1.32) и (1.33) перейти к новой переменной, называемой нормированной, случайной величиной,

, (1.34)

то получим

(1.35)

и

. (1.36)

Выражение (1.35) представляет собой функцию нормального закона распределения нормированной случайной величины (1.34) и называется нормированной функцией нормального распределения. Функция (1.36) является плотностью вероятности нормированного нормального распределения. Значения этой функции для различных z приведены в таблице прил.1. С нормальной плотностью вероятности (1.33) функция (1.36) имеет следующую связь:

. (1.37)

Выражения (1.35) и (1.36) показывают, что если случайная величина х распределена нормально со средним, равным а, и дисперсией, равной σ², то нормированная случайная величина z (1.34) также имеет нормальное распределение со средним, равным нулю, и дисперсией, равной единице.

Вероятность нахождения в интервале (–∞, х₁) случайной величины X, следующей нормальному закону распределения, на основании (1.16) и (1.32), определится как

, (1.38)

или, что легко доказать,

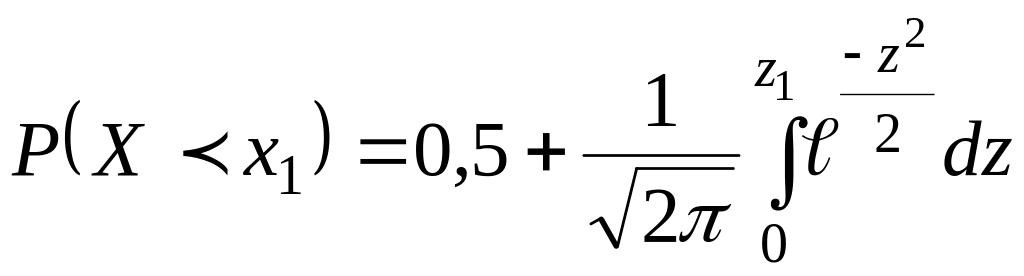. (1.39)

И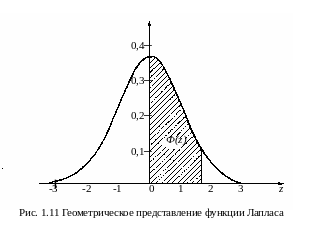 нтеграл с переменным верхним пределом вида

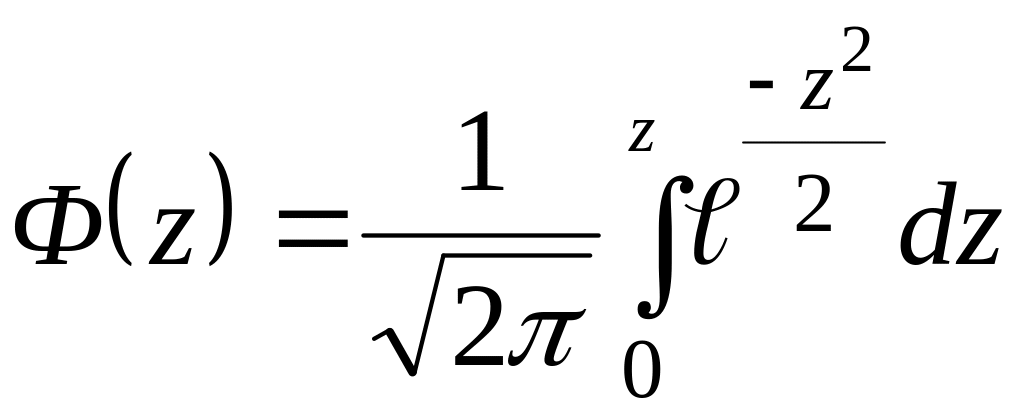. (1.40)

носит название функции Лапласа. Геометрически функция Лапласа представляет собой площадь под кривой φ(z) в промежутке от 0 до z (рис. 1.11). Значения этой функции приведены в таблице прил. 2.

Следует иметь в виду, что

Ф(–z) = – Ф(z), Ф(–∞) = –1/2, Ф(0)=0, Ф(∞) = 1/2. (1.41)

С учетом (1.37) вероятность нахождения в интервале (–∞; x₁) случайной величины Х определится из выражения

Р(Х<х₁)=0,5+Ф(z₁). (1.42)

Для интервала (x₁; х₂) соответствующую вероятность можно подсчитать на основании (1.32) и (1.37) как

Р(х₁<Х х₂)=Ф(z₂) – Ф(z₁), (1.43)

где

и . (1.44)

Пользуясь указанными соотношениями и таблицей прил. 2, легко можно определить, что вероятность попадания нормально распределенной случайной величины в интервал а ± σ составляет – P ≈ 0,68, в интервал а±2σ – ≈ 0,95 и в интервал а+3σ – P ≈ 0,997.

Нетрудно показать, что математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону, равны а

и σ² соответственно, т. е.

М(Х) = а, D(X) = σ².

Задача 2. Образцы из прессованного дюралюминиевого профиля испытывают на разрыв с целью определения предела прочности σ_в. Определить вероятность попадания значения предела прочности испытываемого образца в интервал (43 кгс/мм²; 47 кгс/мм²), если для случайной величины Х=σ_в, a=45,3кгc/мм² и σ =1,13 кгс/мм².

Решение. Пользуясь формулами (1.44), находим

и .

По таблице прил. 2 для вычисленных значений z₁и z₂ определяем:

Ф(z₁)=Ф(–2,03) = –Ф (2,03) = –0,4788

и

Ф(z₂) = Ф(1,50) = 0,4332.

На основании формулы (1.43) находим

Р(43 кгc/мм²<σ_в 47 кгс/мм²) =Ф(1,50) –Ф(–2,03) = 0,4332+0,4788=0,912.

Приведенные расчеты показывают, что если испытаниям на разрыв подвергнуть большое число образцов, то около 90% из них будут иметь значения предела прочности, лежащие в указанных интервалах.

Задача 3. Длина изготавливаемой автоматом детали представляет собой случайную величину, распределённую по нормальному закону с параметрами см; σ = 0,2 см. Найти вероятность брака, если допускаемые размеры детали должны быть см. Какую точность длины можно гарантировать вероятностью 0,97?

Решение. Остальные часто встречающиеся законы распределений случайных величин сведем в таблицу.

а) ,

т.к. параметр для нормального закона распределения.

(см. прил.1).

Вероятность брака

.

б) , (см. прил.2), т.к. .

Следовательно, с вероятностью 0,97 можно гарантировать размеры .