Задачи для самостоятельного решения

8.01. Совместное распределение случайных величин Х, Y задано таблицей

х y	-1	0	1
-1
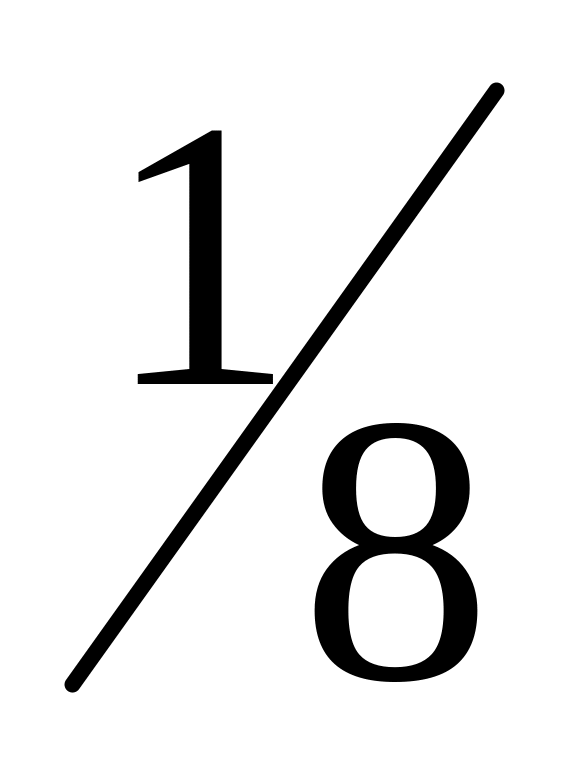
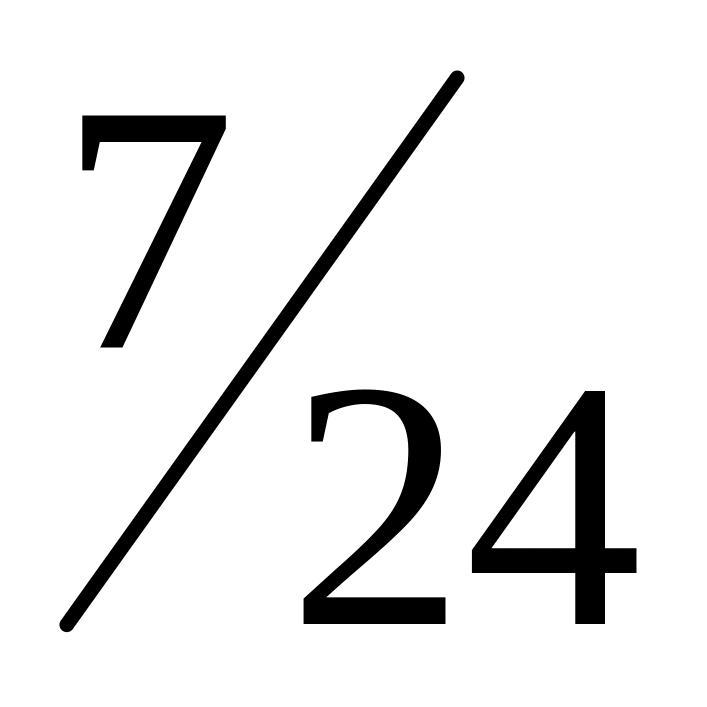
1

Найти ряды распределения для Х и Y. Будут ли независимы Х и Y?

8.02. Система случайных величин (Х, Y) подчинена закону распределения с плотностью:

Область D определяется неравенствами: , .

Найти:

1) коэффициент ;

2) математические ожидания и ;

3) средние квадратические отклонения , .

8.03. Дана таблица, определяющая закон распределения двух случайных величин (Х, Y):

х у	20	40	60
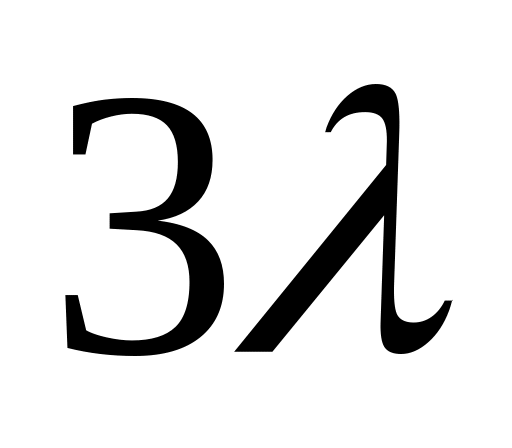
10			0
20
30

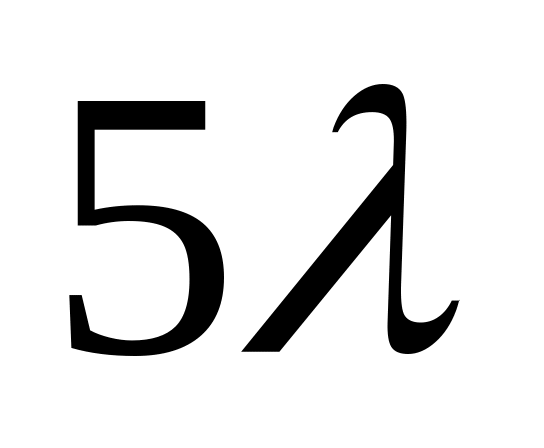
Найти:

1) коэффициент ;

2) математические ожидания и ;

3) дисперсии .

8.04. Дана плотность распределения вероятностей системы случайных величин, задаваемая функцией

.

Определить функцию совместного распределения системы (Х, Y), математические ожидания, дисперсии и коэффициент корреляции.

8.05. Независимые случайные величины Х, Y подчинены следующим законам распределения:

Написать выражение для функции распределения системы двух случайных величин (Х, Y).

8.06. Дана функция распределения случайных величин (Х, Y):

Определить, зависимы ли случайные величины Х и Y. Вычислить числовые характеристики .

8.07. Совместное распределение случайных величин Х, Y задано таблицей

у х	-1	0	1
-1
1

Найти ряды распределения для Х и Y.

8.08. По цели производится два независимых выстрела. Вероятность попадания в цель при первом выстреле равна , при втором – . Построить таблицу распределения системы двух случайных величин (Х,Y), где Х – число попаданий при первом выстреле, Y – число попаданий при втором выстреле.

8.09. Найти функцию распределения системы (Х, Y) из условия задачи 8.08.

8.10. Независимые случайные величины Х и Y подчинены законам распределения:

Написать выражение для функции распределения системы двух случайных величин.

8.11. Дана функция распределения системы двух случайных величин (Х, Y):

Найти плотность распределения вероятностей системы (Х, Y). Вычислить числовые характеристики .

8.12. Определить, зависимы ли случайные величины, из условия задачи 8.11. Найти для них числовые характеристики .

8.13. Система случайных величин (Х, Y) имеет плотность

.

Определить величину А. Найти функцию распределения . Определить вероятность попадания случайной точки (Х, Y) в область, заданную неравенствами .

8.14. Система двух случайных величин (Х, Y) подчинена закону равномерной плотности внутри прямоугольника:

.

Найти плотность распределения вероятности и вероятность попадания случайной точки (Х, Y) в квадрат со стороной , если центр этого квадрата совпадает с началом координат.

8.15. Плотность распределения вероятностей системы двух независимых случайных величин (Х, Y) задана выражением

.

Найти неизвестный параметр С и определить корреляционный момент.

8.16. Закон распределения системы двух случайных величин (Х,Y) задан таблицей распределения.

х у	0	1
-1	0,10	0,15
0	0,15	0,25
1	0,20	0,15

Найти следующие характеристики системы (Х, Y):

,

8.17. Случайные величины Х и Y независимы, и их плотности распределения вероятностей соответственно равны:

Определить функцию распределения системы случайных величин Х, Y. Найти числовые характеристики системы случайных величин (Х, Y).

8.18. Функция совместного распределения случайных величин Х и Y задана выражением

Определить, зависимы ли случайные величины Х и Y. Найти плотность распределения вероятностей системы (Х, Y).

8.19. Определить математические ожидания и дисперсии системы двух случайных величин (Х, Y), если плотность распределения вероятностей системы имеет следующий вид:

.

8.20. Случайная точка (Х, Y) имеет равномерное распределение внутри прямоугольника, ограниченного прямыми:

Найти функцию распределения системы случайных величин (Х,Y).

8.21. Система двух случайных величин (Х,Y) имеет плотность распределения вероятностей . Найти следующие числовые характеристики системы: ,

8.22. Система случайных величин (Х,Y) подчинена закону распределения с плотностью

Область D – квадрат, ограниченный прямыми:

Требуется:

1) определить коэффициент ;

2) вычислить вероятность попадания случайной точки (Х,Y) в квадрат Q, ограниченный прямыми:

8.23. Используя условия задачи 8.22, найти:

1) математические ожидания ;

2) средние квадратические отклонения

8.24. Система случайных величин (X,Y) подчинена закону распределения с плотностью

Область D определяется неравенствами:

, .

Найти:

1) коэффициент ;

2) математические ожидания .

8.25. Используя условия задачи 8.24, найти:

1) средние квадратические отклонения;

2) коэффициент корреляции .

69